Excelで偏相関を計算する方法
統計学では、 ピアソン相関係数を使用して2 つの変数間の線形関係を測定することがよくあります。ただし、場合によっては、 3 番目の変数を制御しながら2 つの変数間の関係を理解したい場合もあります。
たとえば、クラス内での生徒の現在の成績を管理しながら、生徒の学習時間数と最終試験の成績との関連性を測定したいとします。この場合、偏相関を使用して、学習時間と最終試験の成績との関係を測定できます。
このチュートリアルでは、Excel で偏相関を計算する方法を説明します。
例: Excel での偏相関
10 人の生徒に関する次の情報を表示するデータセットがあるとします。
- クラスの現在の学年
- 最終試験の勉強に費やした時間
- 最終試験のスコア
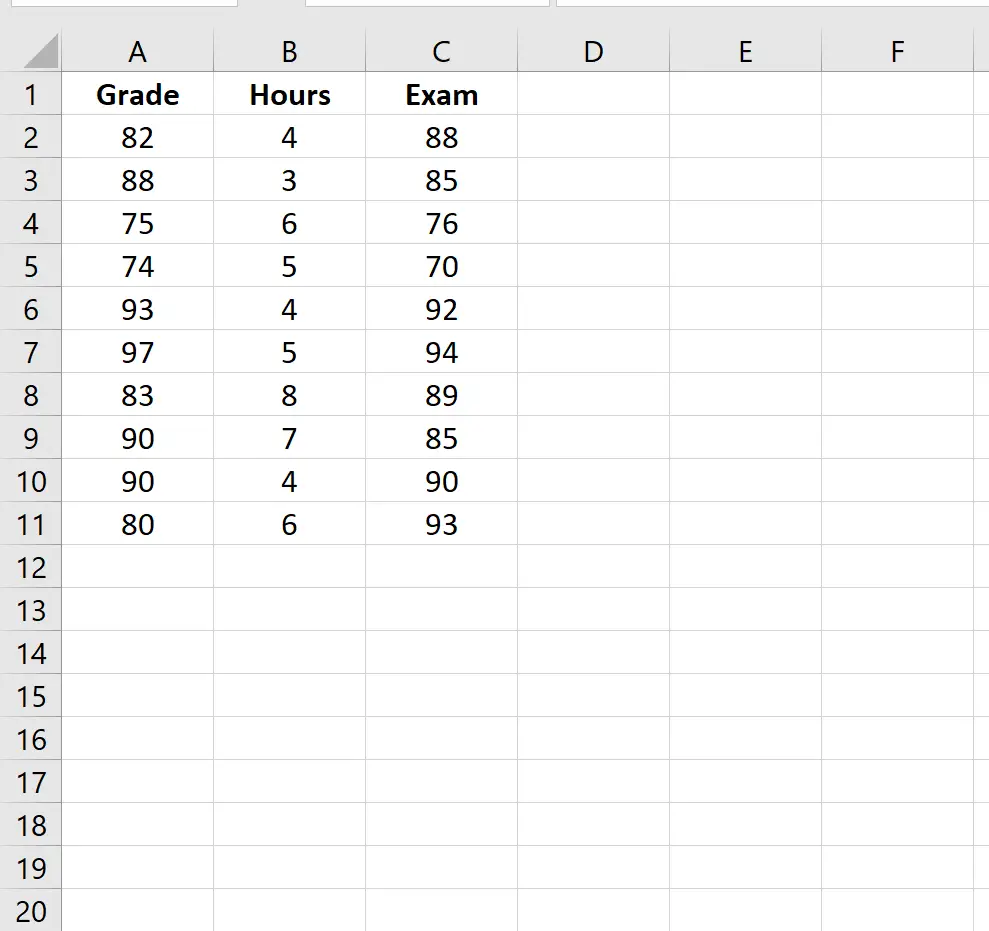
現在の成績を管理しながら、学習時間と試験の成績の間の偏相関を見つけるには、次の手順を使用します。
ステップ 1: 各ペアごとの相関を計算します。
まず、変数のペアごとの組み合わせ間の相関を計算します。
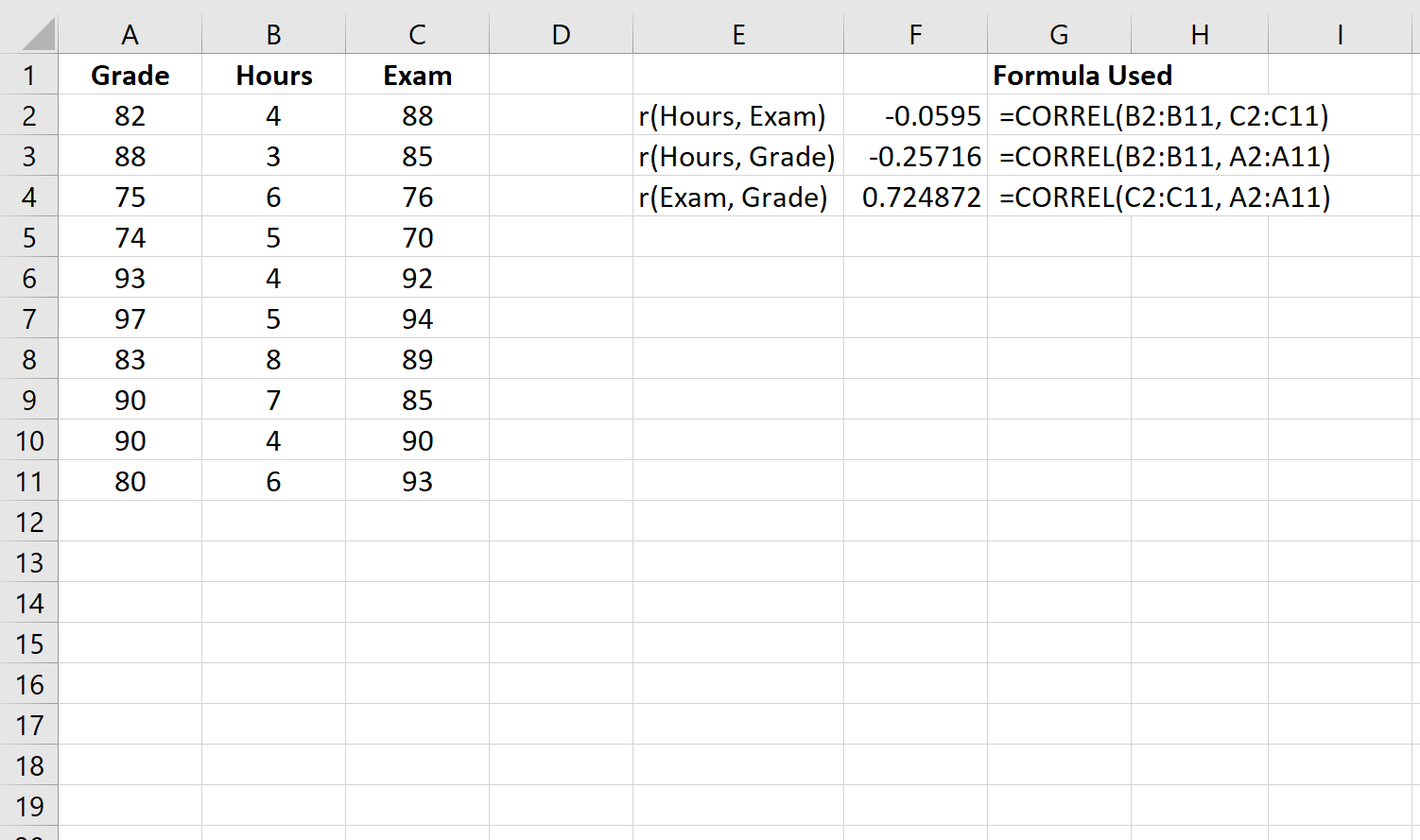
ステップ 2: 時間と試験スコアの間の偏相関を計算します。
変数 C を制御しながら変数 A と変数 B の間の偏相関を計算する式は次のとおりです。
偏相関 = (r A,B – r A,C *r B,C ) / √((1-r 2 A,B )(1-r 2 B,C ))
次のスクリーンショットは、この式を使用して、現在の成績を制御しながら時間数と試験の成績の間の偏相関を計算する方法を示しています。
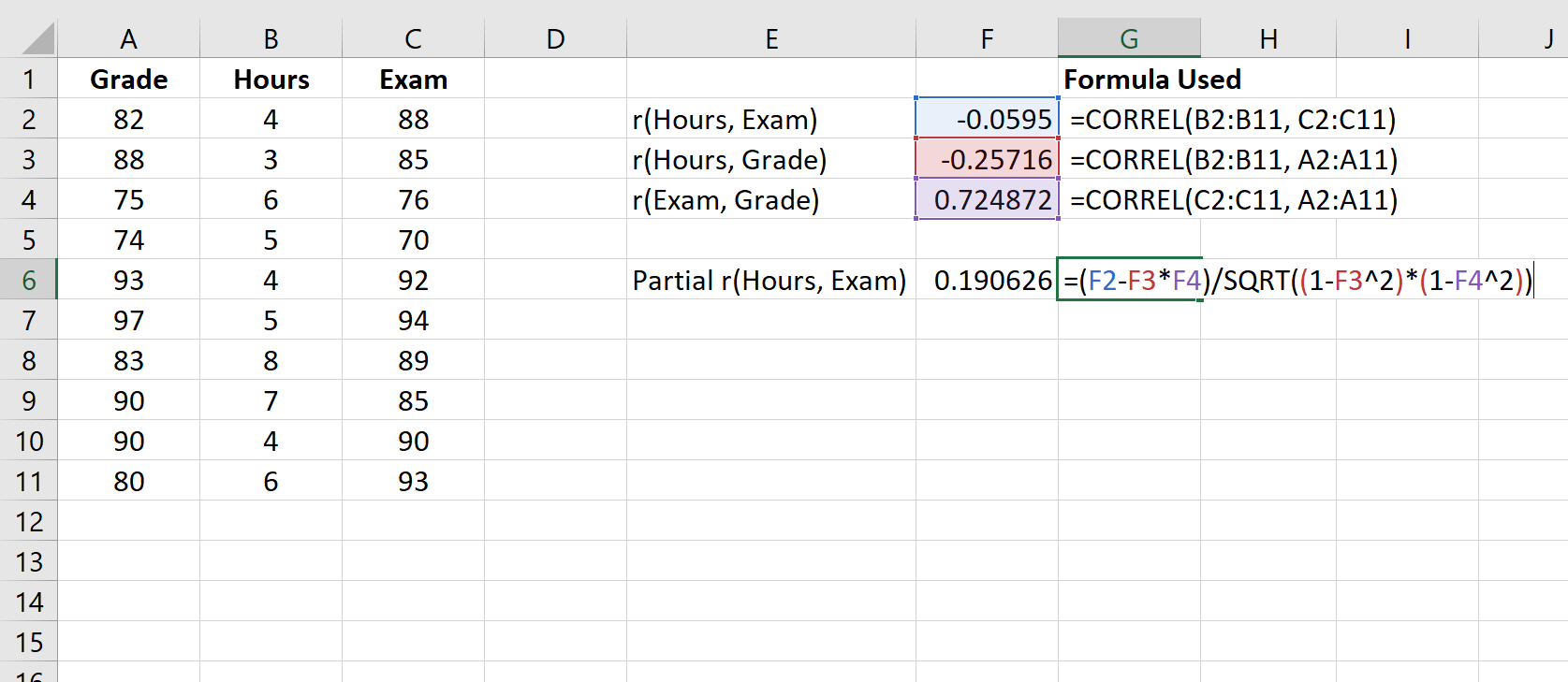
偏相関は0.190626です。この相関関係が統計的に有意であるかどうかを判断するには、対応する p 値を見つけることができます。
ステップ 3: 偏相関の p 値を計算します。
t検定統計量は次のように計算できます。
t = r√(n-3) / √(1-r 2 )
次のスクリーンショットは、この式を使用して検定統計量と対応する p 値を計算する方法を示しています。
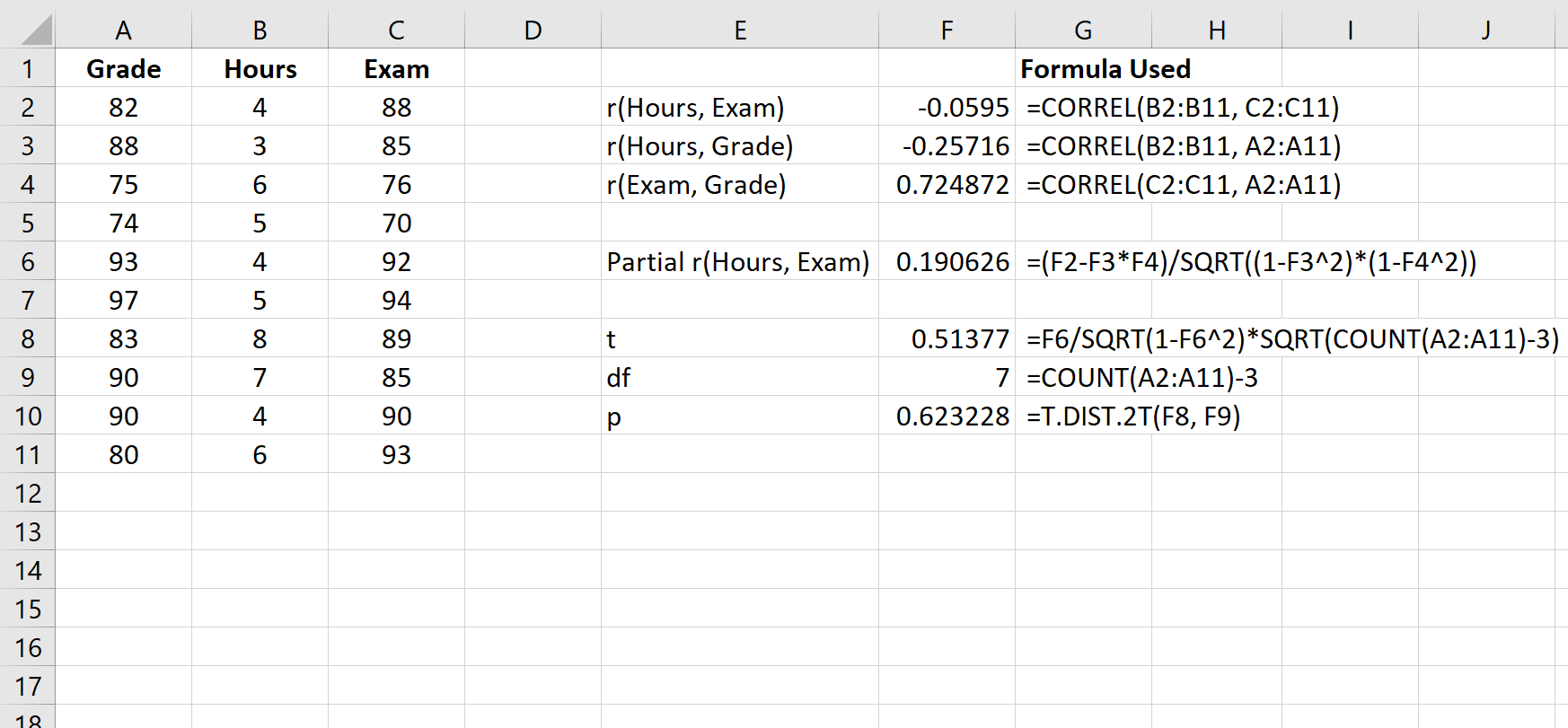
t検定統計量は0.51377です。自由度の合計は n-3 = 10-3 = 7です。対応する p 値は0.623228です。この値は 0.05 未満ではないため、時間と試験結果の間の偏相関が統計的に有意ではないことを意味します。