共分散行列の読み方

によるベンジャミン・アンダーソン博士 7月 10, 2023 ガイド 0コメント

共分散は、 1 つの変数の変化が 2 番目の変数の変化とどのように関連しているかを示す尺度です。より具体的には、これは 2 つの変数が線形に関連している程度の尺度です。

共分散行列は、多くの異なる変数間の共分散を示す正方行列です。これは、データセット内でさまざまな変数がどのように関連しているかを理解するのに役立ちます。

次の例は、実際に共分散行列を読み取る方法を示しています。

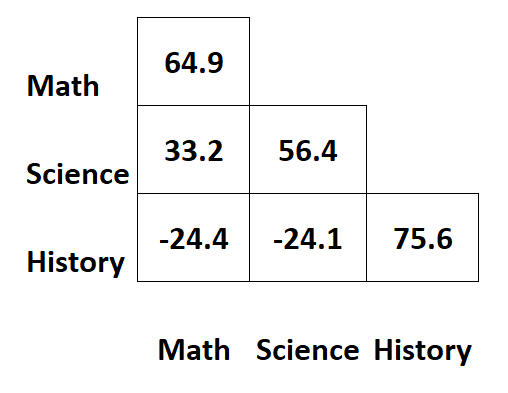
学生の 3 つの異なる科目の試験得点に関する情報を含む次の共分散行列があるとします。

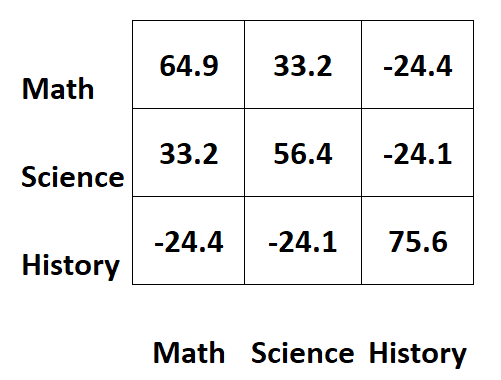
マトリックスの対角に沿った値は、各被験者の分散を表します。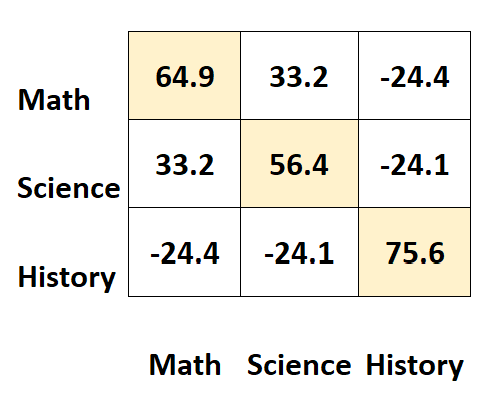

例えば：

行列の他の値は、異なる被験者間の共分散を表します。

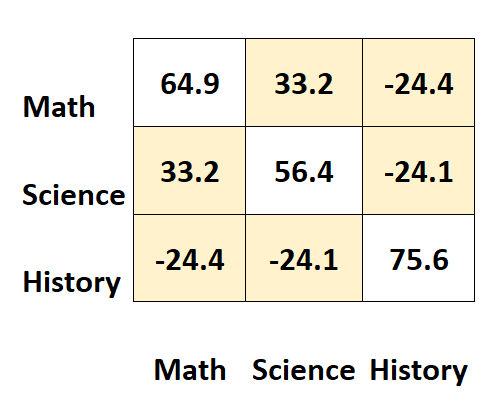
例えば：

共分散の正の数は、 2 つの変数が並行して増加または減少する傾向があることを示します。

たとえば、数学と科学には正の共分散 ( 33.2 ) があり、数学の得点が高い生徒は科学の得点も高い傾向があることを示しています。

逆に、数学の成績が悪い生徒は、科学の成績も悪い傾向があります。

共分散の負の値は、 1 つの変数が増加すると、2 番目の変数が減少する傾向があることを示します。

たとえば、数学と歴史には負の共分散 ( -24.44 ) があり、数学の成績が高い生徒は歴史の成績が低い傾向があることを示しています。

逆に、数学の得点が低い生徒は歴史の得点が高くなる傾向があります。

共分散行列の対称性に関するメモ

共分散行列は完全に対称であることに注意してください。

たとえば、右上のセルには左下のセルとまったく同じ値が表示されます。

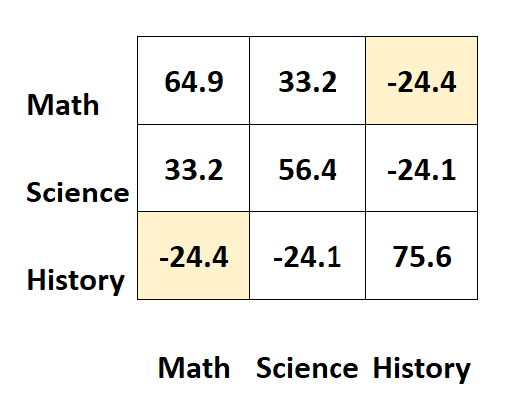
実際、2 つのセルは歴史と数学の間の共分散を測定します。

共分散行列は対称であるため、行列に表示される共分散値の半分は冗長で不要です。

したがって、共分散行列の半分しか表示されない場合があります。

実際には、共分散行列よりも相関行列の作成と解釈が必要になることがよくあります。

ただし、共分散行列は、さまざまな機械学習アルゴリズムやモデルの「内部で」使用されることがよくあります。

たとえば、共分散行列は主成分分析中に使用され、多数の変数を含むデータセットの基礎となるパターンを理解するのに役立ちます。

次のチュートリアルでは、さまざまな統計ソフトウェアを使用して共分散行列を作成する方法を説明します。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る