Stata で分位点回帰を実行する方法
線形回帰は、1 つ以上の説明変数と応答変数の間の関係を理解するために使用できる方法です。
通常、線形回帰を実行するときは、説明変数の値に基づいて応答変数の平均値を推定する必要があります。しかし代わりに、中央値、0.25 パーセンタイル、0.90 パーセンタイル、またはその他の必要なパーセンタイルを推定することもできます。
ここで分位回帰が登場します。線形常回帰と同様に、分位回帰では、説明変数の値に基づいて応答変数の特定の値 (中央値、0.25 パーセンタイル、0.90 パーセンタイルなど) を予測する回帰式が作成されます。
このチュートリアルでは、Stata で分位点回帰を実行する方法について説明します。
例: Stata の分位点回帰
この例では、 autoという組み込みの Stata データセットを使用します。まず、予測変数として重みを使用し、応答変数として mpg を使用して線形回帰モデルを近似します。これにより、車の重量に基づいて、車の平均予想燃費がわかります。次に、分位点回帰モデルを当てはめて、車の重量に基づいて 0.90 mpg パーセンタイルを予測します。
ステップ 1: データをロードして表示します。
次のコマンドを使用してデータをロードします。
システムの自動使用
次のコマンドを使用して、mpg 変数と Weight 変数の概要を取得します。
mpg重量を合計する

ステップ 2: 単純な線形回帰を実行します。
次のコマンドを使用して、重みを説明変数として、mpg を応答変数として使用して単純な線形回帰を実行します。
重量をmpgに回帰する
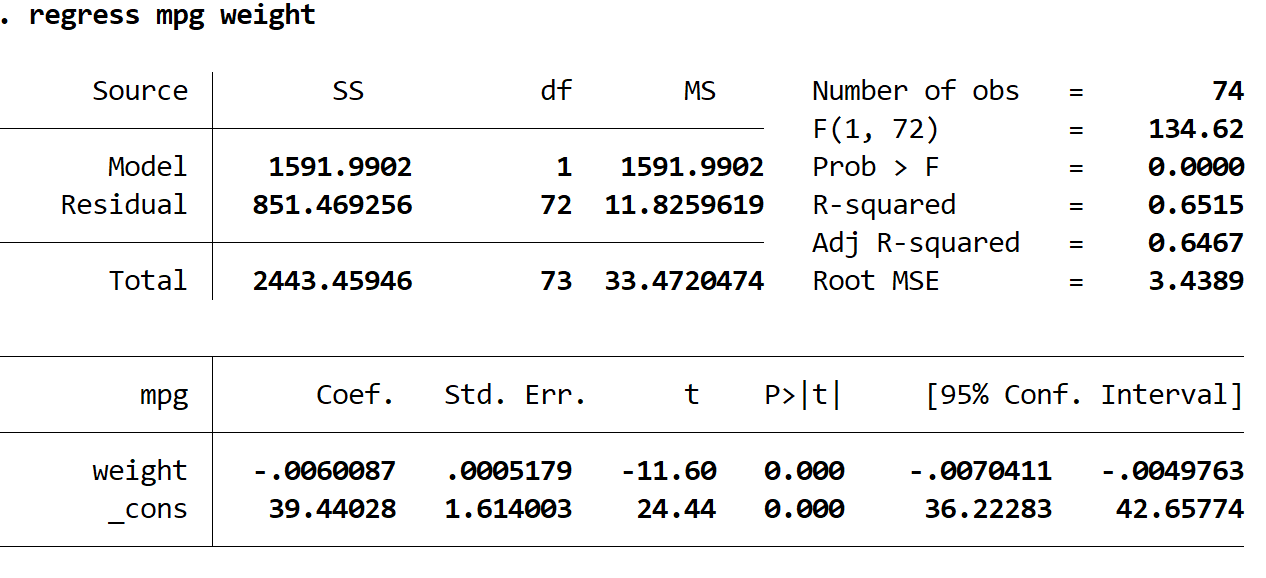
出力テーブルから、推定された回帰式は次のとおりであることがわかります。
予測mpg = 39.44028 – 0.0060087*(重量)
この式を使用して、車の重量を考慮して、車の推定平均mpg を求めることができます。たとえば、重量が 4,000 ポンドの車の燃費は 15,405 mpg と推定されます。
予測mpg = 39.44028 – 0.0060087*(4000) = 15.405
ステップ 3: 分位点回帰を実行します。
次に、分位点回帰を実行して、車の重量に基づいて、車の燃費の推定90パーセンタイルを取得しましょう。
この分位点回帰を実行するには、 qregコマンドにquantile(0.90)を指定して使用します。
重量 qreg mpg、分位数 (0.90)
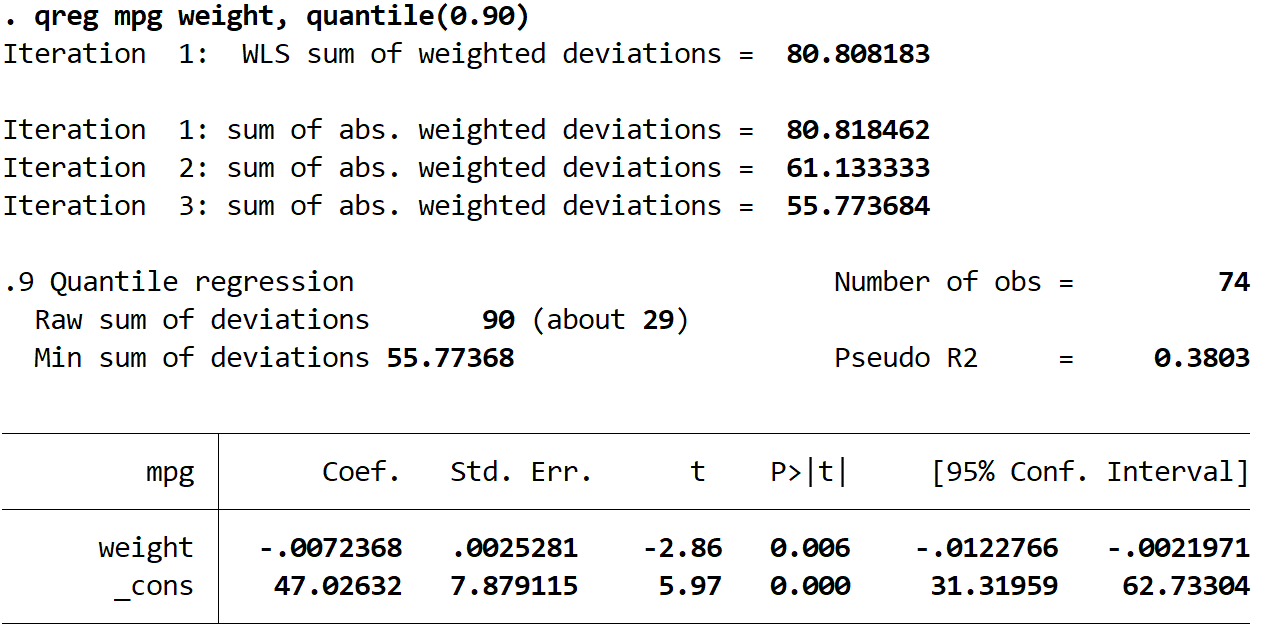
出力テーブルから、推定された回帰式は次のとおりであることがわかります。
90パーセンタイルの予測 mpg = 47.02632 – 0.0072368*(重量)
この方程式を使用して推定値を見つけることができます 車の重量を考慮した90パーセンタイルの自動車の mpg。たとえば、重量 4,000 ポンドの車の90パーセンタイル mpg は、18,709 と推定されます。
90パーセンタイルの予測 mpg = 47.02632 – 0.0072368*(4,000) = 18.079
以前の線形回帰モデルでは、重量 4,000 ポンドの車の推定平均燃費は 15,405 mpg であることが示されたことを思い出してください。したがって、この分位回帰モデルから、重量 4,000 ポンドの車が、その特定の重量のすべての車の90パーセンタイルに入るには、 18,079 mpg を獲得する必要があることがわかります。
Stata で一度に複数の分位点回帰を実行
Stata では複数の分位点回帰を一度に実行することもできます。たとえば、 25パーセンタイル、中央値 (たとえば、 50パーセンタイル)、および90パーセンタイルを同時に推定するとします。
これを行うには、 sqregコマンドとq()コマンドを使用して、推定する分位数を指定します。
重量 mpg sqreg、q (0.25、0.50、0.90)
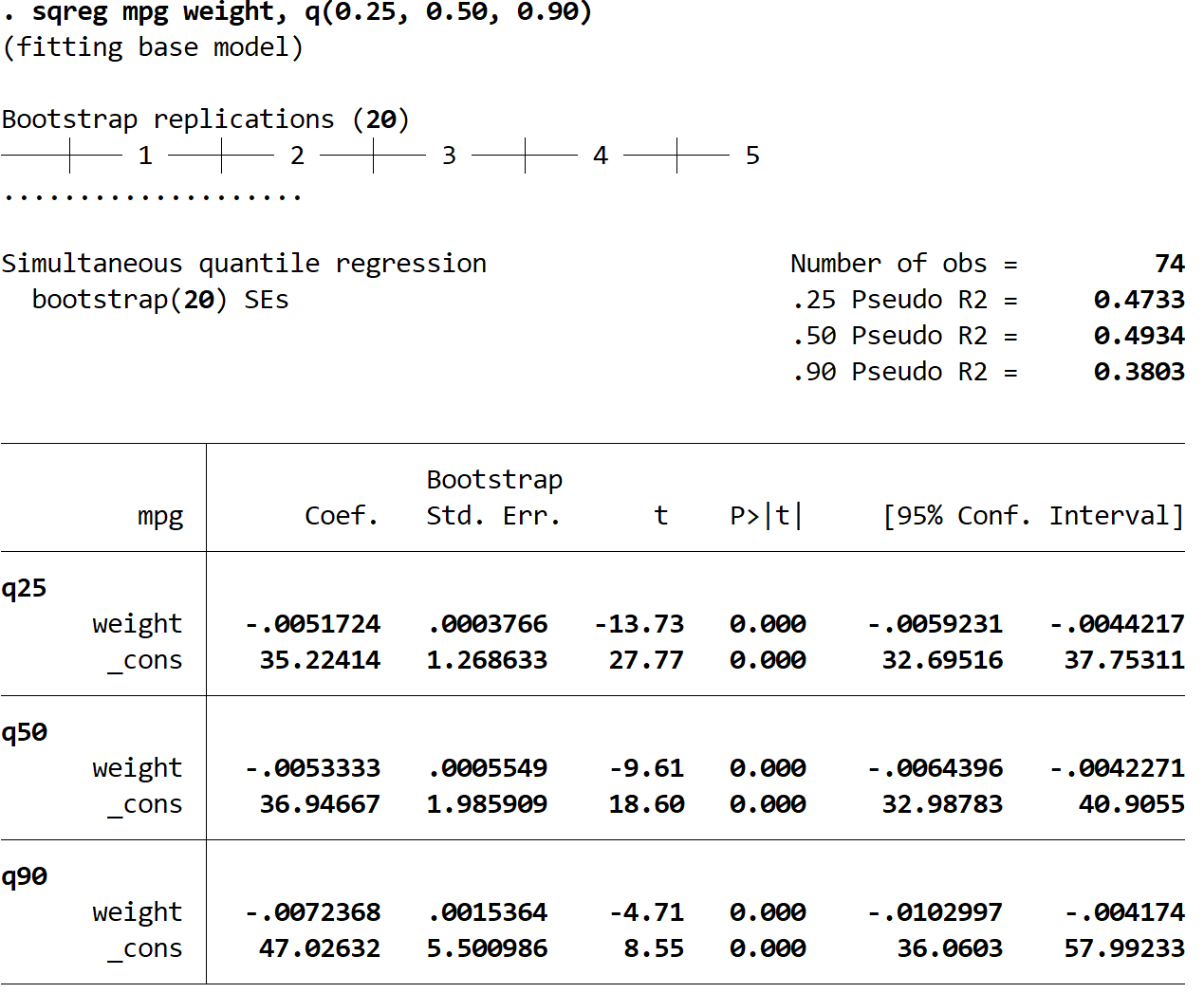
この結果を使用して、各分位回帰の推定回帰式を構築できます。
(1) 25パーセンタイルの予測 mpg = 35.22414 – 0.0051724*(重量)
(2) 50パーセンタイルの予測 mpg = 36.94667 – 0.0053333*(重量)
(3) 90パーセンタイルの予測 mpg = 47.02632 – 0.0072368*(重量)