サンプルサイズが等しくない場合に分散分析を実行する方法

統計に関して学生がよく尋ねる質問は次のとおりです。

各グループのサンプルサイズが等しくない場合、一元配置分散分析を実行できますか?

短い答え:

はい、サンプルサイズが等しくない場合でも、一元配置分散分析を実行できます。サンプルサイズが等しいということは、ANOVA で行われる仮定の 1 つではありません。

ただし、サンプル サイズが等しくない場合に一元配置分散分析を実行する場合は、考慮すべき 2 つの潜在的な問題があります。

(1)統計的検出力の低下。

(2)ロバスト性は不等分散に還元されます。

次のセクションでは、これら 2 つの潜在的な問題について詳しく説明します。

問題 #1: 統計的検出力の低下

グループを比較するために任意のタイプの統計検定を使用する場合、各グループのサンプル サイズが等しい場合に検定の統計検出力が最も高くなります。

統計的検出力とは、効果が実際に存在する場合に、テストでその効果が検出される確率を指すことを思い出してください。

グループ間のサンプル サイズの差が大きいほど、ANOVA の統計検出力が低くなることがわかります。

このため、研究者は一般に、検出力を高め、真の違いを検出する可能性を高めるために、サンプルサイズが等しいことを望んでいます。

確かにサンプルサイズが等しくない一元配置分散分析を実行することは可能ですが、一元配置分散分析の検出力が低下することに注意する必要があります。

問題 #2: ロバスト性が不等分散にまで低下する

一元配置分散分析の前提の 1 つは、各グループ間の分散が等しいということです。

一般に、一元配置分散分析は等分散仮定の違反に対して堅牢であると考えられますが、これは各グループのサンプル サイズが同じ場合に限られます。

したがって、グループ間のサンプルサイズや分散が等しくない場合、一元配置分散分析の結果を信頼するのは困難になる可能性があります。

サンプルサイズが等しくない場合に一元配置分散分析を使用するかどうかを決定する方法

サンプルサイズが等しくなく、一元配置分散分析を実行してグループ平均間の差異を検定する場合は、次のフローチャートを使用して続行方法を決定できます。

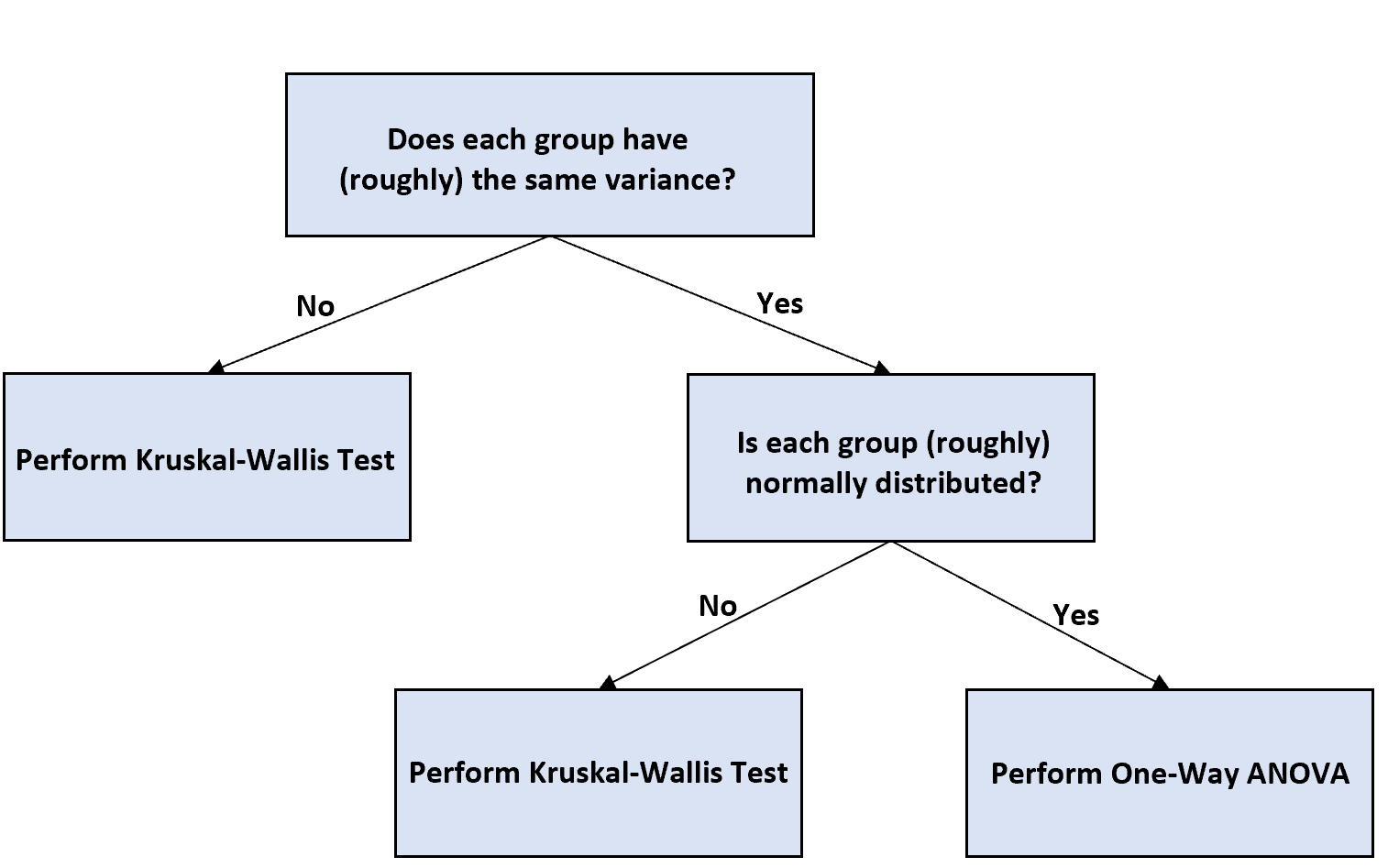
フローチャートの簡単な説明は次のとおりです。

ステップ 1: 各グループの分散が同じかどうかを判断します。

各グループの分散が同じかどうかを判断するには、次の 2 つのアプローチのいずれかを使用できます。

• 各グループの箱ひげ図を作成し、各グループの値の分布がほぼ等しいかどうかを確認します。
• Bartlett 検定のような等分散に対する正式な統計検定を実行します。

分散が等しくない場合は、一元配置分散分析と同等のノンパラメトリックとみなされているクラスカル・ウォリス検定を実行します。

ギャップが等しい場合は、次のステップに進みます。

ステップ 2: 各グループが正規分布しているかどうかを判断します。

各グループの値がほぼ正規分布しているかどうかを判断するには、次の 2 つのアプローチのいずれかを使用できます。

• 各グループのヒストグラムまたはQQ プロットを作成します。
• Shapiro-Wilk、Kolmogorov-Smironov、Jarque-Barre、D’Agostino-Pearson などの正式な統計検定を実行します。

各グループが正規分布している場合は、通常の一元配置分散分析と同様に一元配置分散分析を実行し、結果を解釈できます。

各グループが正規分布していない場合は、代わりにクラスカル-ウォリス検定を実行します。

追加リソース

一元配置分散分析の概要
ANOVA の仮定を確認する方法
クラスカル・ウォリス検定の概要
ANOVA での F 値と P 値の解釈方法