完全ガイド: anova 結果を報告する方法

一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

一元配置分散分析の結果を報告するときは、常に次の一般的な構造を使用します。

• 独立変数と従属変数の簡単な説明。
• ANOVA の全体的な F 値と対応する p 値。
• 事後比較の結果 (p 値が統計的に有意な場合)。

使用できる正確な表現は次のとおりです。

[従属変数]に対する[独立変数]の影響を比較するために、一元配置分散分析が実行されました。

一元配置分散分析により、少なくとも 2 つのグループ間で [従属変数] に統計的に有意な差があることが明らかになりました (F (グループ間 df、グループ df 内) = [F 値]、p = [p -価値]）。

多重比較のための Tukey の HSD 検定により、[従属変数] の平均値が [グループ名] と [グループ名] の間で有意に異なることが明らかになりました (p = [p 値]、95% CI = [低い、優れた])。

[グループ名] と [グループ名] の間に統計的に有意な差はありませんでした (p = [p 値])。

次の例は、実際に一元配置分散分析の結果をレポートする方法を示しています。

例: 一元配置分散分析の結果のレポート

研究者が研究に参加する 30 人の学生を募集するとします。学生は、翌月に試験の準備のために 3 つの学習テクニックのうち 1 つを使用するようにランダムに割り当てられます。月末に、生徒全員が同じテストを受けます。

次に、研究者は一元配置分散分析を実行して、3 つのグループ間で試験の平均点に差があるかどうかを判断します。

次の表は、一元配置分散分析の結果と Tukey の事後多重比較表を示しています。

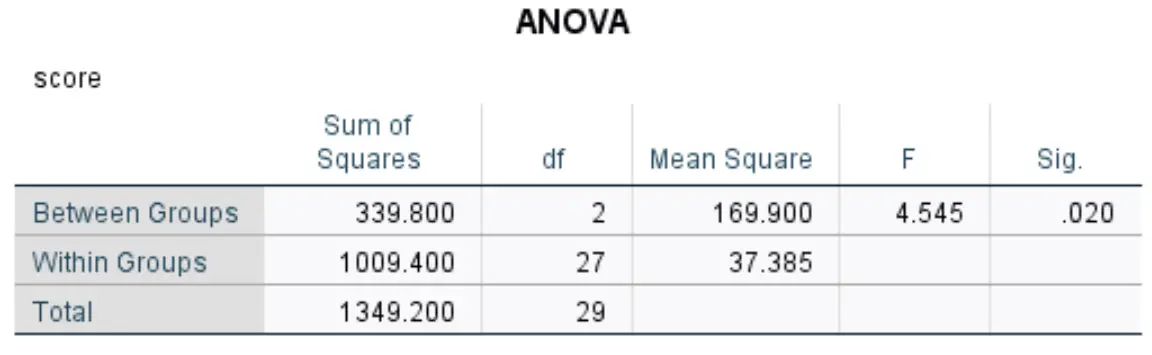
一元配置分散分析結果をレポートする方法は次のとおりです。

検査結果に対する 3 つの異なる研究手法の影響を比較するために、一元配置 ANOVA が実行されました。

一元配置分散分析により、少なくとも 2 つのグループ間で試験の平均得点に統計的に有意な差があることが明らかになりました (F(2,27) = [4.545]、p = 0.02)。

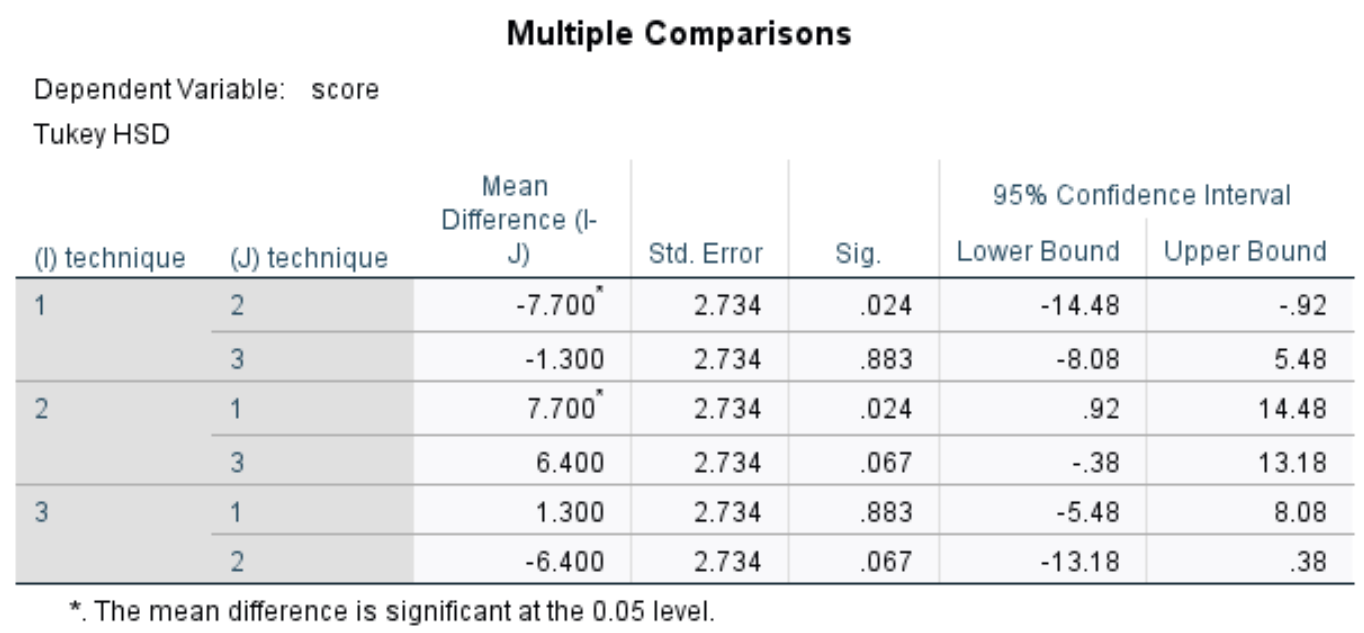
多重比較のための Tukey の HSD テストにより、試験スコアの平均値が技術 1 と技術 2 の間で有意に異なることが明らかになりました (p = 0.024、95% CI = [-14.48、-0.92])。

テクニック 1 とテクニック 3 の間 (p = 0.883)、またはテクニック 2 とテクニック 3 の間 (p = 0.067) で、平均試験スコアに統計的に有意な差はありませんでした。

留意すべき事項

一元配置分散分析の結果を報告する際に留意すべき点がいくつかあります。

記述統計テーブルを使用します。

読者にデータのより完全な全体像を与えるために、各治療グループの値の平均と標準偏差も示す記述統計の表を提示すると役立つ場合があります。

たとえば、SPSS は、3 つの学習スキル グループごとに生徒の試験得点の平均と標準偏差を示す次の記述統計表を作成します。

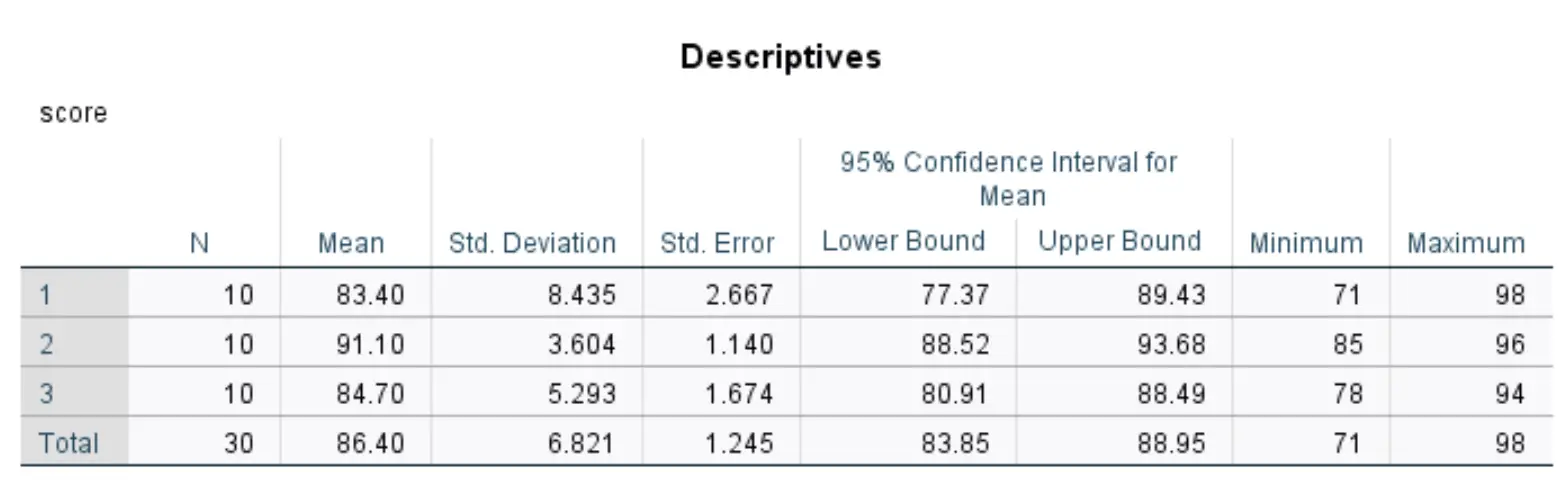
必要な場合にのみ事後結果を報告してください。

ANOVA の全体的な p 値が統計的に有意でない場合は、グループ間の事後多重比較は実行しません。これは、最終レポートで事後結果を報告する必要がないことは明らかです。

事後テストを実行する必要がある場合は、Tukey HSD テストが最も一般的に使用されますが、代わりにScheffe テストまたは Bonferroni テストを使用できる場合もあります。

必要に応じて p 値を丸めます。

通常、分散分析結果の全体の F 値とすべての p 値は、簡潔にするために小数点以下 2 桁または 3 桁に四捨五入されます。

使用する小数点以下の桁数に関係なく、レポート全体で一貫性を保つようにしてください。

追加リソース

次のチュートリアルでは、APA 形式で他の統計テストと手順をレポートする方法について説明します。

二元配置分散分析結果をレポートする方法 (例付き)
クロンバックのアルファを報告する方法 (例付き)
t 検定結果を報告する方法: 例付き
カイ二乗結果を報告する方法: 例付き
ピアソン相関関係をレポートする方法: 例付き
回帰結果を報告する方法: 例付き