分類ツリーと回帰ツリーの概要
一連の予測変数と応答変数の間の関係が線形の場合、重線形回帰などの方法で正確な予測モデルを生成できます。
ただし、一連の予測変数と応答の間の関係が高度に非線形で複雑な場合は、非線形手法の方がパフォーマンスが向上する可能性があります。
非線形手法の例としては、分類および回帰ツリー(CART と略されることが多い) があります。
名前が示すように、CART モデルは一連の予測変数を使用して、応答変数の値を予測する決定木を作成します。
たとえば、数百人のプロ野球選手の予測変数「プレー年数」と「平均ホームラン数」と応答変数「年俸」を含むデータセットがあるとします。
このデータセットの回帰ツリーは次のようになります。
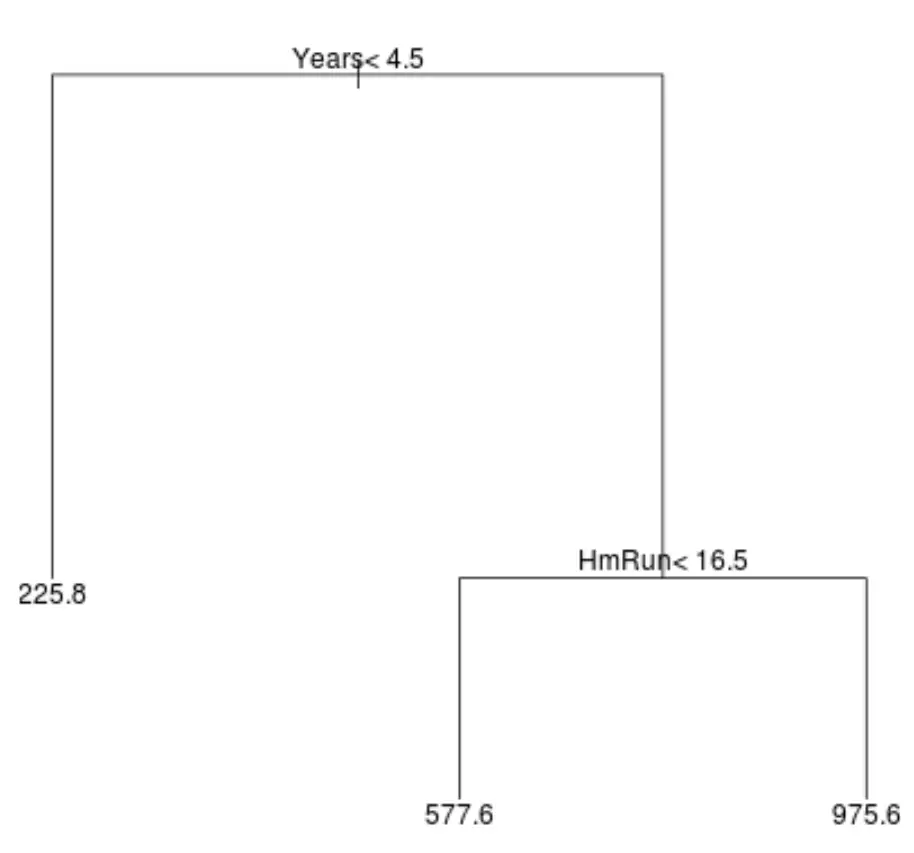
ツリーを解釈する方法は次のとおりです。
- プレー歴が4年半未満の選手の予想年俸は22万5,000ドルだ。
- 4年半以上プレーし、平均本塁打16.5本未満の選手の予想年俸は57万7,000ドルだ。
- 4年半以上の選手経験と平均16.5本塁打以上の選手の予想年俸は97万5,600ドルです。
このモデルの結果は直感的に理解できるはずです。経験年数が長く、平均ホームラン数が多い選手ほど、給与が高くなる傾向があります。
このモデルを使用して、新しいプレーヤーの年俸を予測できます。
たとえば、ある選手が 8 年間プレーし、年間平均 10 本塁打を打ったとします。私たちのモデルによると、このプレーヤーの年俸は 577,600 ドルであると予測されます。
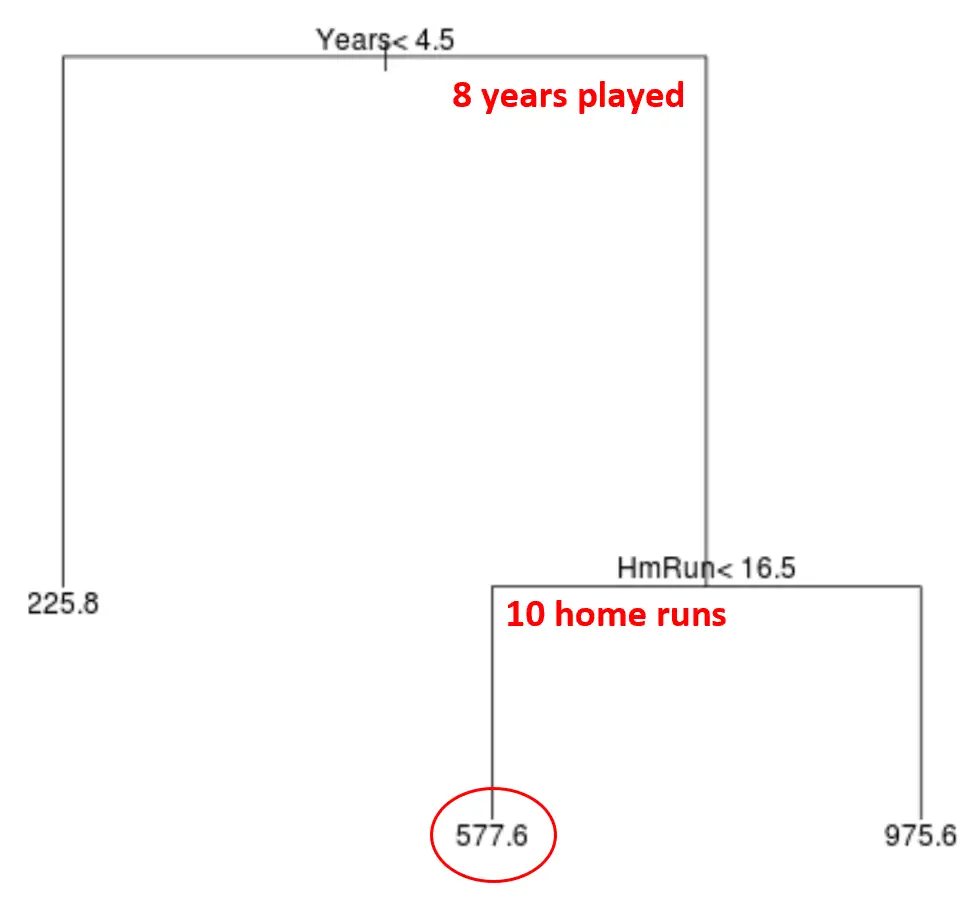
ツリーに関するいくつかのコメント:
- ツリーの最上位にある最初の予測変数が最も重要です。つまり、応答変数の値の予測に最も影響を与える変数です。この場合、出場年数はサーキットの平均よりも年俸を正確に予測します。
- ツリーの下部の領域はリーフ ノードと呼ばれます。この特定のツリーには 3 つの終端ノードがあります。
CART モデルを作成する手順
次の手順を使用して、特定のデータセットの CART モデルを作成できます。
ステップ 1: 再帰的バイナリ分割を使用して、トレーニング データ上に大きなツリーを成長させます。
まず、再帰的バイナリ分割と呼ばれる貪欲なアルゴリズムを使用して、次の方法で回帰木を成長させます。
- すべての予測変数 (X 1 、 X 2 、…、残差標準誤差) が最小であると考えます。 。
- 分類ツリーの場合、結果として得られるツリーの分類エラー率が最も低くなるように予測子とカットポイントを選択します。
- このプロセスを繰り返し、各ターミナル ノードの観測値が特定の最小数を下回った場合にのみ停止します。
このアルゴリズムは、ツリー構築プロセスの各ステップで、将来を見据えて将来の段階でより良いツリー グローバルにつながる分割を選択するのではなく、そのステップのみに基づいて最適な分割を決定するため、貪欲です。
ステップ 2: α に基づいて、コスト複雑性枝刈りを大きなツリーに適用して、最適なツリーのシーケンスを取得します。
大きな木を成長させたら、次のように複雑な剪定と呼ばれる方法を使用してそれを剪定する必要があります。
- T 個の終端ノードを持つ考えられるツリーごとに、RSS + α|T| を最小化するツリーを見つけます。
- α の値を増やすと、より多くの終端ノードを持つツリーにペナルティが課されることに注意してください。これにより、ツリーが複雑になりすぎないようにすることができます。
このプロセスにより、α の値ごとに最適なツリーのシーケンスが生成されます。
ステップ 3: k 分割交差検証を使用して α を選択します。
α の各値に最適なツリーを見つけたら、k 分割相互検証を適用して、テスト誤差を最小限に抑える α の値を選択できます。
ステップ 4: 最終的なテンプレートを選択します。
最後に、選択した α の値に対応する最終モデルを選択します。
CARTモデルの長所と短所
CART モデルには次の利点があります。
- 解釈は簡単です。
- 説明するのは簡単です。
- それらは簡単に視覚化できます。
- これらは回帰問題と分類問題の両方に適用できます。
ただし、CART モデルには次の欠点があります。
- 他の非線形機械学習アルゴリズムほど予測精度が高くない傾向があります。ただし、バギング、ブースティング、ランダム フォレストなどの方法を使用して多くのデシジョン ツリーをクラスタリングすることにより、予測精度を向上させることができます。