加算ルール（または加算ルール）

によるベンジャミン・アンダーソン博士 8月 1, 2023 確率 0コメント

この記事では、加算の法則とも呼ばれる加算の法則とは何か、また確率や統計でどのように使用されるのかについて説明します。さらに、加算ルールの公式が何であるかを確認し、その使用方法を示す演習を解くことができます。

足し算の法則（または足し算の法則）とは何ですか？

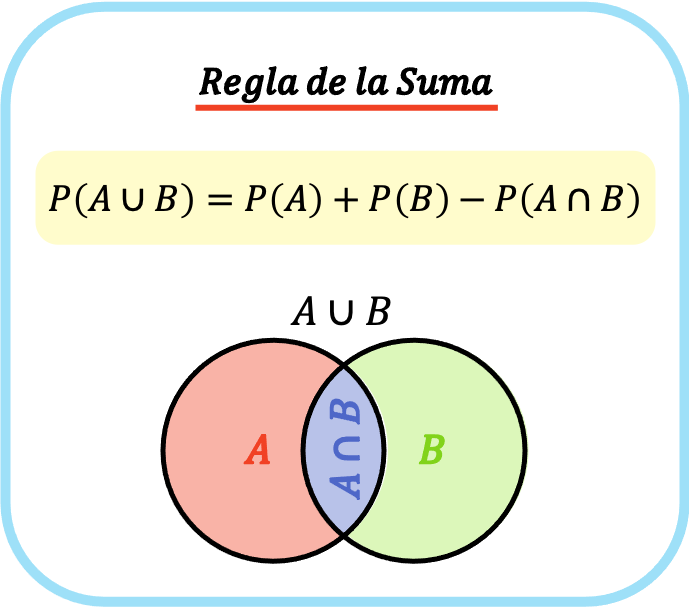
加算規則(または加算規則) は、2 つのイベントの確率の合計が、別々に発生する各イベントの確率の合計から両方のイベントが同時に発生する確率を引いたものに等しいと規定します。

したがって、加算ルールの式は P(A⋃B)=P(A)+P(B)−P(A⋂B) となります。

したがって、2 つの確率を加算するには、2 つの事象の同時確率を表す項も減算する必要があるため、各確率を単純に加算することはできません。ただし、場合によっては、各事象の確率を加算することによってのみ、確率の合計の正しい結果を得ることができます。以下では、これらのケースがどのようなものであるかを見ていきます。

つまり、加算ルールは、1 つまたは別のイベントが発生する確率、つまり 2 つの可能なイベントのうちの少なくとも 1 つが発生する確率を計算するために使用されます。

加算ルールの式

加算の法則では、イベント A またはイベント B が発生する確率を計算するには、イベント A が発生する確率とイベント B が発生する確率を加算し、両方のイベントが同時に発生する確率を減算する必要があると述べています。。

したがって、加算ルール (または加算ルール) の式は次のようになります。

金：

$P(A\cup B)$

イベント A またはイベント B の確率です。
$P(A)$

はイベント A が発生する確率です。
$P(B)$

はイベント B が発生する確率です。
$P(A\cap B)$

はイベント A とイベント B が発生する同時確率です。

したがって、合計ルールを使用するには、2 つのイベントの結合確率を計算する方法を知る必要があります。これがどのように行われるかは、次のリンクで確認できます。

➤参照:同時確率の計算方法

排他的イベントの合計ルールの例

概念の理解を終えるために、加算ルールを適用する方法の例を見てみましょう。

青いボール10個、オレンジのボール6個、緑色のボール4個を箱に入れました。青またはオレンジのボールを引く確率はどれくらいですか?

この演習では、あるイベントまたは別のイベントが発生する確率を決定するように求められます。したがって、問題を解決するには、次の加算規則公式を使用する必要があります。

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

したがって、最初にラプラスの法則を使用して、各イベントが個別に発生する確率を計算します。

$P(\text{bola azul})=\cfrac{10}{10+6+4}=0,5$

$P(\text{bola naranja})=\cfrac{6}{10+6+4}=0,3$

ただし、この場合、イベントは 2 つの相互に排他的なイベントであるため、両方のイベントを同時に発生させることはできません。したがって、青いボールを描くとオレンジ色のボールを描くことはできなくなり、その逆も同様です。

したがって、両方のイベントの同時確率はゼロであるため、合計ルールの式は次のように簡略化されます。

$P(A\cup B)=P(A)+P(B)-\cancelto{0}{P(A\cap B)}$

したがって、青いボールまたはオレンジ色のボールをキャッチする確率の計算は次のようになります。

$\begin{aligned}P(\text{bola azul}\cup \text{bola naranja})&=P(\text{bola azul})+P(\text{bola azul})\\[2ex]&=0,5+0,3\\[2ex]&=0,8\end{aligned}$

つまり、ボックスから青またはオレンジのボールを引き出す確率は 80% です。

非排他的イベントの追加ルールの例

イベントが排他的である場合の加算規則の具体例を見てきましたが、次に、イベントが排他的でない場合にこの法則がどのように使用されるかを見ていきます。

コインを 2 回投げた場合、少なくとも 1 回のトスで表になる確率はどれくらいですか?

この場合、最初のスローで「表」が得られ、2 番目のスローで「裏」が得られるため、イベントは相互に排他的ではありません。したがって、加算ルールの式は簡略化されず、次のようになります。

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

したがって、最初にラプラスの法則を適用して、コイントスで「表」が出る確率を計算する必要があります。

$P(\text{cara})=\cfrac{1}{2}=0,5$

さらに、2 つのイベントは独立しているため、次の積ルールを使用して 2 つのイベントの結合確率を計算できます。

$P(\text{cara}\cap \text{cara})=\cfrac{1}{2}\cdot \cfrac{1}{2}=0,5\cdot 0,5=0,25$

最後に、2 回のトスのうち少なくとも 1 回で表が出る確率を調べるには、加算ルールの式に値を代入して計算します。

$\begin{aligned}P(\text{cara}\cup \text{cara})&=P(\text{cara})+P(\text{cara})-P(\text{cara}\cap \text{cara})\\[2ex]&=0,5+0,5-0,25\\[2ex]&=0,75\end{aligned}$

結論として、コインを 2 回投げて少なくとも 1 回は表が出る確率は 75% です。

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る