原点を通した回帰: 定義と例

単純線形回帰は、1 つ以上の予測変数と応答変数の間の関係を定量化するために使用できる方法です。

単純な線形回帰モデルは次の形式になります。

y = β ₀ + β ₁ x

金：

• y : 応答変数の値
• β ₀ : x = 0 の場合の応答変数の値 (「切片」項と呼ばれます)
• β ₁ : x の 1 単位の増加に伴う応答変数の平均増加量
• x : 予測変数の値

このモデルの修正バージョンは原点回帰として知られており、x が 0 に等しい場合に y が 0 に等しくなります。

このタイプのモデルは次の形式になります。

y = _β1x

切片項がモデルから完全に削除されていることに注意してください。

このモデルは、予測変数がゼロの場合には応答変数もゼロでなければならないことが研究者によってわかっている場合に使用されることがあります。

現実の世界では、このタイプのモデルは林業や生態学の研究で最もよく使用されます。

たとえば、研究者は木の周囲を使用して木の高さを予測できます。指定された木の円周がゼロの場合、その木の高さはゼロでなければなりません。

したがって、回帰モデルをこのデータに当てはめる場合、元の項がゼロ以外であることは意味がありません。

次の例は、通常の単純な線形回帰モデルの近似と、原点を介して回帰を実装するモデルの違いを示しています。

例: 原点を通した回帰

生物学者が木の周囲を使用して回帰モデルを当てはめて木の高さを予測したいとします。彼女は外に出て、15 本の木のサンプルについて次の測定値を収集します。

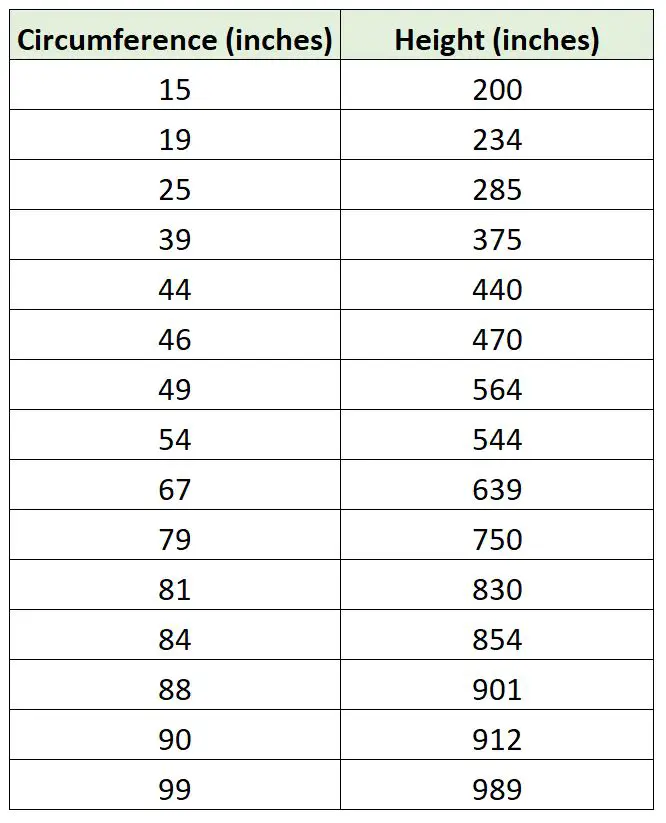
R で次のコードを使用すると、切片を使用しない回帰モデルで単純な線形回帰モデルを近似し、2 つの回帰直線をプロットできます。

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

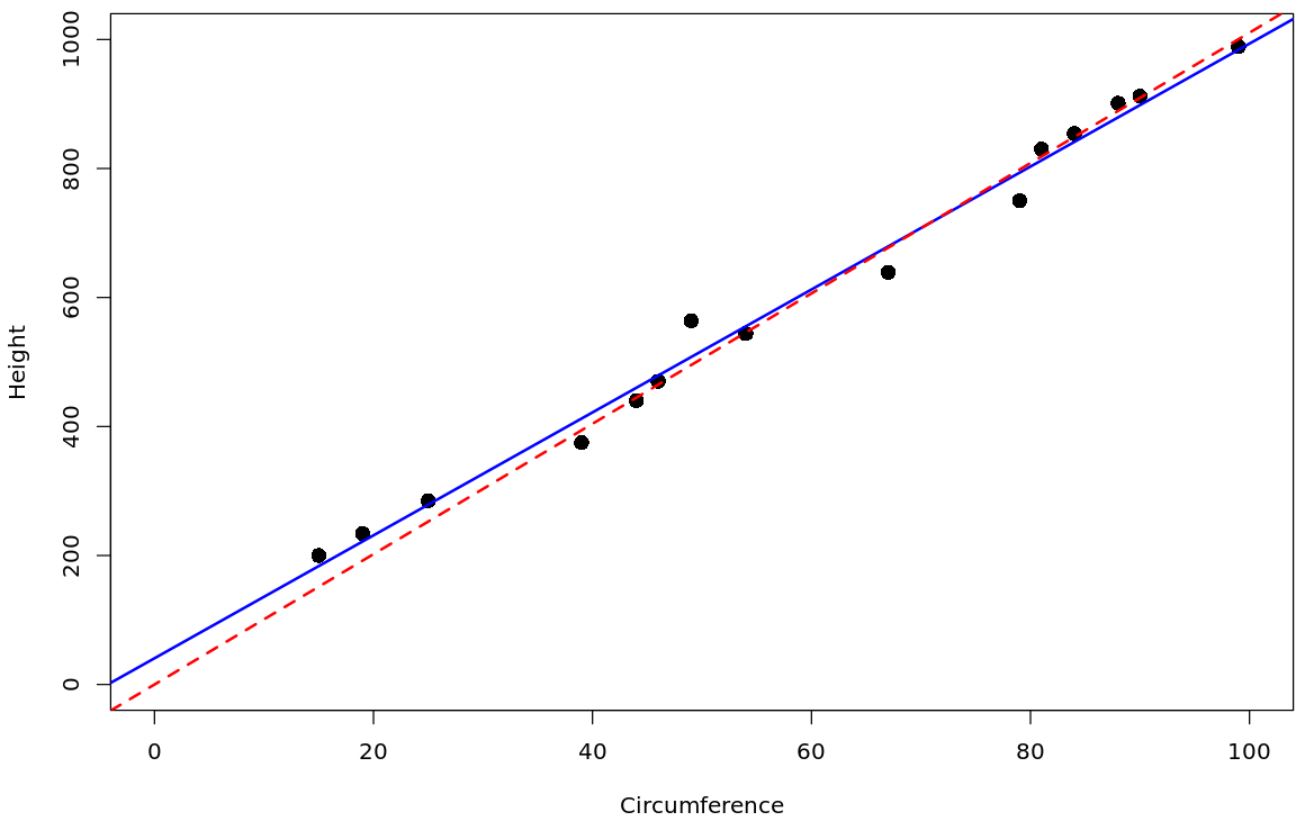
赤い点線は原点を通る回帰モデル、青い実線は通常の単純線形回帰モデルを表します。

R で次のコードを使用すると、各モデルの係数推定値を取得できます。

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

単純な線形回帰モデルの近似式は次のとおりです。

高さ = 40.6969 + 9.5296 (円周)

原点を介して回帰モデルに近似された方程式は次のとおりです。

高さ = 10.1057 (円周)

円周変数の係数推定値はわずかに異なることに注意してください。

原点経由回帰を使用する場合の注意事項

切片回帰を使用する前に、予測子変数の値 0 が応答変数の値 0 を意味することを絶対に確認する必要があります。多くのシナリオでは、確実に知ることはほぼ不可能です。

また、原点を推定する際の自由度を節約するために原点を介した回帰を使用する場合、サンプル サイズが十分に大きい場合には、実質的な違いが生じることはほとんどありません。

原点を介した回帰を使用することを選択した場合は、最終的な分析またはレポートで必ずその推論の概要を説明してください。

追加リソース

次のチュートリアルでは、線形回帰に関する追加情報を提供します。

単線形回帰の概要
重線形回帰の概要
回帰表の見方と解釈方法