多項分布の概要
多項分布は、各結果の発生確率が固定されている場合に、 k個の異なる結果に対して特定のカウント数を取得する確率を表します。
確率変数_は次の式で求められます。
確率 = n! * (p 1 x 1 * p 2 x 2 * … * p k x k ) / (x 1 ! * x 2 ! … * x k !)
金:
- n:イベントの総数
- x 1 :結果 1 が発生した回数
- p 1 :与えられた試行で結果 1 が発生する確率
たとえば、壺の中に赤いビー玉が 5 個、緑のビー玉が 3 個、青いビー玉が 2 個あるとします。壺からビー玉をランダムに 5 つ取り出し、交換すると、赤いビー玉が 2 つ、緑のビー玉が 2 つ、青いビー玉が 1 つ正確に得られる確率はいくらですか?
この質問に答えるには、次のパラメーターを使用して多項分布を使用できます。
- n :5
- x 1 (赤いビー玉の数) = 2、 x 2 (緑のビー玉の数) = 2、 x 3 (青いビー玉の数) = 1
- p 1 (赤色の確率) = 0.5、 p 2 (緑色の確率) = 0.3、 p 3 (青色の確率) = 0.2
これらの数値を式に代入すると、確率は次のようになります。
確率= 5! * (.5 2 * .3 2 * .2 1 ) / (2! * 2! * 1!) = 0.135 。
多項分布の練習問題
次の練習問題を使用して、多項分布の知識をテストしてください。
注:これらの質問に対する答えを計算するには、多項分布計算ツールを使用します。
問題 1
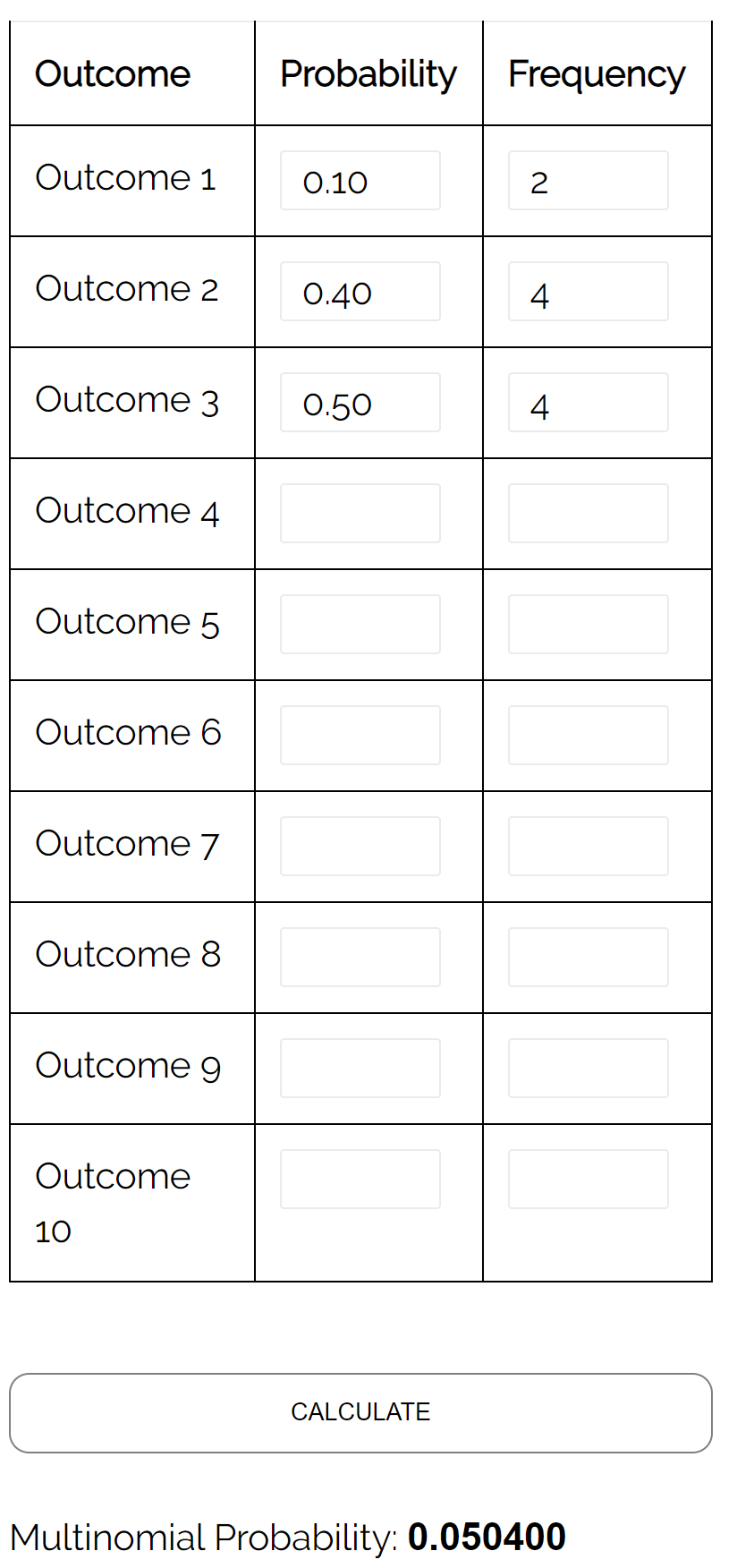
質問:市長選挙の 3 者投票では、候補者 A が票の 10%、候補者 B が票の 40%、候補者 C が票の 50% を獲得します。 10 人の有権者の無作為サンプルを選択した場合、2 人が候補 A に投票し、4 人が候補 B に投票し、4 人が候補 C に投票する確率はいくらですか?
回答:次の入力で多項分布計算ツールを使用すると、確率が0.0504 であることがわかります。
問題 2
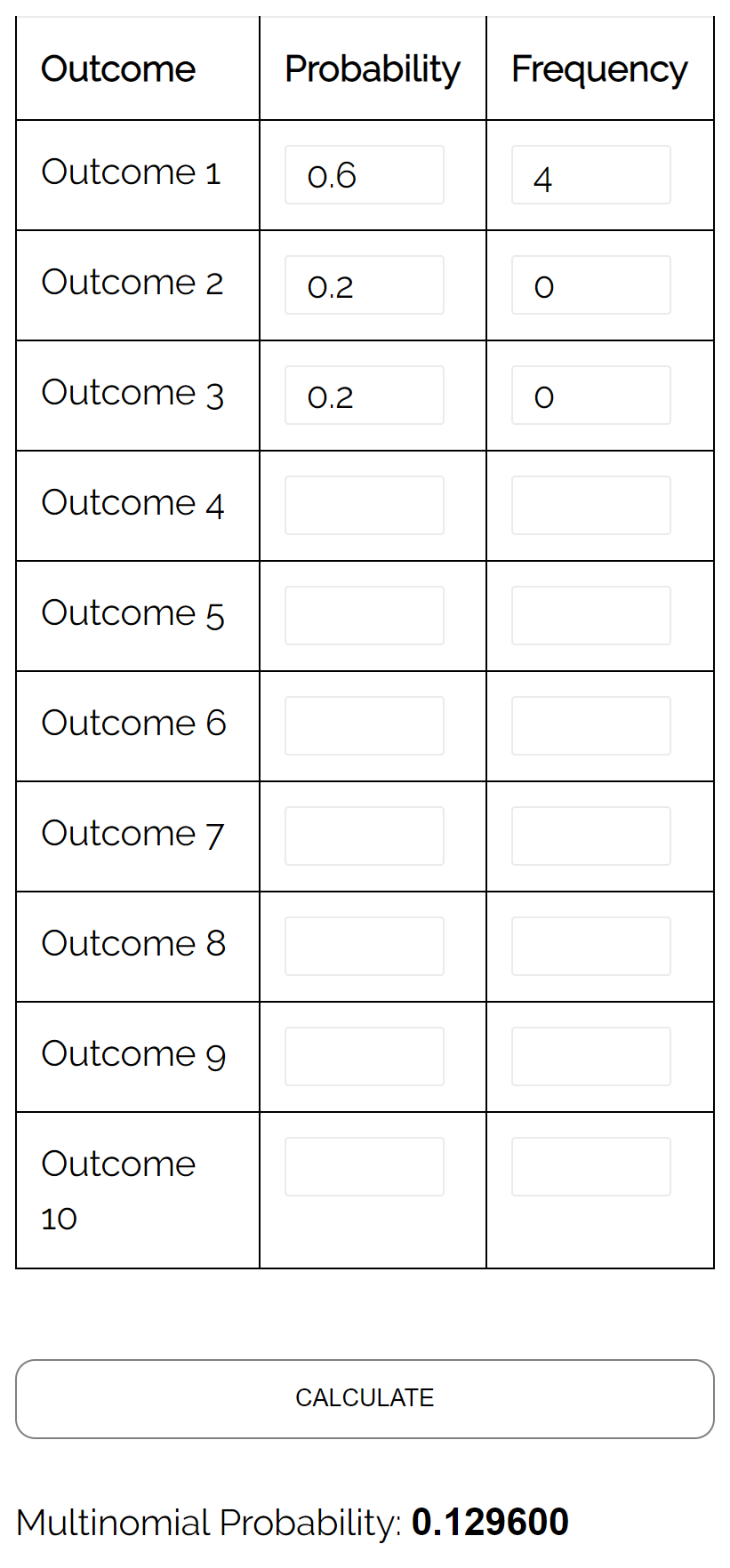
質問:骨壷に黄色のビー玉が 6 個、赤いビー玉が 2 個、ピンクのビー玉が 2 個入っているとします。代替品を使用して壺から 4 つのボールをランダムに選択した場合、4 つのボールすべてが黄色である確率はどれくらいですか?
回答:次の入力で多項分布計算ツールを使用すると、確率が0.1296 であることがわかります。
問題 3
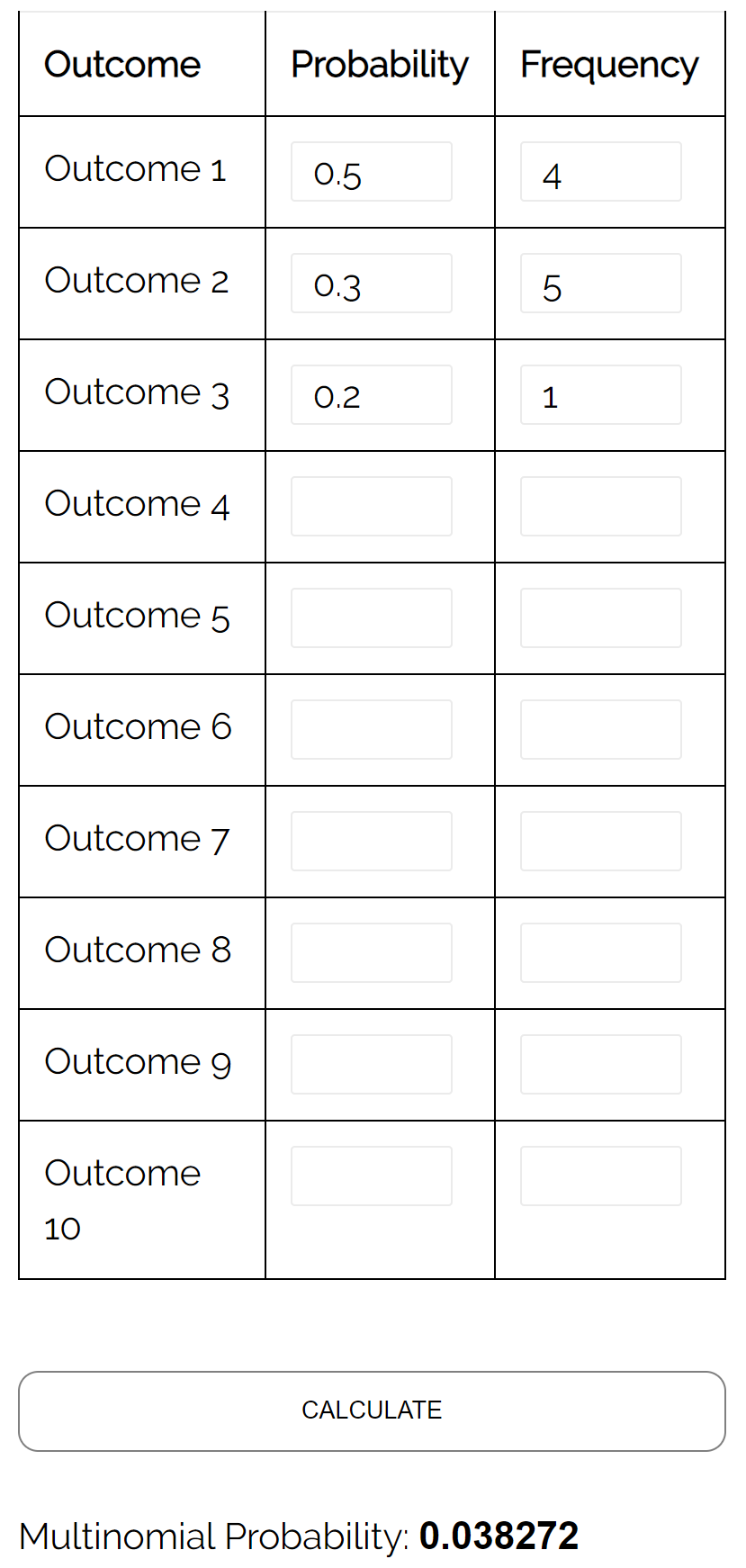
質問: 2 人の学生がチェスを対戦しているとします。生徒 A が特定のゲームに勝つ確率は 0.5、生徒 B が特定のゲームに勝つ確率は 0.3、特定のゲームで引き分けになる確率は 0、2 です。彼らが 10 ゲームをプレイする場合、プレーヤー A が 4 回勝ち、プレーヤー B が 5 回勝ち、彼らが 1 回引き分けになる確率は?
回答:次の入力で多項分布計算ツールを使用すると、確率が0.038272 であることがわかります。
追加リソース
次のチュートリアルでは、統計における他の一般的な分布について説明します。