大数の法則: 定義と例
大数の法則は、サンプルのサイズが大きくなるにつれて、 サンプルの平均値が期待値に近づくことを示しています。
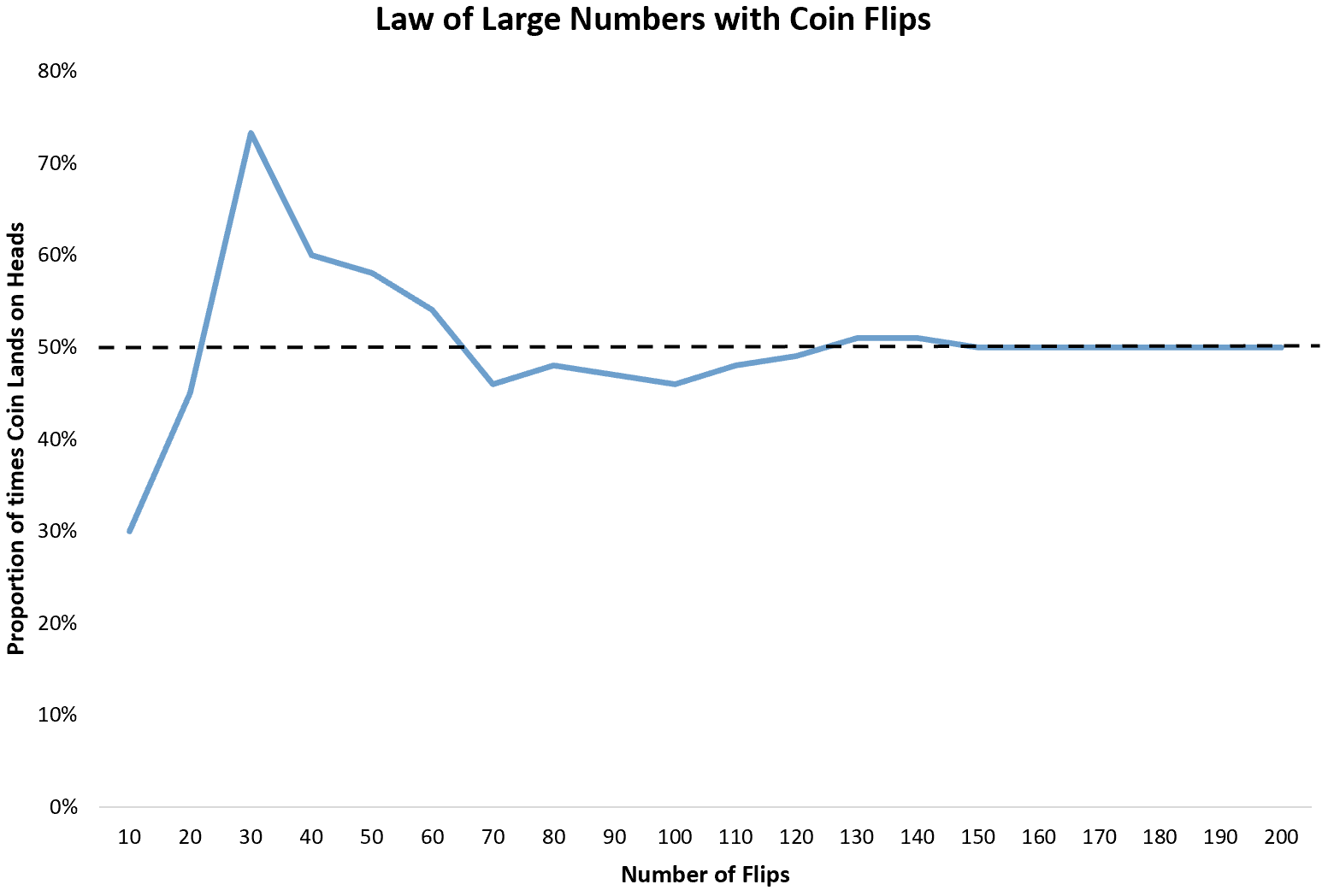
最も基本的な例はコイン投げです。コインを投げるたびに、表が出る確率は 1/2 です。したがって、無限回のトスで表が現れると予想される割合は 1/2 または0.5です。
ただし、コインを 10 回投げると、表が出るのは 3 回だけであることがわかります。 10 回のフリップはサンプル サイズが小さいため、ヘッドの割合が0.5に近くなるという保証はありません。
さらに 10 回コインを投げ続けると、20 回中 9 回表が出ることがわかります。さらに 10 回投げると、30 回中 22 回表が出ることがわかります。
コインを投げると、表が出る回数の割合は、予想される割合0.5に収束します。
この大数の法則の単純な考え方は、現実のさまざまな種類のビジネスや業界に適用されています。
カジノにおける大数の法則
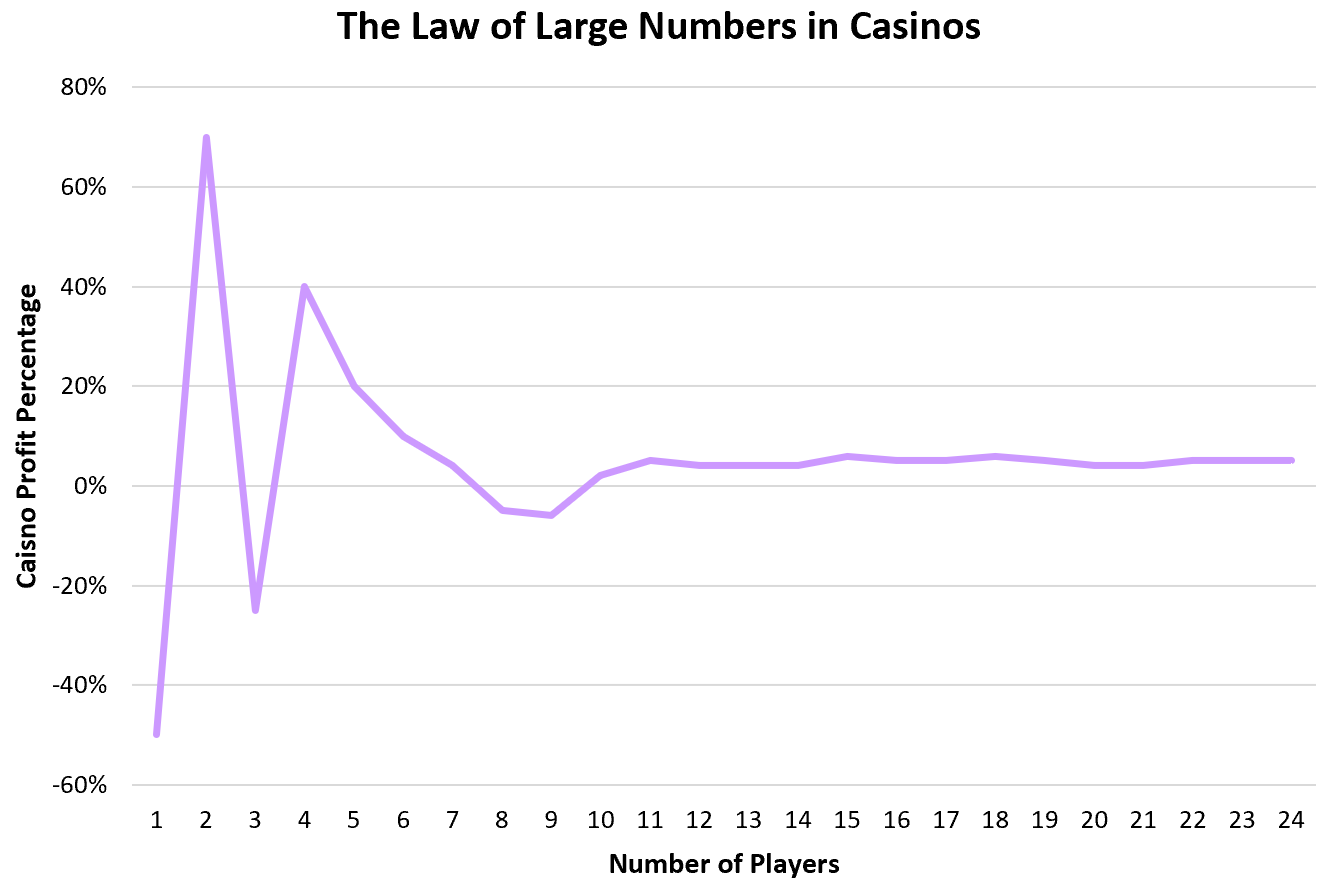
カジノは大数の法則に基づいて確実に利益を生み出します。ほとんどのゲームでは、カジノは約 51 ~ 55% の確率で勝ちます。これは、個人が幸運に恵まれて多額の賞金を獲得することもありますが、数万人の個人プレーヤーのうち、カジノは予想される 51 ~ 55% の確率で勝つことを意味します。
たとえば、ジェシカはカジノでいくつかのゲームをプレイして、50 ドルを獲得できます。
マイクは数試合をプレイして 70 ドルを失う可能性もあります。
ジョンはいくつかのゲームをプレイして 25 ドルを獲得できるでしょう。
スーザンは数ゲームをプレイすると 40 ドルを失う可能性があります。
お金を獲得するプレイヤーもいれば、お金を失うプレイヤーもいますが、ゲームの設計方法により、カジノは何千人ものプレイヤーの中から確実に勝つことができます。
保険における大数の法則
保険会社も利益を維持するために大数の法則に依存しています。
基本的な考え方は、何千もの保険会社が毎月一定の保険料を支払う人々に保険を提供することができ、保険に加入している人々のうち実際に予期せぬ大きな出費を支払うために保険を利用する必要があるのはごく一部の人だけである、というものです。
たとえば、1,000 人がそれぞれ年間 1,000 ドルの保険料を支払うと、保険会社には 1,000,000 ドルの利益が生まれます。
ただし、90 人がさまざまな事故に関連する予期せぬ出費をカバーするために保険会社からそれぞれ 10,000 ドルを受け取る必要があり、その結果、保険会社は 900,000 ドルの損失を被ることになります。
最終的に、保険会社は 1,000,000 ドル – 900,000 ドル = 100,000 ドルの利益を上げます。
これは、保険会社が平均して何千人もの人々に対してかなり予測可能な利益を期待できることを意味します。
この経済モデルが機能するのは、保険会社が多数の人々に保険を掛けているからです。 10 人だけを保険に加入した場合、予期せぬ多額の出費で事業が壊滅する可能性があるため、リスクが高すぎます。
したがって、保険会社は大数の法則に基づいて、予測可能な方法で利益を予測します。
再生可能エネルギーにおける大数の法則
大数の法則は再生可能エネルギー企業でも利用されています。
基本的な考え方は、風力タービンとソーラー パネルが発電機に電力を供給し、ビジネスのさまざまな部分で電力を生成できるというものです。ただし、屋外には風も太陽もありません。つまり、風力タービンやソーラー パネルが常に発電機用に信頼性の高い電力を生成できるとは限りません。
再生可能エネルギー企業がこの問題を回避する方法は、何万もの風力タービンやソーラーパネルを単一の送電網に接続し、これらのエネルギー源が信頼できる量のエネルギーを生産できる可能性を大幅に高めることです。ネットワークにエネルギーを供給します。
また、エンジニアは数万台の風力タービンやソーラー パネルの予想平均値を単純に算出できるため、これらの電源によって生成されるエネルギーの量を予測するのもはるかに簡単になります。
この現象の詳細な説明は、Scientific American の記事に記載されています。