学生の t 分布
この記事では、Student t 分布とは何か、またその用途について説明します。さらに、スチューデントの t 分布のグラフと、このタイプの確率分布の特徴が示されています。
学生の分布とは何ですか?
スチューデントの t 分布は、統計で広く使用されている確率分布です。具体的には、スチューデントの t 分布はスチューデントの t 検定で使用され、2 つのサンプルの平均間の差を決定し、信頼区間を確立します。
スチューデントの t 分布は、統計学者ウィリアム シーリー ゴセットによって 1908 年に「スチューデント」という仮名で開発されました。
スチューデントの t 分布は、観測値の総数から 1 単位を減算することで得られる自由度の数によって定義されます。したがって、スチューデントの t 分布の自由度を決定する式はν=n-1です。
![Rendered by QuickLaTeX.com \begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png)
スチューデントの t 分布グラフ
スチューデントの t 分布の定義がわかったので、そのグラフがどのようなものかを見てみましょう。したがって、以下では、さまざまな自由度を持つスチューデントの t 分布のいくつかの例をグラフで見ることができます。
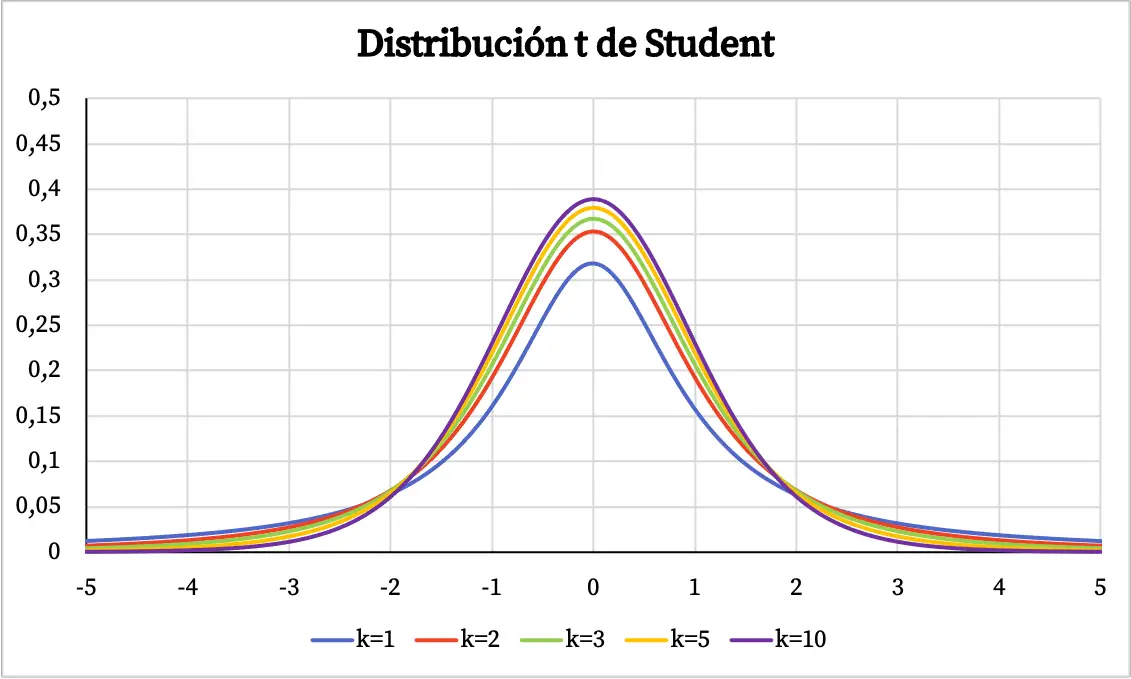
スチューデントの t 分布のグラフから、次の特性を推定できます。
- スチューデント t 分布は 0 を中心として対称であり、釣鐘型になります。
- スチューデントの t 分布は正規分布よりも分散しています。つまり、スチューデントの t 分布の曲線は幅が広くなります。
- スチューデントの t 分布の自由度が大きくなるほど、その分散は低くなります。
上のグラフでは、スチューデントの t 分布の密度関数が自由度に対してプロットされています。ただし、スチューデントの t 分布の累積確率関数がどのように変化するかを以下で確認できます。
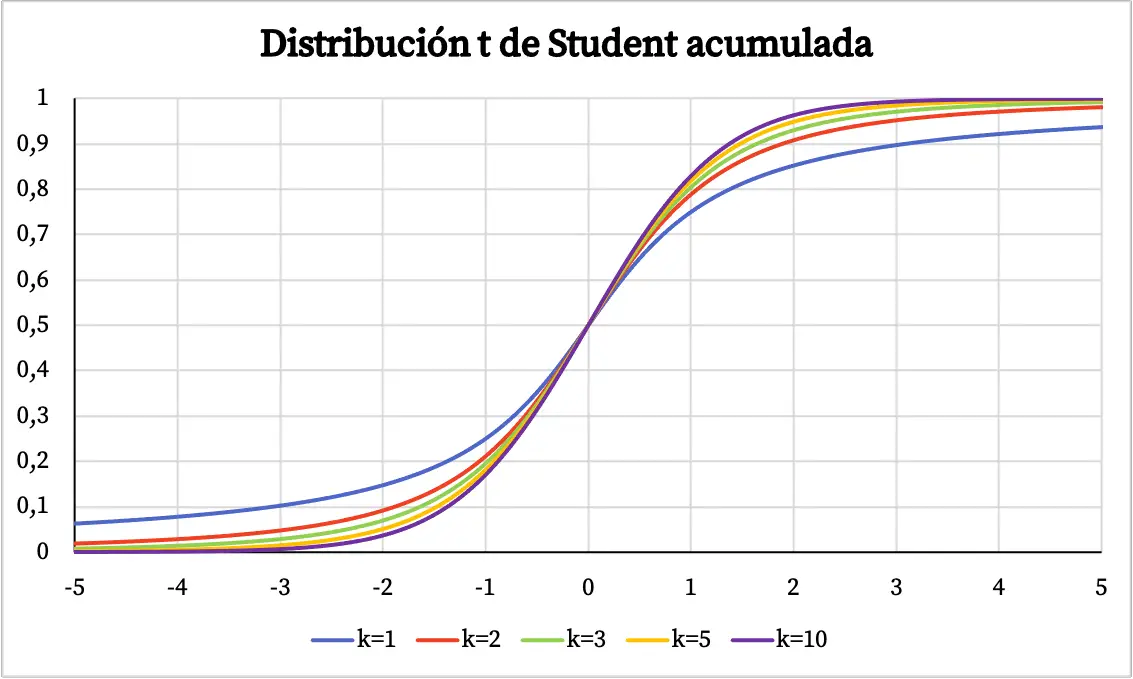
スチューデントの t 分布の特徴
スチューデントの t 分布の最も重要な特徴を以下に示します。
- Student t 分布の領域は実数で構成されます。
![]()
- 複数の自由度を持つスチューデントの t 分布の場合、分布の平均は 0 に等しくなります。
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>スチューデントの t 分布の分散は、次の式を使用して計算できます。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>スチューデントの t 分布の中央値と最頻値は、自由度の数に関係なく、常に 0 です。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png)
- スチューデント t 分布の密度関数は、次の式で定義されます。
![]()
- スチューデントの t 分布の累積確率分布関数は、次の式で定義されます。
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png)
- 自由度が 3 より大きいスチューデント t 分布の場合、対称分布であるため、非対称係数は 0 になります。
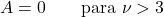
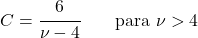 スチューデントの t 分布の応用
スチューデントの t 分布の応用
スチューデントの t 分布は、統計で広く使用されている確率分布です。実際、仮説と信頼区間を検定するために使用される Student の t 検定さえあります。
したがって、スチューデントの t 分布を使用すると、2 つのサンプルの平均値の差を分析できます。より正確には、2 つのサンプルの平均値が大きく異なるかどうかを判断するために使用されます。同様に、スチューデントの t 検定は、線形回帰分析から得られた直線に傾きがあるかどうかを確認するために使用されます。
つまり、スチューデントの t 分布の適用は、理論的には正規分布に従うデータセットの分析に依存しますが、このタイプの分布を使用するには観測値の総数が少なすぎます。