学生の t 検定
この記事では、Student t 検定とは何なのか、また統計で何に使用されるのかについて説明します。したがって、スチューデントの t 検定がどのように実行されるか、スチューデントの t 検定のさまざまな種類とそれぞれの公式がわかります。
スチューデントの t 検定とは何ですか?
Student の t 検定は、 T 検定または単にt 検定とも呼ばれ、検定統計量がStudent の t 分布に従う統計検定です。したがって、統計学では、仮説検定の帰無仮説を棄却または受け入れるために、スチューデントの t 検定が使用されます。
具体的には、スチューデントの t 検定は、研究対象の母集団が正規分布に従う仮説検定に使用されますが、サンプル サイズが小さすぎて母集団の分散を知ることができません。
つまり、スチューデントの t 検定は、特定の仮説検定の研究仮説を拒否または受け入れるために使用されます。たとえば、スチューデントの t 検定は、1 つのサンプル、独立したサンプル、または関連するサンプルの仮説を検定するために使用されます。次に、それぞれのケースで Student の t 検定がどのように計算されるかを見ていきます。
スチューデントの t 検定の種類
スチューデントの t 検定には 3 つのタイプがあります。
- 1 サンプル スチューデントの t 検定– サンプル平均値に関する仮説を検定するために使用されます。
- 2 つの独立したサンプルに対するスチューデントの t 検定: 2 つの独立したサンプルの平均間の差に関する仮説を検定できます。
- 2 つのペアのサンプル (または関連するサンプル) に対するスチューデントの t 検定– 2 回テストされたサンプルの平均に関する仮説を調査するために使用されます。
Student の t 検定のサンプル
標本平均の仮説検定は、検定の帰無仮説と対立仮説が母集団の平均値について何かを言うものです。
1 サンプル Student t 検定の式は次のとおりです。

金:
-

は平均の仮説検定統計量であり、スチューデントの t 分布によって定義されます。
-

はサンプル平均です。
-

仮説検定で提案された平均値です。
-

は標本標準偏差です。
-

はサンプルサイズです。
スチューデントの t 検定の値が計算されたら、臨界値を含む統計検定の結果を解釈して、帰無仮説を棄却するかどうかを判断する必要があります。
- 平均の仮説検定が両側である場合、スチューデントの t 検定の絶対値が臨界値 t α/2|n-1より大きい場合、帰無仮説は棄却されます。
- 平均の仮説検定が右裾に一致する場合、スチューデントの t 検定値が臨界値 t α|n-1より大きい場合、帰無仮説は棄却されます。
- 平均の仮説検定が左裾に一致する場合、スチューデントの t 検定値が臨界値 -t α|n-1より小さい場合、帰無仮説は棄却されます。
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
重要なテスト値は生徒の分布表から取得されることに注意してください。
独立したサンプルに対するスチューデントの t 検定
独立したサンプルに対するスチューデントの t 検定は、2 つの母集団の平均値間の関係の仮説、たとえば、2 つの母集団の平均値が異なる、または母集団 A の平均が母集団 A の平均よりも大きいという仮説を棄却または受け入れるために使用されます。 。人口B。
ただし、この場合、スチューデントの t 検定の式は、母集団の分散が等しいと仮定できるかどうかによって異なります。次に、考えられる 2 つのケースを見ていきます。
未知の等しい偏差
母集団分散が不明であるが等しいと仮定される場合、独立サンプルのスチューデント t 検定を計算する式は次のとおりです。

金:
-

は、未知の分散を伴う平均の差の仮説検定統計量であり、自由度 n 1 + n 2 -2 のスチューデントの t 分布に従います。
-

は母集団 1 の平均です。
-

は母集団 2 の平均です。
-

はサンプル 1 の平均です。
-

はサンプル 2 の平均です。
-

プールされた標準偏差です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。
2 つのサンプルの標準偏差を組み合わせた値は、次の式を使用して計算されます。

未知のさまざまなバリエーション
母集団の分散が不明で、さらに異なると仮定される場合、独立サンプルのスチューデントの t 検定を計算する式は次のとおりです。

金:
-

は、未知の分散を伴う平均の差の仮説検定統計量であり、スチューデントの t 分布に従います。
-

は母集団 1 の平均です。
-

は母集団 2 の平均です。
-

はサンプル 1 の平均です。
-

はサンプル 2 の平均です。
-

は母集団 1 の標準偏差です。
-

は母集団 2 の標準偏差です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。
ただし、この場合、スチューデントの t 分布の自由度は次の式を使用して計算されます。

対応のあるサンプルまたは関連サンプルに対するスチューデントの t 検定
このテストは、研究対象の 2 つのサンプルが相互に関連している場合に使用され、実際には 2 回 (毎回異なる条件で) 分析された個人の 1 つのサンプルになります。
たとえば、数学と統計コースの生徒の成績を分析して、2 つの科目の平均値に大きな差があるかどうかを確認できます。この場合、各生徒の数学の成績は、同じ生徒の統計の成績にリンクされます。
対応のあるサンプルまたは関連サンプルに対するスチューデントの t 検定の公式は次のとおりです。
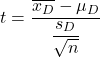
金:
-

は、一対の平均に対する仮説検定統計量であり、スチューデントの t 分布によって定義されます。
-
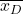
データの差によって形成されるサンプルの平均です。
-
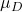
仮説検定で提案された平均値です。
-
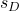
は、データの差によって形成されるサンプルの標準偏差です。
-

はサンプルサイズです。
スチューデントの t 検定の仮定
Student の t 検定を実行するには、次の条件を満たす必要があります。
- 連続性– サンプル データは連続的です。
- ランダム性: データサンプルはランダムに選択されました。
- Homogeneity : データサンプルの分散は均一です。
- 正規性– データ サンプルを定義する分布はほぼ正規です。
スチューデントの t 検定の実行方法
最後に、要約として、Student の t 検定を実行するために従うべき手順を詳しく説明します。