Excel で対応のあるサンプルの t 検定を実行する方法
対のあるサンプルの t 検定は、一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つのサンプルの平均を比較するために使用されます。
このチュートリアルでは、Excel で対応のあるサンプルの t 検定を実行する方法について説明します。
Excel で対応のあるサンプルの t 検定を実行する方法
特定のカリキュラムが特定の試験における生徒の成績に大きな影響を与えるかどうかを知りたいとします。これをテストするために、クラスの 20 人の生徒に事前テストを受けてもらいます。その後、各生徒に 2 週間のカリキュラムに参加してもらいます。その後、学生は同様の難易度のテストを再受験します。
1 回目と 2 回目のテストの平均スコアの差を比較するには、各生徒の最初のテストのスコアが 2 回目のテストのスコアと関連付けられる可能性があるため、対応のあるサンプルの t 検定を使用します。
次の画像は、各生徒のテスト前スコアとテスト後スコアを示しています。
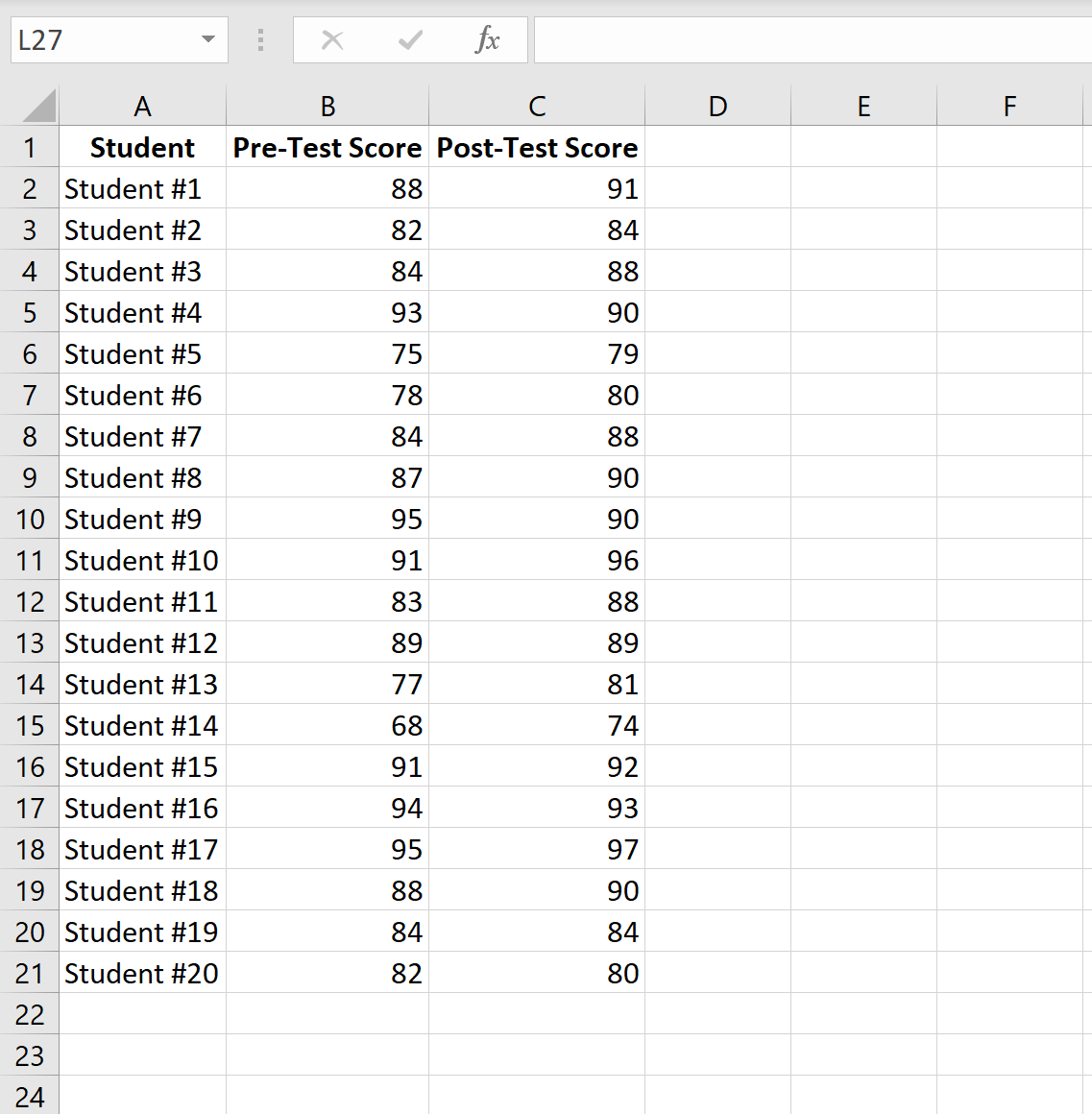
次の手順を実行して、対応のあるサンプルの t 検定を実行し、テスト前とテスト後の平均テスト スコアに有意な差があるかどうかを判断します。
ステップ 1: データ分析ツールを開きます。
上部リボンの「データ」タブで「データ分析」をクリックします。
クリックするこのオプションが表示されない場合は、まず完全に無料のAnalysis ToolPak をダウンロードする必要があります。
ステップ 2: 使用する適切なテストを選択します。
[T 検定: 平均に対する対応のある 2 つのサンプル]オプションを選択し、[OK] をクリックします。
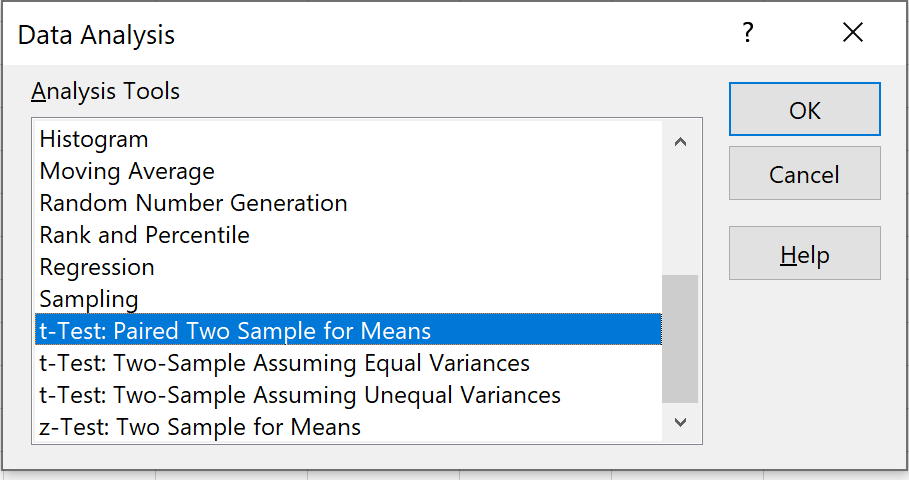
ステップ3：必要な情報を入力します。
変数 1 (テスト前のスコア)、変数 2 (テスト後のスコア)、仮説の平均差の値の範囲を入力します (この場合、真の差があるかどうかを知りたいため、「0」を入力します)テスト前とテスト後のスコアの平均は 0)、テスト結果を表示する出力範囲。次に「OK」をクリックします。
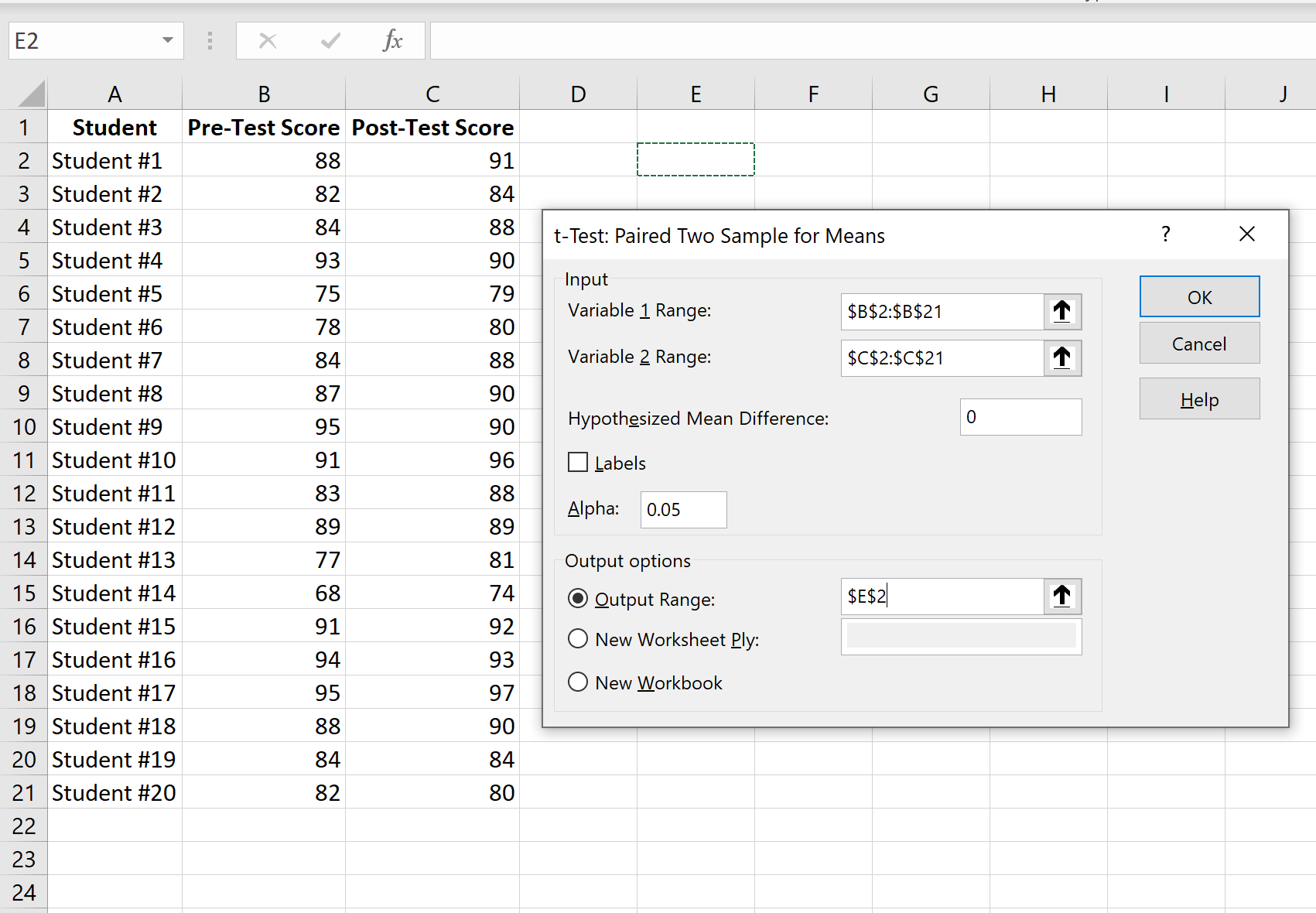
ステップ 4: 結果を解釈します。
前の手順で [OK] をクリックすると、t 検定の結果が表示されます。
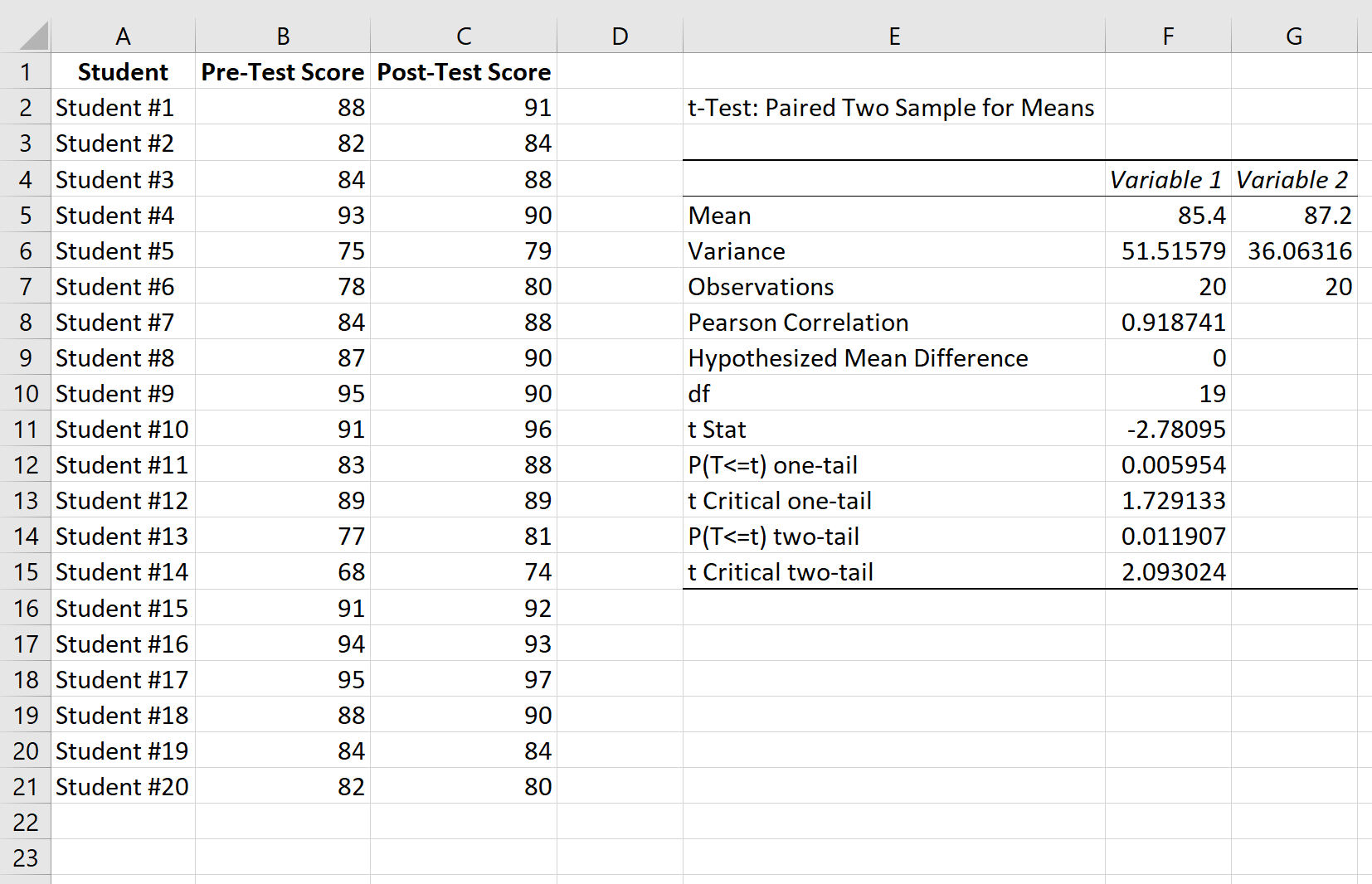
結果を解釈する方法は次のとおりです。
平均:これは各サンプルの平均です。テスト前の平均スコアは85.4 、テスト後の平均スコアは87.2です。
分散:これは各サンプルの分散です。テスト前のスコアの分散は51.51 、テスト後のスコアの分散は36.06です。
観測値:これは、各サンプル内の観測値の数です。どちらのサンプルにも20 個の観測値が含まれています。
ピアソン相関:テスト前のスコアとテスト後のスコアの間の相関関係。 0.918であることがわかります。
仮説の平均差: 「仮説」についての数値は、2 つの平均の差です。この場合、テスト前とテスト後のスコアに差があるかどうかをテストしたいため、 0を選択しました。
df: t 検定の自由度。これは、n-1 として計算されます (n はペアの数です)。この場合、 df = 20 – 1 = 19となります。
t Stat: t検定統計量。 -2.78と判明します。
両側 P(T<=t):両側 t 検定の p 値。この場合、 p = 0.011907 です。これは alpha = 0.05 より小さいため、帰無仮説を棄却します。テスト前とテスト後の平均スコアの間に統計的に有意な差があると言える十分な証拠があります。
t 両側臨界値:これは、 α = 0.05 および df = 19 の両側検定に対応する t 分布表内の値を特定することによって求められる検定の臨界値です。これは2 であることがわかります。 093024 。 t検定統計量の絶対値がこの値より大きいため、帰無仮説を棄却します。テスト前とテスト後の平均スコアの間に統計的に有意な差があると言える十分な証拠があります。
p 値アプローチと臨界値アプローチはどちらも同じ結論に至ることに注意してください。
追加リソース
次のチュートリアルでは、Excel で他の t 検定を実行する方法を説明します。
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る