対応のある t 検定と対応のない t 検定: 違いは何ですか?
統計学では、2 つのタイプの2 サンプル t 検定があります。
対応のある t 検定: 1 つのサンプルの各個人が他のサンプルにも出現する場合に、2 つのサンプルの平均を比較するために使用されます。
対応のない t 検定: 1 つのサンプルの各個人が他のサンプルの各個人から独立している場合に、2 つのサンプルの平均を比較するために使用されます。
注:対応のない t 検定は、一般的に独立サンプル t 検定と呼ばれます。
たとえば、教授が 2 つの異なる学習手法が試験の平均点の違いにつながるかどうかを判断したいとします。
対応のある t 検定を実行するには、10 人の学生を募集し、1 つの学習テクニックを 1 か月間使用して試験を受けさせ、次に 2 番目の学習テクニックを 1 か月間使用して同じ難易度の別の試験を受けてもらいます。
データは次のようになります。
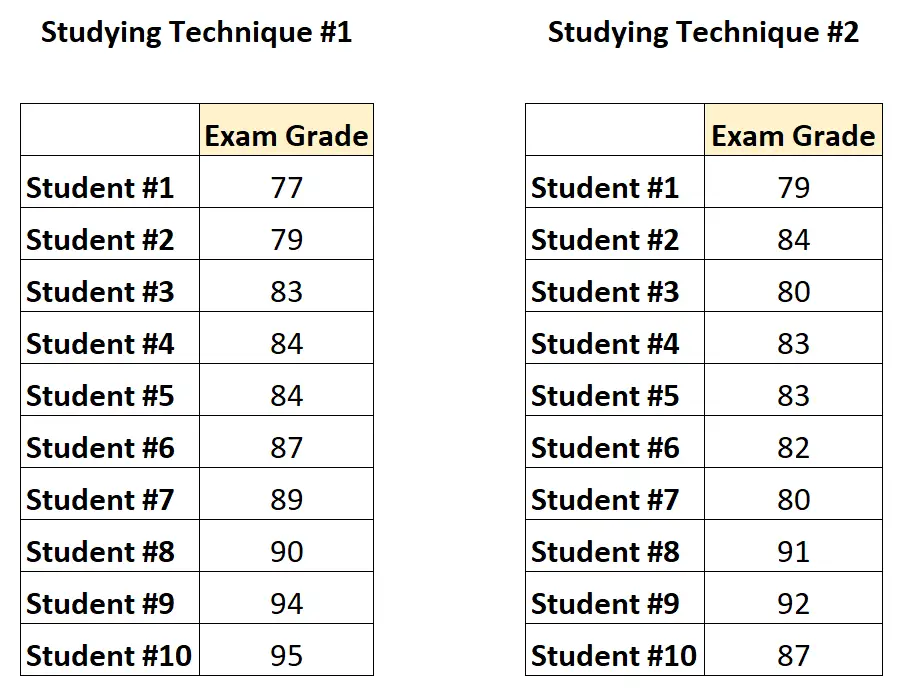
各学生は各グループに所属するため、教授は対応のある t 検定を実行して、2 つのグループ間で平均スコアが異なるかどうかを判断します。
対応のない t 検定を実行するには、合計 20 人の学生を募集し、ランダムに 10 人ずつ 2 つのグループに分けることができます。一方のグループには 1 か月間ある学習テクニックを使用するように依頼し、もう一方のグループには「2 番目の学習テクニックを 1 か月間使用する」ように依頼することができます。月。月にすべての生徒に同じ試験を受けさせます。
データは次のようになります。
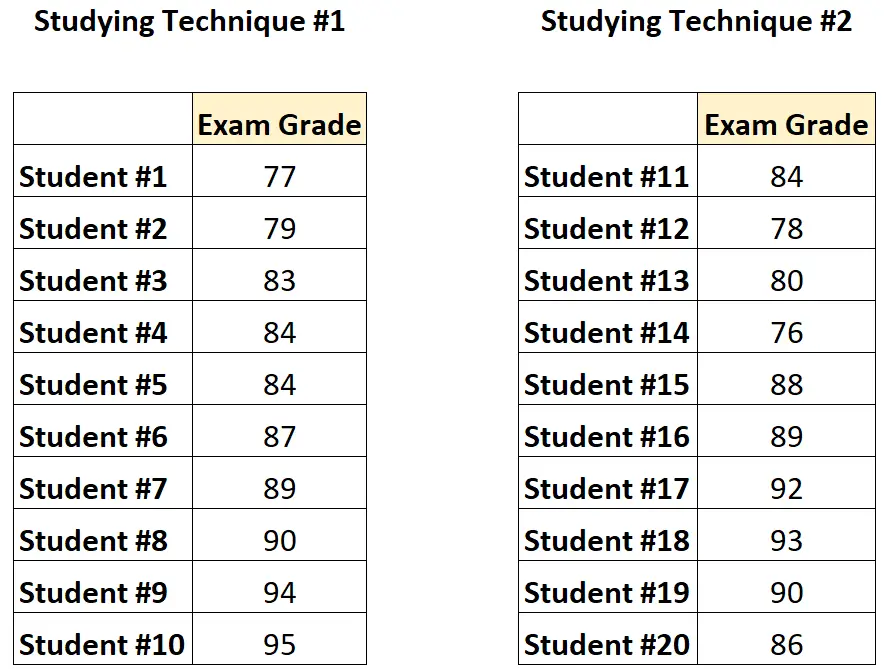
一方のグループの学生はもう一方のグループの学生から完全に独立しているため、教授は対応のない t 検定を実行して、2 つのグループの平均スコアが異なるかどうかを判断します。
仮説
対応のある t 検定と対応のない t 検定の両方で、次の仮定が行われます。
- 両方のサンプルからのデータは、 ランダム サンプリング方法を使用して取得されました。
- 両方のサンプルのデータはほぼ正規分布するはずです。
- どちらのサンプルにも極端な外れ値があってはなりません。
テスト結果の信頼性を確保するには、t 検定を実行する前にこれらの仮定を検証する必要があります。
長所と短所
対応のある t 検定には次の利点があります。
- より少ないサンプルが必要です。前の例の対応のある t 検定では合計 10 人の生徒のみが必要でしたが、対応のない t 検定では合計 20 人の生徒が必要であることに注意してください。
- 各サンプルには、同じ特性を持つ個体が含まれています。どちらのグループにも、能力や知性などを備えた個人がいることが保証されています。同じ個人が各グループに現れるため、等しいです。
ただし、対応のある t 検定には次のような潜在的な欠点があります。
- サンプルサイズを削減できる可能性。個人が研究から脱落した場合、その個人が各グループに含まれるため、各グループのサンプル サイズは 1 つ減ります。
- 順序効果の可能性。順序効果とは、個人に治療が提供された順序による 2 つのグループ間の結果の違いを指します。たとえば、ある人は、勉強技術のせいではなく、単に受験スキルが向上したという理由だけで、2 回目の試験の成績が向上する可能性があります。
対応のある t 検定と対応のない t 検定のどちらを使用するかを決定するときは、これらの長所と短所を念頭に置いてください。
追加リソース
対応のある t 検定をより深く理解するには、次のチュートリアルを確認してください。
また、対応のない t 検定 (独立サンプル t 検定とも呼ばれます) をよりよく理解するには、次のチュートリアルを使用してください。