グラフで対数スケールを使用する必要があるのはどのような場合ですか?

グラフを作成するときに対数スケールを使用することが合理的な一般的なシナリオが 2 つあります。

シナリオ 1:いくつかの値が他のすべての値よりも大幅に高くなります。

• 対数スケールを使用すると、グラフ上の小さい値を視覚化しやすくなります。

シナリオ 2:生の変化ではなく、変化率を分析したいとします。

• 対数スケールを使用すると、時間の経過に伴う値の変化の割合を視覚化しやすくなります。

次の例は、各シナリオが現実世界でいつ発生する可能性があるかを示しています。

シナリオ 1: いくつかの値が他の値よりもはるかに大きい場合に対数スケールを使用する

10 社の異なる企業の年間収益を視覚化し、そのうちの 2 社が他のすべての企業よりも大幅に収益が高いとします。

収益を線形スケールで見た場合のヒストグラムは次のようになります。

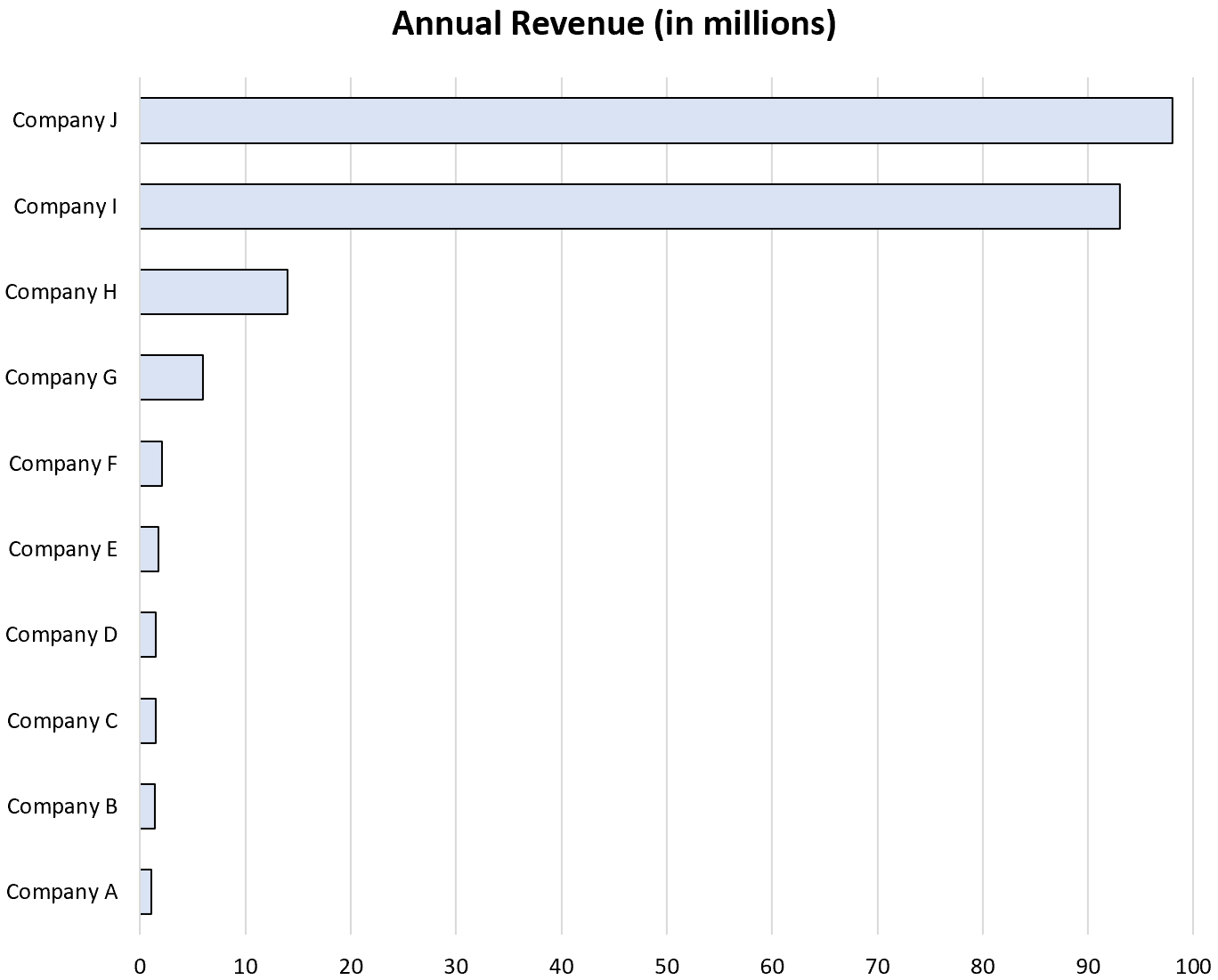
グラフ上の最小値を読み取り、最小値間の差異を確認することは非常に困難であることに注意してください。

同じ棒グラフを対数スケールで表示すると次のようになります。

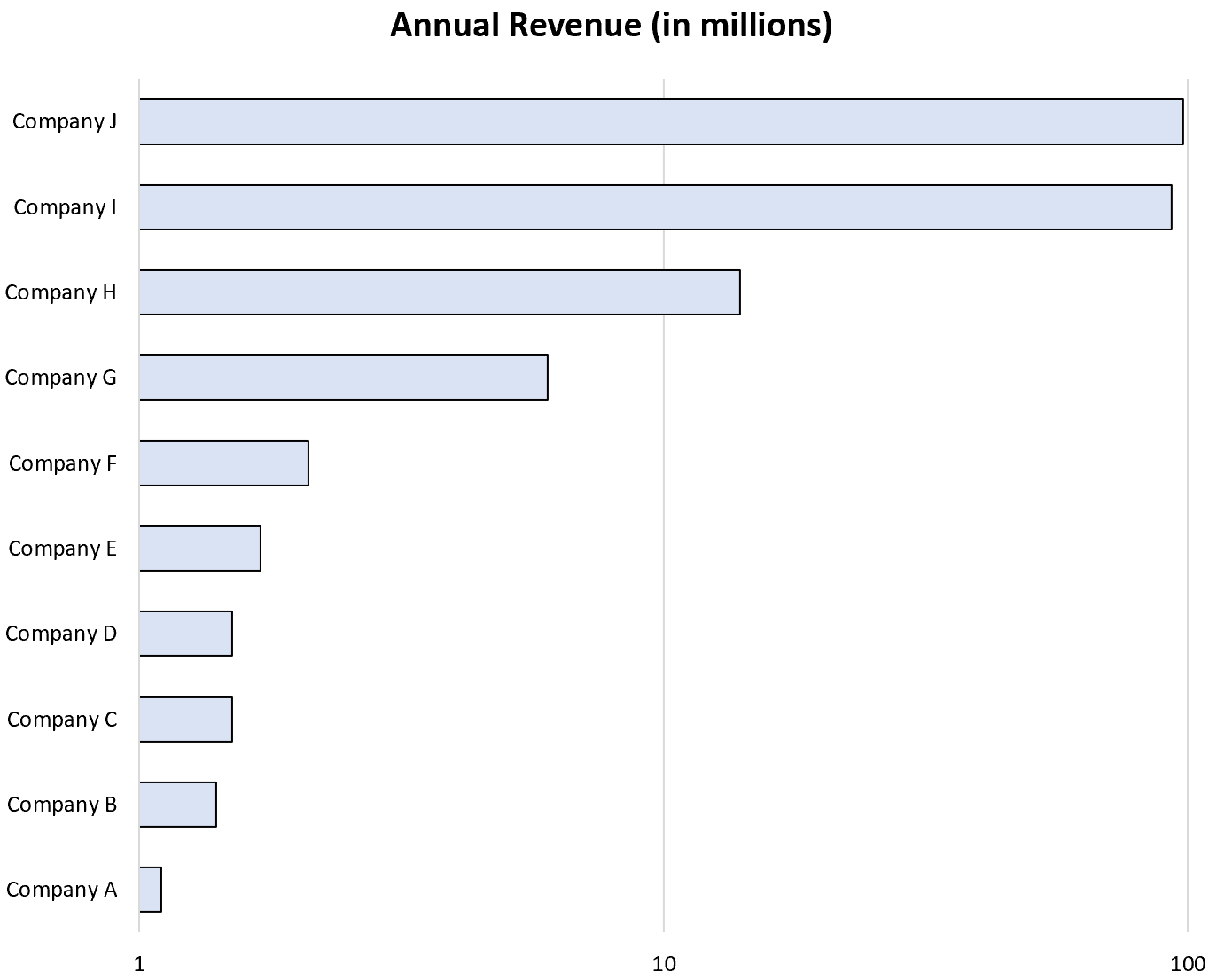
線形スケールよりも対数スケールを使用した方が、小さい値を区別するのがいかに簡単であるかに注目してください。

シナリオ 2: 対数スケールを使用して変化率を視覚化する

年間 6% 成長する株式に 10 万ドルを投資したとします。

30 年間の投資を線形スケールで表す折れ線グラフは次のとおりです。

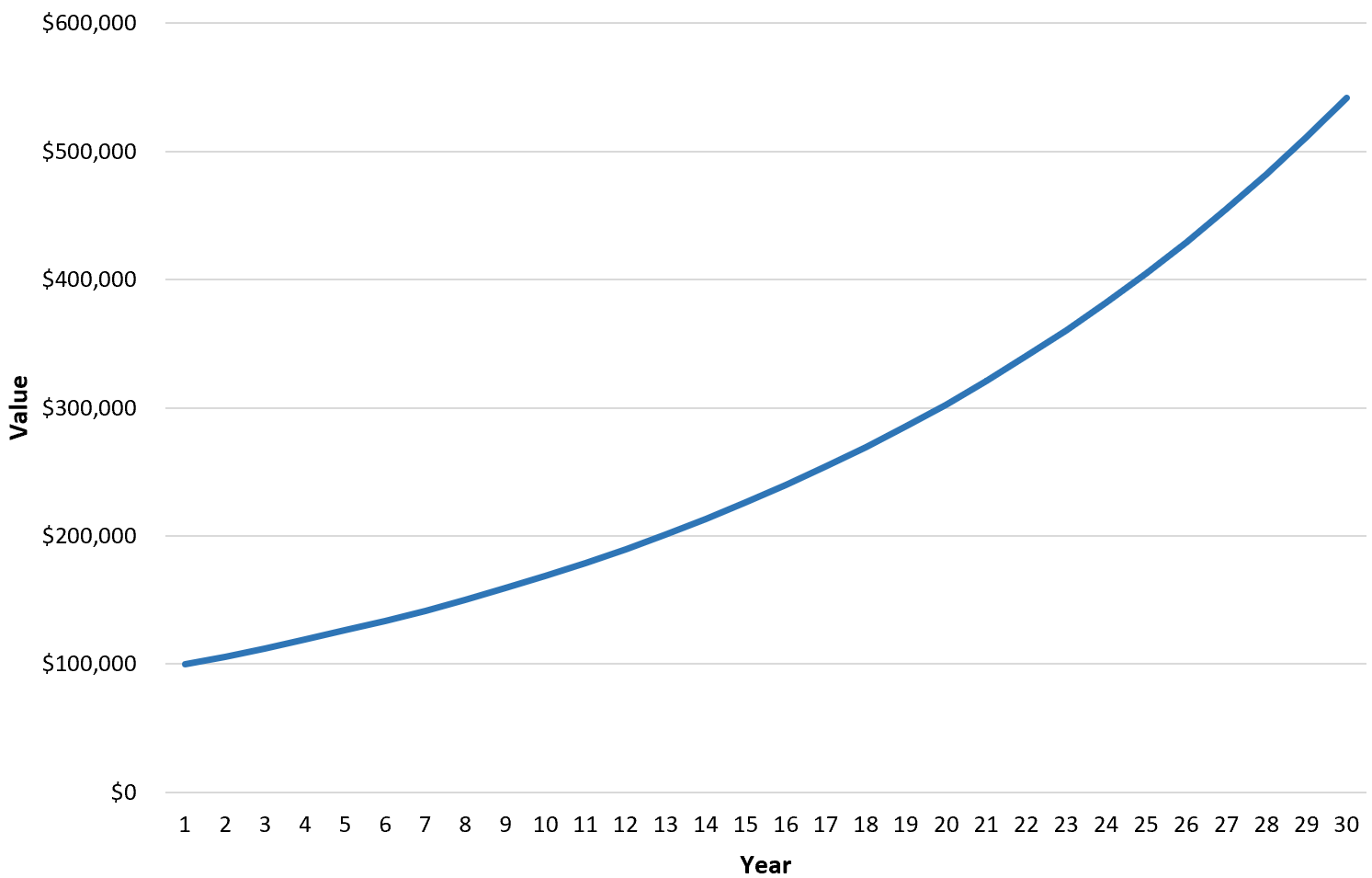
このグラフは、投資の価値が生ドルで毎年どのように変化したかを視覚化するのに役立ちますが、投資の成長率を理解することにもっと興味があると仮定しましょう。

この場合、y 軸を対数スケールに変換すると便利です。

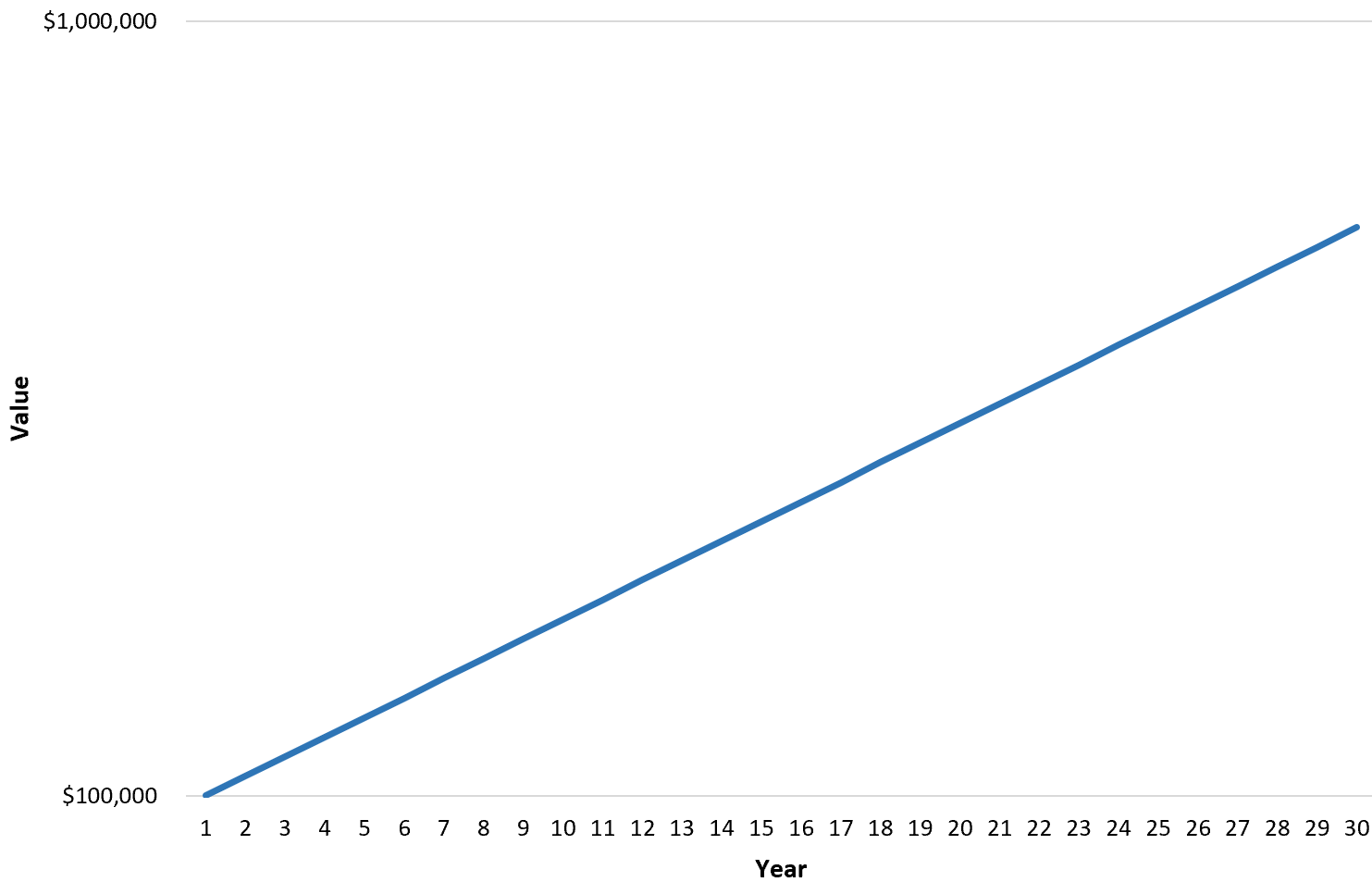
このグラフを使用すると、投資価値の変化率が 30 年間にわたって毎年一貫していることがわかります。

注: 対数スケールの使用は、変数が指数関数的に増加している場合、一定期間にわたる変数の変化率を視覚化するのに便利です。これは、期間の終わりに近づく値の変化が変化を覆い隠す傾向があるためです。期末付近の値。始まり。

追加リソース

次のチュートリアルでは、さまざまな統計ソフトウェアで対数スケールのグラフを作成する方法を説明します。

R で対数スケールを作成する方法
Python で対数スケールを作成する方法
Excel で対数スケールを作成する方法