対数回帰

この記事では、対数回帰とは何か、またその実行方法について説明します。さらに、概念を完全に理解するために対数回帰の例を見ることができます。

対数回帰とは何ですか?

対数回帰は、方程式に対数を含む回帰モデルです。具体的には、対数回帰では、独立変数の対数が取得されます。したがって、対数回帰モデルの方程式は y=a+b·ln(x) となります。

対数回帰は、サンプル データが対数曲線を形成している場合に、回帰モデルをサンプル データによりよく適合させるために回帰モデルを適合させるのに非常に役立ちます。以下では、対数回帰をいつ実行する必要があるかを見ていきます。

したがって、対数回帰は、指数回帰や多項式回帰と同様、非線形回帰の一種です。

対数回帰式

対数回帰モデルでは、独立変数の対数を計算します。したがって、対数回帰の方程式の式はy=a+b・ln(x) となります。

金：

• 

  は従属変数です。

• 

  は独立変数です。

• 

  は回帰係数です。

y=a+b・ln(x) は実際には直線の方程式ですが、元の変数 x と y を参照する代わりに、変数 ln(x) と y を参照していることに注意してください。

対数回帰はいつ行うべきですか?

サンプルデータのグラフが対数曲線である場合、つまり点のプロットが対数関数のグラフに類似している場合、対数回帰を実行する必要があります。

以下の散布図を見てください。線形回帰モデルがデータセットに当てはめられています。ご覧のとおり、この線はデータの悪い近似ではありませんが、注意すると、グラフの終わりよりもグラフの最初の方が値が速く増加するため、線は観測結果と完全には一致しません。 。

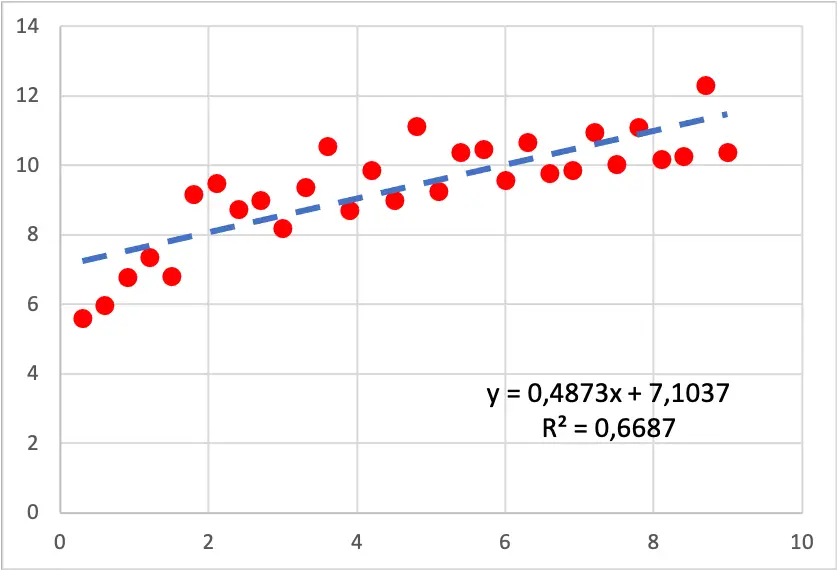
データが対数曲線に従っているように見えるため、対数回帰モデルを作成してみる価値はあります。対数回帰モデルから得られた結果は次のとおりです。

前のグラフからわかるように、結果として得られる対数回帰モデルはサンプル データによりよく適合しています。実際、決定係数は 66.87% から 80.05% に増加したため、モデルはデータ サンプルをより適切に説明できるようになりました。したがって、この場合は、ロジスティック回帰を使用して、データ値を近似する式を見つけることをお勧めします。

他のタイプの非線形回帰

非線形回帰の最も一般的なケースは次の 3 つです。

• 対数回帰: 独立変数の対数が取得されます。
• 指数回帰: 独立変数は方程式の指数です。
• 多項式回帰: 回帰モデル方程式は多項式の形式です。