統計における連続性補正の簡単な説明
連続性補正は、連続分布を使用して離散分布を近似する場合に適用されます。一般に、正規分布を使用して二項分布を近似したい場合に使用されます。
1 回の試行での成功確率がpであるとすると、二項分布はn回の試行でx の成功を達成する確率を示していることを思い出してください。二項分布による確率に関する質問に答えるには、単に二項分布計算機を使用することもできますが、連続性補正を備えた正規分布を使用して確率を近似することもできます。
連続性補正は、離散 x 値に0.5 を加算または減算することを指す名前です。
たとえば、コインを 100 回投げる間に、コインが 45 回以下で表になる確率を求めたいとします。つまり、P(X ≤ 45) を見つけたいのです。正規分布を使用して二項分布を近似するには、代わりに P(X ≤ 45.5) を見つけます。
次の表は、検索しようとしている確率のタイプに応じて、いつ 0.5 を加算または減算する必要があるかを示しています。
| 二項分布を使用する | 連続性補正を伴う正規分布の使用 |
|---|---|
| X = 45 | 44.5 < X < 45.5 |
| X ≤ 45 | X < 45.5 |
| X < 45 | X < 44.5 |
| X ≥ 45 | X > 44.5 |
| X > 45 | X > 45.5 |
注記:
n*p と n*(1-p) が両方とも 5 以上である場合にのみ、正規分布に連続性補正を適用して二項分布を近似することが適切です。
たとえば、n = 15 および p = 0.6 と仮定します。この場合:
n*p = 15 * 0.6 = 9
n*(1-p) = 15 * (1 – 0.6) = 15 * (0.4) = 6
これらの数値は両方とも 5 以上であるため、このシナリオでは連続性補正を適用しても問題ありません。
次の例は、正規分布に連続性補正を適用して二項分布を近似する方法を示しています。
連続性補正の適用例
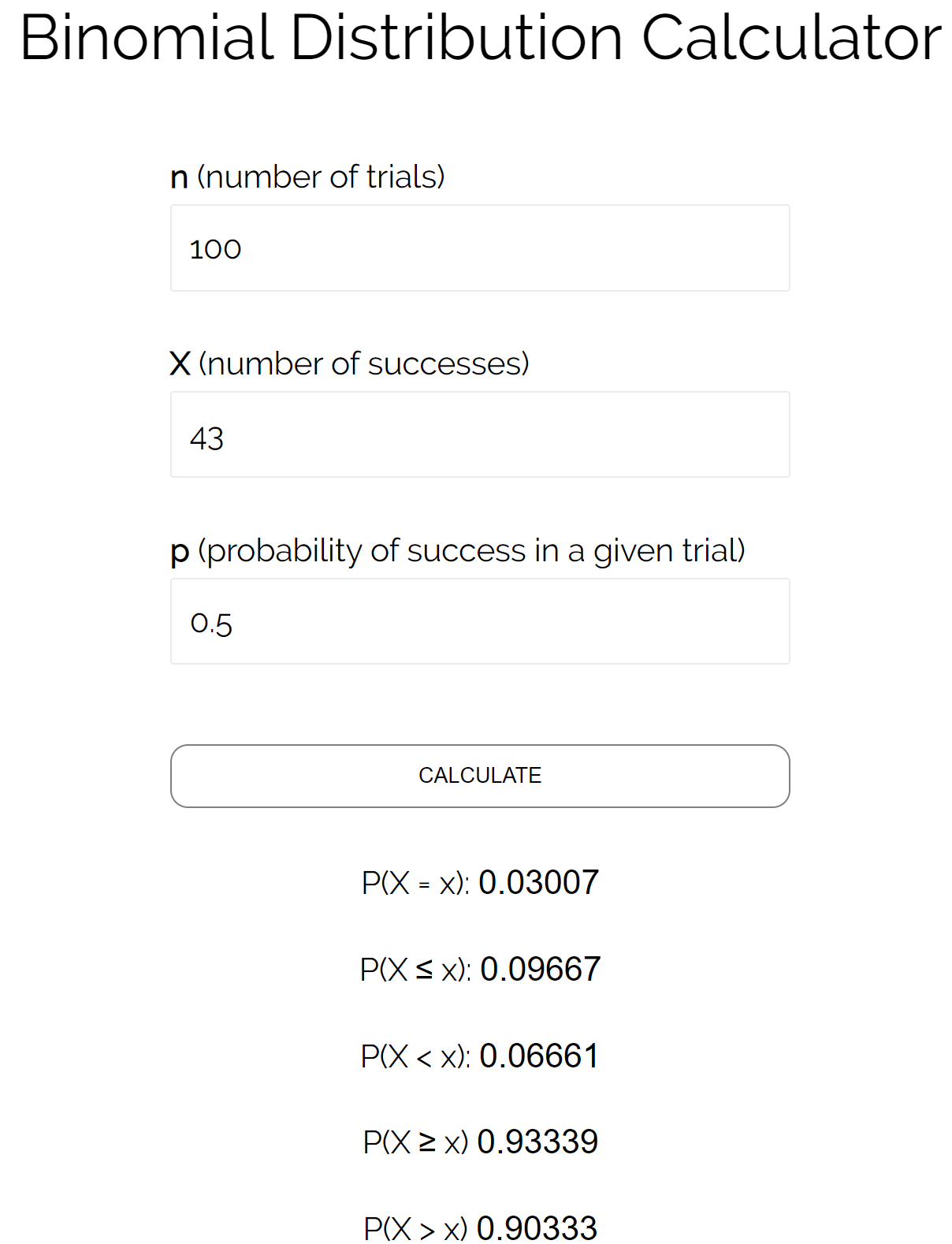
コインを 100 回投げて 43 回以下で表が出る確率を知りたいとします。この場合:
n = 試行回数 = 100
X = 成功数 = 43
p = 特定の試行における成功確率 = 0.50
これらの数値を二項分布計算ツールに代入すると、コインが 43 回以下の表に当たる確率が0.09667であることがわかります。
正規分布に連続性補正を適用して二項分布を近似するには、次の手順を使用できます。
ステップ 1: n*p と n*(1-p) が両方とも 5 以上であることを確認します。
n*p = 100*0.5 = 50
n*(1-p) = 100*(1 – 0.5) = 100*0.5 = 50
どちらの数値も 5 以上であるため、続行できます。
ステップ 2: 0.5 を加算するか減算するかを決定します。
上の表を参照すると、X ≤ 43 の形式で確率を扱う場合、 0.5を追加する必要があることがわかります。したがって、P(X< 43.5) が見つかります。
ステップ 3: 二項分布の平均 (μ) と標準偏差 (σ) を求めます。
μ = n*p = 100*0.5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
ステップ 4: 前のステップで見つかった平均と標準偏差を使用して Z スコアを見つけます。
z = (x – μ) / σ = (43.5 – 50) / 5 = -6.5 / 5 = -1.3。
ステップ 5: Z テーブルを使用して、Z スコアに関連付けられた確率を見つけます。
表 Z によると、z = -1.3 に関連する確率は0.0968です。
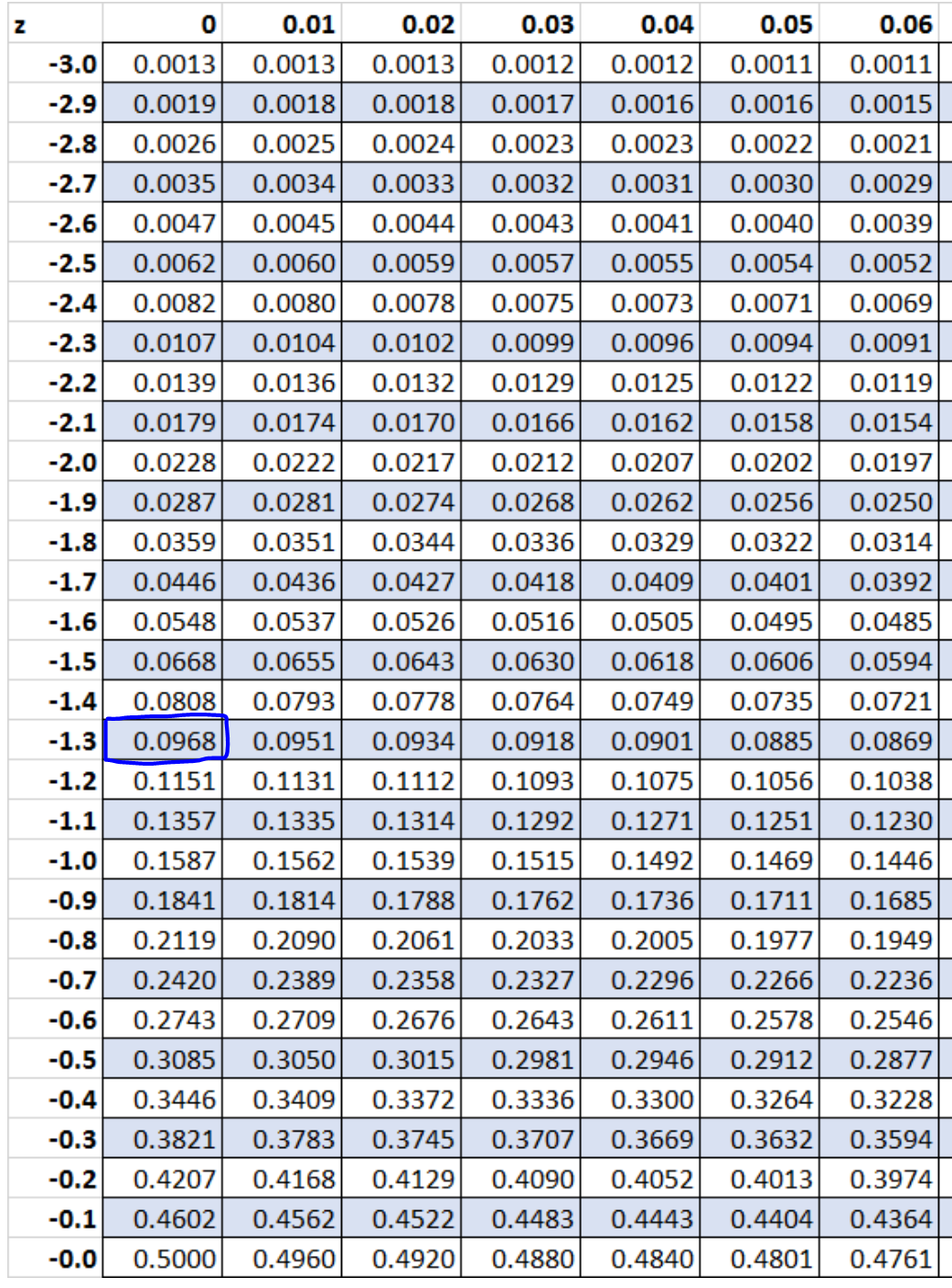
したがって、二項分布を使用して求めた正確な確率は0.09667でしたが、正規分布による連続性補正を使用して求めたおおよその確率は0.0968でした。これら 2 つの値は非常に近いです。
連続性補正を使用する場合
最新の統計ソフトウェアが存在し、計算を手動で行う必要がある前は、離散分布を含む確率を見つけるために連続性補正がよく使用されていました。現在、私たちは通常、ソフトウェアや計算機に確率を計算してもらうことができるため、確率の計算において連続性補正が果たす役割はそれほど大きくありません。
むしろ、これは、二項分布と正規分布の関係を説明し、連続性補正を適用することで正規分布が二項分布に近似できることを示すために、統計コースで扱われるトピックにすぎません。
導通補正計算機
連続性補正計算ツールを使用して、正規分布に連続性補正を自動的に適用し、二項確率を近似します。