層化抽出法

この記事では、層化サンプリングとは何か、またその実行方法について説明します。ここでは、層化サンプリングのサブタイプについて説明し、最後に層化サンプリングの長所と短所について説明します。

層化サンプリングとは何ですか?

層化サンプリングは、母集団をグループ (層と呼ばれます) に分割することによってサンプルの要素を選択するために使用される統計的手法です。つまり、層化サンプリングでは、母集団がいくつかの層に分割され、各層からの個人がランダムに選択されて研究サンプル全体が形成されます。

層は同質の集団です。言い換えれば、層内の個人は他の層とは異なる独自の特性を持っています。したがって、個人は 1 つの階層にのみ属することができます。

層化サンプリングは、母集団が互いに大きく異なる非常に同種のグループで構成されている場合に非常に役立ちます。

論理的には、すべての層のサイズの合計により、統計上の母集団のサイズが求められます。

同様に、各層で選択されたサンプル サイズの合計は、統計調査の合計サンプル サイズと等しくなります。

通常、大文字と小文字を区別して、それぞれ母集団またはサンプルを指定します。

層化サンプリングの方法

層化サンプリングを実行する手順は次のとおりです。

1. 対象集団を定義します。
2. 変数の階層化と、存在する階層の数を選択します。
3. 母集団の各要素がどの層に属しているかを特定します。
4. サンプルの一部となる各層のサイズを計算します。
5. 研究サンプルに属する各層から要素をランダムに選択します。各層について、前のステップで決定したのと同じ数の要素を選択する必要があります。

サンプル内で各層が表すサイズは、層のサイズだけでなく、層別サンプリングのタイプにも依存することに注意してください。次に、層別サンプリングの種類と各層のサンプルサイズの計算方法を例を用いて説明します。

層化サンプリングの種類

層化サンプリングの定義を理解したところで、層化サンプリングにはいくつかの種類があり、次のように分類されることを理解する必要があります。

• 比例層化サンプリング
• 均一な層化サンプリング
• サンプリングは最適です

それぞれの意味をよりよく理解するために、層別サンプリングの各タイプについて以下で詳しく説明します。

比例層化サンプリング

層化比例サンプリング(比例配分サンプリング) では、研究サンプルの一部である各層の要素の数は、各層のサイズに比例します。

したがって、ある層が別の層よりも大きい場合、最終サンプルにはその層からの要素がより多く含まれることになります。一方、ある層が別の層よりも小さい場合、統計分析サンプル内のこの層の要素は少なくなります。

このタイプの層別サンプリングは、層のサイズが異なり、より大きな層からの要素をより多くサンプルに含めたい場合に便利です。

サンプル内に含まれる各層の要素の数を計算するには、各層のサイズをすべての層のサイズの合計で割る必要があります。結果はサンプルに含まれる層の割合となるため、これに希望のサンプル サイズを掛ける必要があります。

金

は必要なサンプルの合計サイズです。

層内の要素の数

サンプルに含まれる、

層のサイズ

、 そして

母集団内の要素の総数。

たとえば、従業員 150 人の会社で 50 人のサンプルを採取し、従業員の年齢に基づいてデータを層別化して調査したいと考えたとします。データは次のように分類できます。

• 20歳～29歳まで 35名
• 30歳～39歳まで 57名
• 40歳～49歳 従業員42名
• 50歳～59歳：16名

したがって、データを比例的に階層化すると、サンプリングは次のようになります。

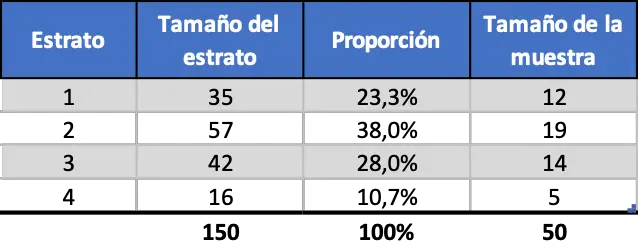
均一な層化サンプリング

均一層化サンプリング、または均一付加サンプリングでは、研究サンプルの一部である各層の要素の数は等しいです。

したがって、このタイプのサンプリングでは、各層の重みは同じになります。ある層の個体数が他の層より多いか少ないかに関係なく、サンプル内ではすべてが同じ数の個体で表されます。

この場合、各層の要素のサイズを計算するには、必要なサンプル サイズを既存の層の数で割る必要があります。つまり、次の式を使用する必要があります。

金

は必要なサンプルの合計サイズです。

層内の要素の数

誰がサンプルに含まれるのか、そして

人口が分割されている層の数。

前の例に従って、50 人の労働者のサンプルが必要で、合計 4 つの異なる層があったため、各層のサンプル サイズは次のようになります。

結果は 10 進数であり、50 ワーカーに達するまで、一部の階層には 12 人のワーカーが存在し、他の階層には 13 人のワーカーが存在します。したがって、均一層化サンプリングは次のようになります。

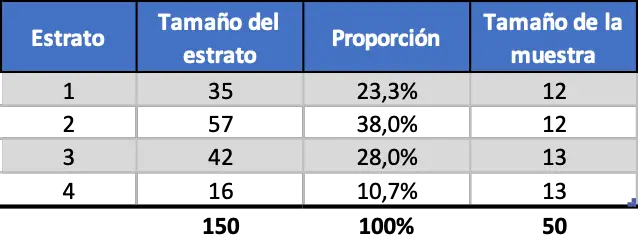
ご覧のとおり、各層のサンプル サイズはそれぞれの割合とは無関係です。

最適な層化サンプリング

最適な層別サンプリングでは、各層の要素の数は各層の変動に比例して決まります。

したがって、変動が大きい層のサンプル サイズは大きくなり、逆も同様で、変動が小さい層のサンプル サイズは小さくなります。

各層の要素の数が統計調査サンプルの一部となるかを決定する式は次のとおりです。

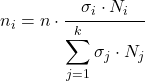
金

は必要なサンプルの合計サイズです。

層内の要素の数です

サンプルに含まれる、

層の標準偏差 (または典型偏差) です。

、 そして

地層のサイズです

。

層化サンプリングの長所と短所

層化サンプリングには次のような利点と欠点があります。

アドバンテージ	短所
これにより、人口全体だけでなく、特定の各層についても統計的に研究することが可能になります。	これは実装が複雑なサンプリング方法です。
層化サンプリングによって生じるサンプリング誤差は、常に単純なランダムサンプリングの誤差以下になります。	これは時間がかかり、したがって高価なサンプリングプロセスです。
これにより、母集団に関する研究者の知識を活用することができます。	分析されたサンプルを層別化するには、サンプルに関する多くの情報が必要です。
層化サンプリングでは、各層の少なくとも 1 つの要素がサンプルに含まれていることを確認します。	サンプリングを実行するには、各層の割合を知る必要があります。

層化サンプリングの主な特徴は、母集団を分割した各グループまたは階層を統計的に分析するために使用されることです。もちろん、このタイプのサンプリングを使用して母集団全体を研究することもできます。さらに、データの階層化の利点は、階層が互いに異なる場合に大きくなります。

それどころか、サンプリングを実行できるようにデータを層化するという事実は、サンプリングの複雑さの増加を意味し、層化サンプリングは他のタイプのサンプリングと比較して実行がより複雑になります。この特性は、層別化を正しく行うには時間がかかるため、サンプルの作成に費用がかかることも意味します。

層化抽出のもう1つの欠点は、研究対象とする母集団について多くの情報が必要になることですが、単純無作為抽出などの他のタイプの抽出では必要ありません。ただし、研究者がその分野で豊富な知識を持っていれば、この欠点は軽減できます。

最後に、層化サンプリングでは、各層の要素が確実に含まれるため、他のタイプのサンプリングよりも母集団をより代表するサンプルが得られます。対照的に、他のサンプルでは、結果として得られるサンプルにどの層の元素も含まれていない可能性があります。