平均値、中央値、最頻値
この記事では、平均値、中央値、最頻値について説明します。平均値、中央値、最頻値を取得する方法、それらの用途、およびこれら 3 つの統計的尺度の違いについて学びます。さらに、最後にあるオンライン計算機を使用して、統計サンプルの平均、中央値、最頻値を計算することができます。
平均値、中央値、最頻値とは何ですか?
平均、中央値、最頻値は中心位置の統計的尺度です。言い換えれば、平均値、中央値、最頻値は統計サンプルを定義するのに役立つ値であり、特にその中心値が何であるかを示します。
平均値、中央値、最頻値は次のように定義されます。
- 平均: サンプル内のすべてのデータの平均です。
- Median : これは、最小値から最大値の順に並べられたすべてのデータの中央の値です。
- モード: これは、データセット内で最も繰り返される値です。
これら 3 つの統計的尺度については、以下で詳しく説明します。
半分
平均を計算するには、すべての値を加算し、データの総数で割ります。したがって、平均の式は次のようになります。

👉以下の計算機を使用して、任意のデータセットの平均、中央値、最頻値を計算できます。
平均記号は、文字 x の上にある水平の帯です。
![]()
平均値記号を使用して標本の平均と母集団の平均を区別することもできます。標本の平均は記号で表されます。
![]()
、母集団の平均はギリシャ文字を使用します
![]()
平均は、算術平均または平均とも呼ばれます。さらに、統計分布の平均は、その数学的期待値と等価です。
平均的な例
- 学生は学年中に次の成績を達成しました:数学で 9、言語で 7、歴史で 6、経済で 8、科学で 7.5。あなたのすべての成績の平均はいくらですか?
算術平均を求めるには、すべての成績を合計し、コース内の科目の総数である 5 で割る必要があります。したがって、算術平均の公式を適用します。

データを式に代入し、算術平均を計算します。
![]()
ご覧のとおり、算術平均では、各値に同じ重みが割り当てられます。つまり、各データは全体の中で同じ重みを持ちます。
中央値
中央値は、すべてのデータを最小値から最大値の順に並べた中央の値です。言い換えれば、中央値は順序付けされたデータセットを 2 つの等しい部分に分割します。
中央値の計算は、データの総数が偶数か奇数かによって異なります。
- データの総数が奇数の場合、中央値はデータの中央に位置する値になります。つまり、ソートされたデータの位置 (n+1)/2 にある値です。
- データ ポイントの合計数が偶数の場合、中央値は中央に位置する 2 つのデータ ポイントの平均になります。つまり、順序付けされたデータの位置 n/2 および n/2+1 で見つかる値の算術平均です。
![]()
![]()
金
![]()
サンプル内のデータ項目の総数です。
Meという用語は、値がすべての観測値の中央値であることを示す記号としてよく使用されます。
👉以下の計算機を使用して、任意のデータセットの平均、中央値、最頻値を計算できます。
中央値の例
- 次のデータの中央値を見つけます: 3、4、1、6、7、4、8、2、8、4、5
計算を行う前に最初に行うことは、データを分類することです。つまり、数値を最小値から最大値の順に並べます。
![]()
この場合、観測値は 11 個あるため、データの合計数は奇数になります。したがって、次の式を適用して中央値の位置を計算します。
![]()
したがって、中央値は 6 番目の位置にあるデータとなり、この場合は値 4 に対応します。
![]()
ファッション
統計において、最頻値はデータ セット内で最も高い絶対頻度を持つ値、つまり、最頻値はデータ セット内で最も繰り返される値です。
したがって、統計データ セットの最頻値を計算するには、サンプル内で各データ要素が出現する回数を数えるだけで、最も多く繰り返されたデータが最頻値となります。
モードは、統計モードまたは最頻値とも言えます。同様に、データが間隔にグループ化される場合、最も繰り返される間隔がモーダル間隔またはモーダル クラスになります。
一般に、 Moという用語は統計モードの記号として使用されます。たとえば、分布モード X は Mo(X) です。
最も繰り返される値の数に応じて、次の 3 種類のモードを区別できます。
- ユニモーダル モード: 最大繰り返し回数を持つ値は 1 つだけです。たとえば、[1、4、2、4、5、3]。
- バイモーダル モード: 最大繰り返し回数は 2 つの異なる値で発生し、両方の値が同じ回数繰り返されます。たとえば、[2、6、7、2、3、6、9]。
- マルチモーダル モード: 3 つ以上の値が同じ最大繰り返し回数を持ちます。たとえば、[3、3、4、1、3、4、2、1、4、5、2、1]。
👉以下の計算機を使用して、任意のデータセットの平均、中央値、最頻値を計算できます。
ファッションの例
- 次のデータセットのモードは何ですか?
![]()
番号の順序が間違っているので、最初に番号を並べ替えます。このステップは必須ではありませんが、ファッションを見つけやすくなります。
![]()
2 と 9 という数字は 2 回現れますが、5 という数字は 3 回繰り返されます。したがって、データ系列の最頻値は 5 です。
![]()
平均値、中央値、最頻値の計算問題を解決
平均値、中央値、最頻値が何であるかは理解できたので、以下ではこれらの統計的尺度について詳しく説明し、それらがどのように計算されるかを正確に確認できるようにします。
- 次の統計データ セットの平均、中央値、最頻値を求めます。
![]()
![]()
データの平均を求めるには、すべてを合計し、データの総数である 30 で割る必要があります。
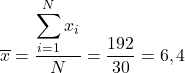
次に、サンプルの中央値を調べてみましょう。したがって、すべての数値を昇順に並べます。
![]()
![]()
この場合、データの総数は偶数であるため、中央値が見つかる 2 つの中心位置を計算する必要があります。このために、次の 2 つの公式を使用します。
![]()
![]()
したがって、中央値は 15 番目と 16 番目の位置の間にあり、それぞれ値 6 と 7 に対応します。より正確には、中央値はこれらの値の平均に相当します。
![]()
最後に、モードを見つけるには、各数字が出現する回数をすべて数えるだけです。ご覧のとおり、6 番と 8 番が合計 4 回出現し、これが最大の繰り返し回数になります。したがって、この場合は二峰性モードであり、2 つの数値がデータセットのモードになります。
![]()
平均値、中央値、最頻値の計算機
統計サンプルのデータを次のオンライン計算機に入力して、平均値、中央値、最頻値を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。