幾何分布の概要
幾何分布は、一連のベルヌーイ試行で最初の成功を経験する前に、一定回数の失敗を経験する確率を表します。
ベルヌーイ試行は、「成功」または「失敗」の 2 つの結果しか考えられない実験であり、実験が実行されるたびに成功の確率は同じです。
ベルヌーイのエッセイの例としては、コイントスがあります。コインは 2 つの表にのみ着地できます (表を「ヒット」、裏を「失敗」と呼びます)。コインが公正であると仮定すると、各フリップでの成功確率は 0.5 です。
確率変数X が幾何分布に従う場合、最初の成功を経験する前にk回の失敗を経験する確率は、次の式で求められます。
P(X=k) = (1-p) kp
金:
- k:最初の成功までの失敗回数
- p:各試行の成功確率
たとえば、表が出るまで公正なコインを何回投げなければならないかを知りたいとします。上記の式を使用して、0、1、2、3 回などの失敗が発生する確率を決定できます。コインが表になる前に:
注:最初のトスでコインが表になった場合、コインの「失敗」は 0 になります。
P(X=0) = (1-.5) 0 (.5) = 0.5
P(X=1) = (1-.5) 1 (.5) = 0.25
P(X=2) = (1-.5) 2 (.5) = 0.125
P(X=3) = (1-0.5) 3 (0.5) = 0.0625
コイン投げの確率を無限大まで計算できます。次に、この確率分布を視覚化するための単純なヒストグラムを作成します。
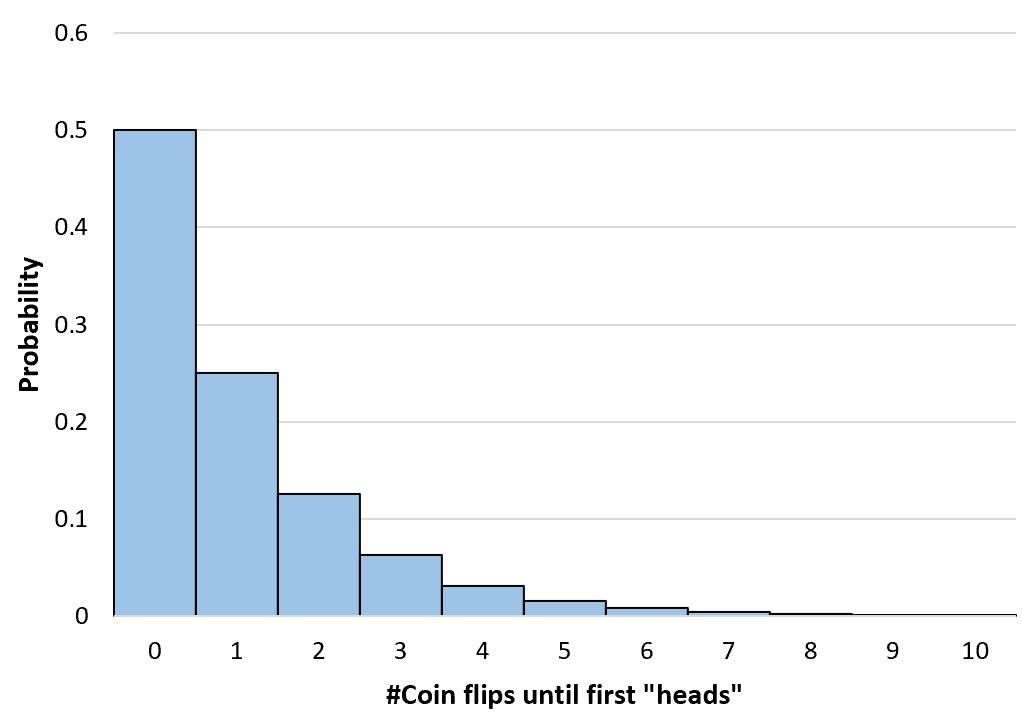
累積幾何確率の計算
最初の成功までに k 以下の失敗を経験する累積確率は、次の式で求められます。
P(X≤k) = 1 – (1-p) k+1
金:
- k:最初の成功までの失敗回数
- p:各試行の成功確率
たとえば、コインが最終的に表になるまでに 3 回以下の「ミス」が発生する確率を知りたいとします。この確率を計算するには次の式を使用します。
P(X≤3) = 1 – (1-0.5) 3+1 = 0.9375
同様の式を使用して、各累積確率を計算できます。
P(X≤0) = 1 – (1-.5) 0+1 = 0.5
P(X≤1) = 1 – (1-0.5) 1+1 = 0.75
P(X≤2) = 1 – (1-0.5) 2+1 = 0.875
これらの累積確率は、コインを投げる回数を無限に増やして計算できます。次に、ヒストグラムを作成して、この累積確率分布を視覚化できます。
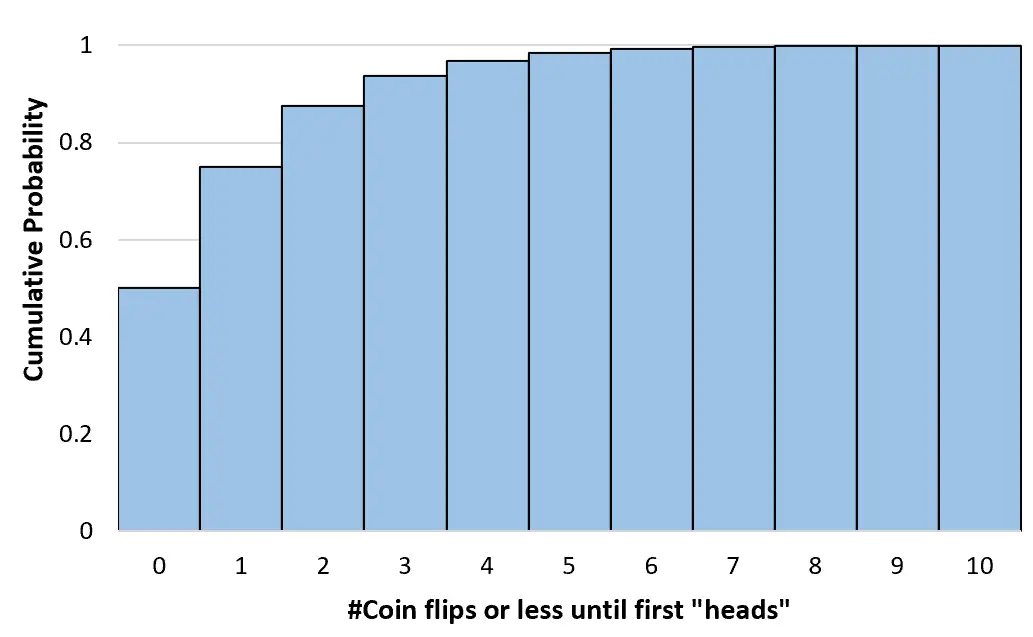
幾何分布の性質
幾何分布には次の特性があります。
分布の平均は(1-p) / pです。
分布の分散は(1-p) / p 2です。
例えば:
コインが裏になるまでに表が出る平均回数は、 (1-p) / p = (1-.5) / .5 = 1となります。
表に着地するまでのトス数の分散は、(1-p)/ p2 =(1-.5)/ となります。 52 = 2 。
幾何分布の練習問題
次の練習問題を使用して、幾何分布の知識をテストしてください。
注:これらの質問に対する答えを計算するには、幾何分布計算ツールを使用します。
問題 1
質問:研究者は図書館の外で待機し、特定の法律を支持するかどうかを人々に尋ねます。特定の人が法則を支持する確率は p = 0.2 です。研究者が話しかけた 4 人目の人がその法律を最初に支持する確率はどれくらいですか?
答え:最初の成功までの「失敗」の数、つまり、最初の人が法則を支持するまでその法則を支持しない人の数は 3 です。したがって、p = 0.2 および x で幾何分布計算を使用すると、 = 3 回の失敗の場合、 P(X=3) = 0.10240であることがわかります。
問題 2
質問:研究者は図書館の外で待機し、特定の法律を支持するかどうかを人々に尋ねます。特定の人が法則を支持する確率は p = 0.2 です。研究者がこの法律を支持する人を見つけるために 4 人以上の人と話をしなければならない確率はどれくらいですか?
回答: p =0.2 および x = 4 回の失敗で幾何分布計算を使用すると、 P(X>4) = 0.32768であることがわかります。
問題 3
質問:研究者は図書館の外で待機し、特定の法律を支持するかどうかを人々に尋ねます。特定の人が法則を支持する確率は p = 0.2 です。この法律を支持する人を見つけるまで、研究者は何人の人と話す必要があると予想されますか?
答え:幾何分布の平均は(1-p) / pであることを思い出してください。この状況では、平均は (1-.2) / .2 = 4となります。