従属変数と独立変数
この記事では、従属変数と独立変数について説明します。したがって、従属変数と独立変数の違い、どれが従属変数でどれが独立変数であるかを知る方法がわかり、さらに、このタイプの変数の例がいくつか示されています。
従属変数と独立変数とは何ですか?
従属変数とは、その値が別の変数(独立変数)に依存する変数です。したがって、従属変数と独立変数の違いは、独立変数は他の変数に依存しないのに対し、従属変数は独立変数の値に依存することです。
グラフでは、独立変数は横軸 (横軸) の文字xで表され、従属変数は縦軸 (縦軸) の文字yで表されます。
たとえば、統計研究で取得した成績と費やした勉強時間の関係を分析する場合、費やした勉強時間は独立変数であり、取得した成績は従属変数です。取得できる成績は勉強時間に依存し、その逆はありません。
従属変数と独立変数の例
前のセクションでは、従属変数と独立変数の定義を見てきました。そこで、その意味をよりよく理解するために、このタイプの変数の 10 個の例を見ていきます。
- 勉強に費やした時間 (独立変数) は、取得した成績 (従属変数) に影響します。
- 製品の価格 (独立変数) は、その製品を購入する意欲のある人の数 (従属変数) を変化させます。
- 人の健康 (従属変数) は食事 (独立変数) に依存します。
- 人の心拍数 (従属変数) は、心拍数の高さ (独立変数) の影響を受けます。
- 周囲温度 (独立変数) は森林火災の数 (従属変数) に影響します。
- 顧客満足度 (従属変数) は、提供されるサービスの品質 (独立変数) に応じて変化します。
- 製品の広告 (独立変数) は、その製品の販売数 (従属変数) に影響を与えます。
- ある国が排出する汚染物質の量(従属変数)は、その国の工業生産(独立変数)に依存します。
- タクシー運転手の給与(従属変数)は、乗車回数(独立変数)に応じて変化します。
- 都市の住民の数 (独立変数) は、都市内のタクシーの台数 (従属変数) に関連付けられています。
調査に応じて、変数は関係の原因または結果として機能するため、変数はコンテキストに応じて依存または独立することに留意してください。
従属変数と独立変数の演習
次の場合、どちらが従属変数でどちらが独立変数でしょうか?
- 都市の住民の数 – 公共バスの数
- 車両の年式 – 車両の状態
- 蚊の数 – 周囲温度
- 月別の雨の日の数 – 傘の需要
- 従属変数: 公共バスの数 – 独立変数: 都市の住民の数
- 従属変数: 車両の状態 – 独立変数: 車両の使用年数
- 従属変数: 蚊の数 – 独立変数: 周囲温度
- 従属変数: 傘の需要 – 独立変数: 1 か月あたりの雨の日の数
数学における従属変数と独立変数
数学では、通常、原因と結果の関係は、独立変数と従属変数を使用してモデル化されます。したがって、関数は従属変数と独立変数の間に存在する数学的関係を定義します。
![]()
従属変数は通常、文字yで表され、一方、独立変数を示すには通常、文字xが使用されます。
たとえば、関数y=2x は、独立変数x が1 単位増加すると、従属変数yが 2 倍増加することを示します。
数学関数の詳細については、パートナー Web サイトfunction.xyzにアクセスしてください。
統計における従属変数と独立変数
ただし、実際には、独立変数の値が同じでも従属変数の値が異なる場合があるため、正確な数学関数で定義できる 2 つの変数間の関係を見つけることは非常に困難です。
たとえば、勉強量を増やすと成績が下がる場合や、逆に勉強量を減らすと成績が上がる場合があります。したがって、取得する成績に影響を与えるのは、勉強に費やした時間数だけではなく、試験の難易度や学習内容の難易度によっても異なります。
このため、統計学では通常、2 つの変数 (一方が独立変数、もう一方が従属変数) の間に関係があるかどうかを判断するために多くの実験が実行されます。次に、得られた結果をグラフで表現して、変数がリンクされているかどうかを確認し、リンクされている場合には、それらの関係の種類 (正、負、線形、指数など) を確認できます。
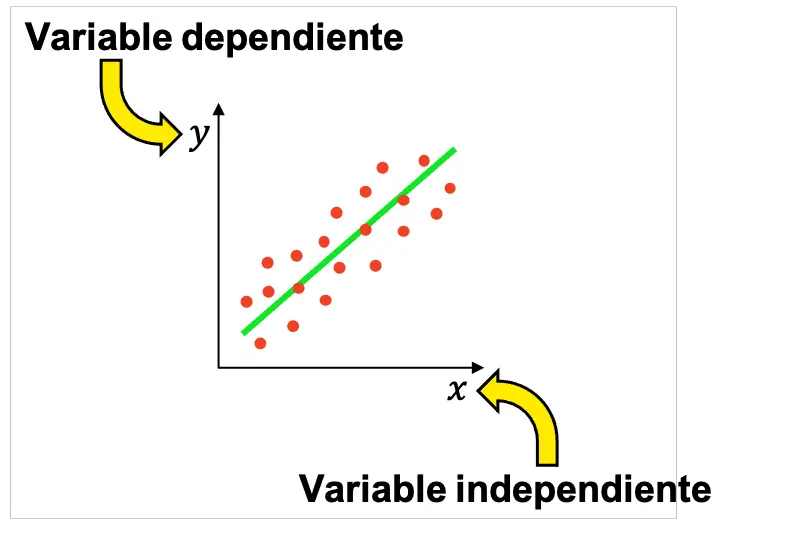
最も基本的な統計研究は 1 つの独立変数と 1 つの従属変数を使用して実行されますが、調査には複数の独立変数が存在する可能性があることに留意してください。
統計的研究が実行されると、数学関数を計算して近似を行い、変数間の関係をモデル化できます。したがって、通常は統計モデルが最初に作成され、次に数学モデルが作成されます。