指数分布
この記事では、統計における指数分布とは何か、またそれが何に使用されるのかについて説明します。同様に、指数分布の特性、その式、グラフ、および解決済みの演習がわかります。さらに、オンラインの指数分布計算ツールを使用して任意の確率を計算できます。
指数分布とは何ですか?
指数分布は、ランダム現象の発生の待ち時間をモデル化するために使用される連続確率分布です。
より正確には、指数分布を使用すると、ポアソン分布に従う 2 つのイベント間の待ち時間を記述することができます。したがって、指数分布はポアソン分布と密接に関係しています。
指数分布には、ギリシャ文字 λ で表される特徴的なパラメーターがあり、特定の期間内に調査対象のイベントが発生すると予想される回数を示します。
![]()
同様に、指数分布は障害が発生するまでの時間をモデル化するためにも使用されます。したがって、指数分布は信頼性と生存理論においていくつかの用途があります。
指数分布の例
指数分布の定義を理解したところで、概念をより深く理解するために、このタイプの分布の例をいくつか見てみましょう。
指数分布の例:
- コールセンターでの 2 つの通話間の経過時間。
- 特定の通りで無料のタクシーが通過するまでに待たなければならない時間。
- 新しい客が店に入るまでの待ち時間。
- 2 人の異なるユーザーが Web ページにアクセスするまでに経過する時間。
- 空港で、ある飛行機が離陸してから別の飛行機が出発するまでの経過時間。
指数分布式
指数分布確率の計算を定義する密度関数の式は、λ に e の負の λ 乗と x を乗算した値に等しくなります。
つまり、指数分布確率を計算する式は次のようになります。

👉以下の計算機を使用して、指数分布に従う変数の確率を計算できます。
一方、指数分布の累積確率を計算する式は次のとおりです。
![]()
指数分布グラフ
このセクションでは、指数分布の密度関数と分布関数のグラフ表示を確認できます。
以下に、指数分布の密度関数のグラフがパラメーター λ の値に応じてどのように変化するかを示します。
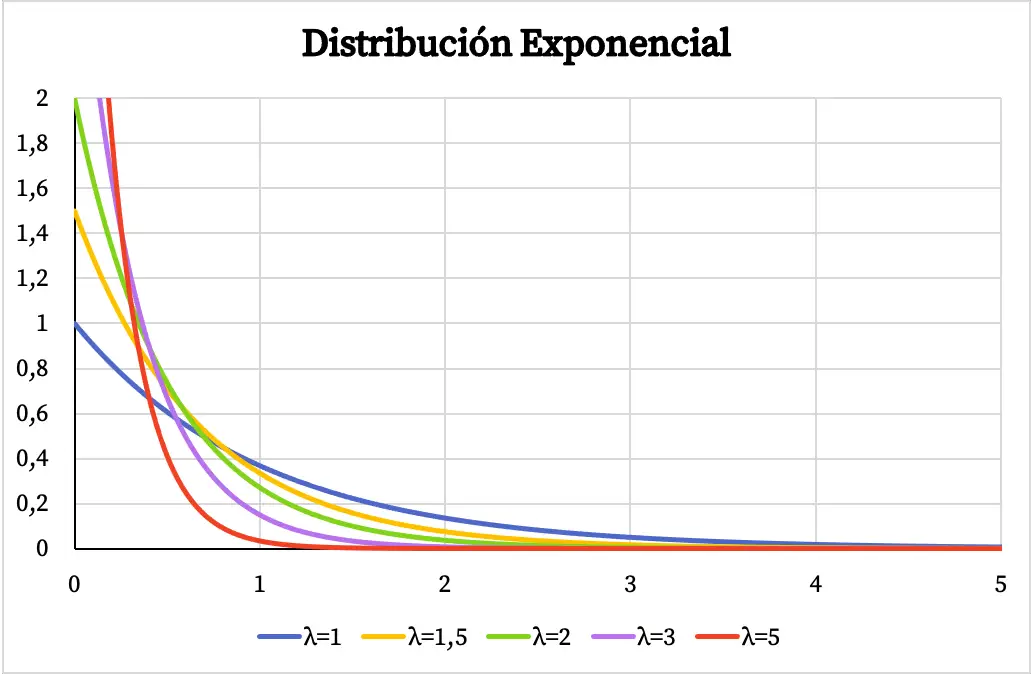
同様に、次のグラフに示すように、指数分布の累積確率関数もパラメーター λ の値に依存します。
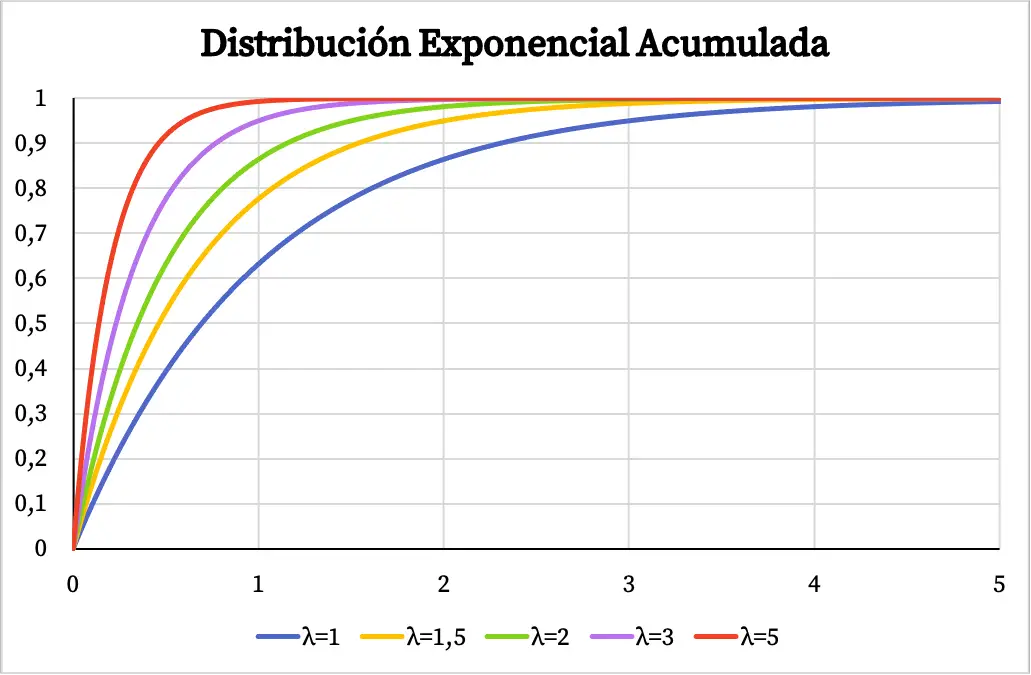
指数分布に関する演習を解決しました
- 平均して、λ=1 ユーザー/分が特定の Web ページにアクセスします。 2 人のユーザーが入場するまでの時間が 3 分である確率はいくらですか?そしてそれが 2 分以下になる確率は?
イベントが発生した瞬間 (Web ページへのユーザーのエントリ) から同じイベントが再び発生するまでの経過時間を研究しているため、この問題の確率変数を定義する分布は指数分布です。
![]()
したがって、2 人の異なるユーザーが入場するまでの経過時間が 3 分である確率を計算するには、密度関数の公式 (上記を参照) を適用する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4eb2d6e5190f313d74831763613683ec_l3.png)
一方、累積確率を決定するには、指数分布の分布関数式を使用する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5ff6ef636fd31aec708b387669a68b93_l3.png)
指数分布の特徴
指数分布には次のような特徴があります。
- 指数分布には、特定の期間内に調査対象の現象が発生すると予想される回数を示す特性パラメータ λ があります。
![]()
- 指数分布は負の値を取ることができないため、指数分布の領域はゼロ以上のすべての実数で構成されます。
![]()
- 指数分布の平均は、特性パラメータ λ で割った値に等しくなります。
![]()
- 指数分布の分散は平均の 2 乗であるため、指数分布の分散は係数 λ の 2 乗に相当します。
![]()
- λ の値が何であっても、指数分布の非対称係数は常に 2 に等しくなります。
![]()
- 同様に、指数分布の尖度係数は常に 9 に等しくなります。
![]()
- 指数分布の密度関数の式は次のとおりです。
![]()
- 一方、指数分布の累積確率関数の式は次のとおりです。
![]()
- 指数分布は、メモリ不足の特性を持つ数少ない確率分布の 1 つです。この特性は、前のイベントの発生が将来そのイベントが発生する確率に影響を与えないことを意味します。たとえば、指数分布では、新しいユーザーが 1 分以内に Web ページにアクセスする確率は、ユーザーが入ったばかりか、それ以来入ってきたユーザーがいないかには依存しません。 10分以上。
![P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p>
</p>
<h2 class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6f7c755e5b48eb203c51c97d7bc7ec7d_l3.png) 指数分布計算機
指数分布計算機
パラメータλの値とxの値を次の計算機に入力して、確率を計算します。計算する確率を選択し、小数点区切りとしてドットを使用して数値を入力する必要があります (例: 0.50)。