Python で指数分布を使用する方法
指数分布は、特定のイベントが発生するまで待機する時間をモデル化するために使用される確率分布です。
確率変数X が指数分布に従う場合、 Xの累積分布関数は次のように書くことができます。
F (x; λ) = 1 – e -λx
金:
- λ:速度パラメータ (λ = 1/μ として計算)
- e: 2.718 にほぼ等しい定数
このチュートリアルでは、Python で指数分布を使用する方法を説明します。
指数分布を生成する方法
Python の SciPy ライブラリのexpon.rvs(scale, size)関数を使用して、特定のレート パラメーターとサンプル サイズで指数分布からランダムな値を生成できます。
from scipy. stats import expo #generate random values from exponential distribution with rate=40 and sample size=10 expon. rvs (scale= 40 , size= 10 ) array([116.5368323 , 67.23514699, 12.00399043, 40.74580584, 34.60922432, 2.68266663, 22.70459831, 97.66661811, 6.64272914, 46.15547298])
注: SciPy ライブラリの完全なドキュメントはここで見つけることができます。
指数分布を使用して確率を計算する方法
特定の間欠泉の噴火間の平均分数が 40 分であると仮定します。噴火までに 50 分未満で待機する必要がある可能性はどのくらいですか?
この問題を解決するには、まずレート パラメーターを計算する必要があります。
- λ = 1/μ
- λ = 1/40
- λ = 0.025
λ = 0.025 と x = 50 を CDF 式に代入できます。
- P(X ≤ x) = 1 – e -λx
- P(X ≤ 50) = 1 – e -0.025(50)
- P(X ≤ 50) = 0.7135
次の噴火までに 50 分未満待たなければならない確率は0.7135です。
SciPy のexpon.cdf()関数を使用して、Python でこの問題を解決できます。
from scipy. stats import expo #calculate probability that x is less than 50 when mean rate is 40 expon. cdf (x=50, scale=40) 0.7134952031398099
次の噴火までに 50 分未満待たなければならない確率は0.7135です。
これは手動で計算した値に対応します。
指数分布をプロットする方法
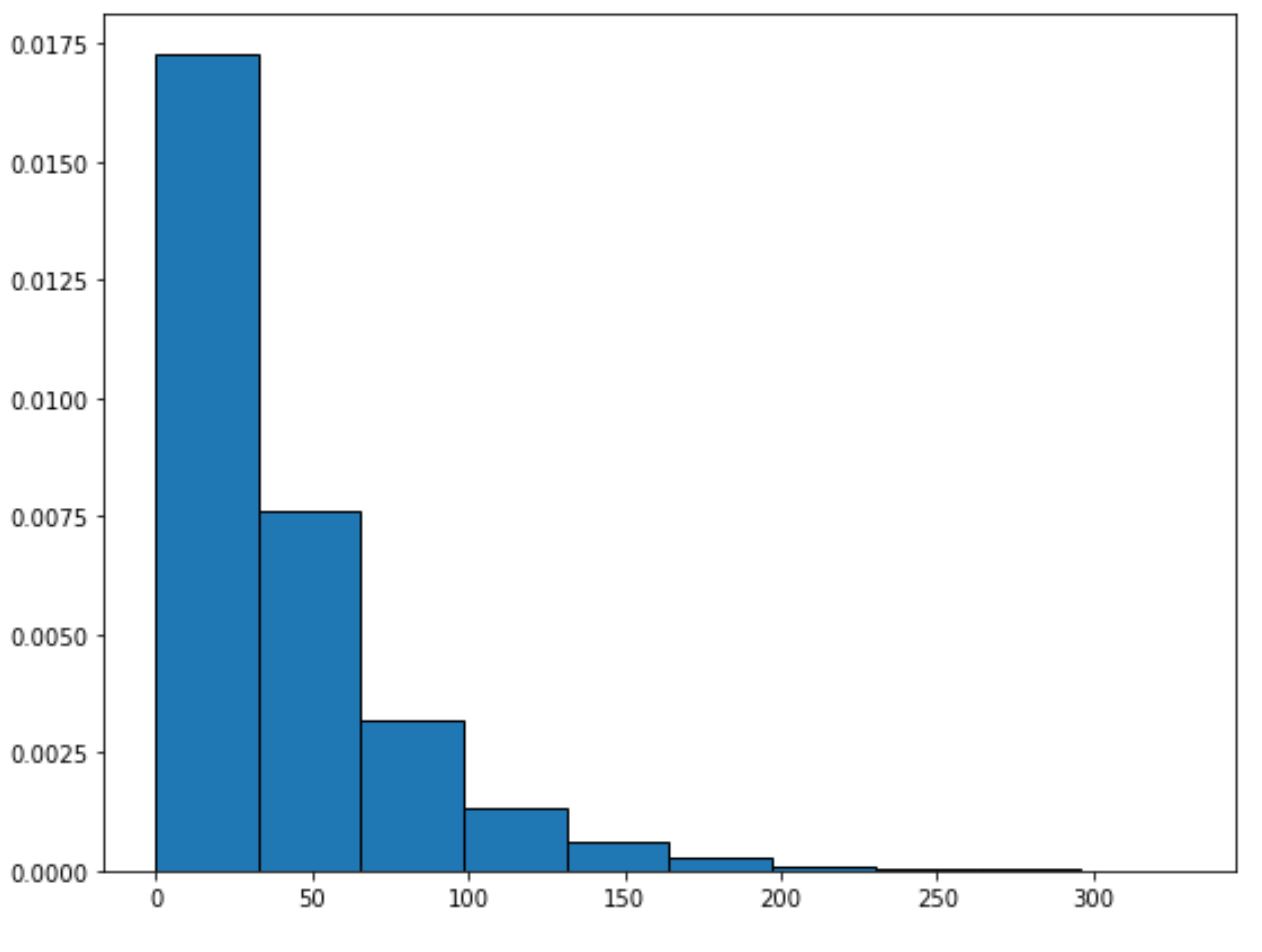
次の構文を使用して、指定されたレート パラメーターで指数分布をプロットできます。
from scipy. stats import expo import matplotlib. pyplot as plt #generate exponential distribution with sample size 10000 x = expon. rvs (scale= 40 ,size= 10000 ) #create plot of exponential distribution plt. hist (x, density= True , edgecolor=' black ')
追加リソース
次のチュートリアルでは、Python で他の一般的なディストリビューションを使用する方法を説明します。
Python でポアソン分布を使用する方法
Python で t 分布を使用する方法
Python で一様分布を使用する方法