教育における統計の重要性 (例付き)

によるベンジャミン・アンダーソン博士 7月 19, 2023 ガイド 0コメント

統計の分野は、データの収集、分析、解釈、表示に関係します。

教育の文脈では、次の理由から統計が重要です。

理由 1 : 統計により、教育者は記述統計を使用して生徒の成績を理解できます。

理由 2 : 統計により、教師はデータの視覚化を使用して生徒の成績の傾向を見つけることができます。

理由 3 : 統計により、教育者は仮説検定を使用してさまざまな教育方法を比較できます。

この記事の残りの部分では、これらのそれぞれの理由を説明します。

記述統計はデータを説明するために使用されます。

教育現場では、教師はクラスの生徒について次の記述統計を計算できます。

これらの測定のおかげで、教師はクラスの生徒の特定の試験の結果をよりよく理解できるようになります。

その後、彼女は、試験に合格する生徒が少なすぎる場合に指導方法を変更するか、あるいは試験の結果が悪かった生徒に追加の個別指導の機会を提供するかなどを決定できます。

注: これらのタイプの記述統計は、教育のあらゆるレベルで使用されます。たとえば、校長は記述統計を使用して、学校全体の生徒のテストのスコアを監視できます。州教育省は、記述統計を使用して、州全体の学生のテストのスコアを監視することもあります。

教育で統計を使用するもう 1 つの一般的な方法は、折れ線グラフ、ヒストグラム、箱ひげ図、円グラフ、その他のグラフなどのデータを視覚化することです。

これらの種類のグラフは、教育者が教室のパフォーマンスや個々の生徒のパフォーマンスの傾向を特定するのに役立つためによく使用されます。

たとえば、教師が次の棒グラフを作成して、年間を通しての試験の平均点を視覚化するとします。

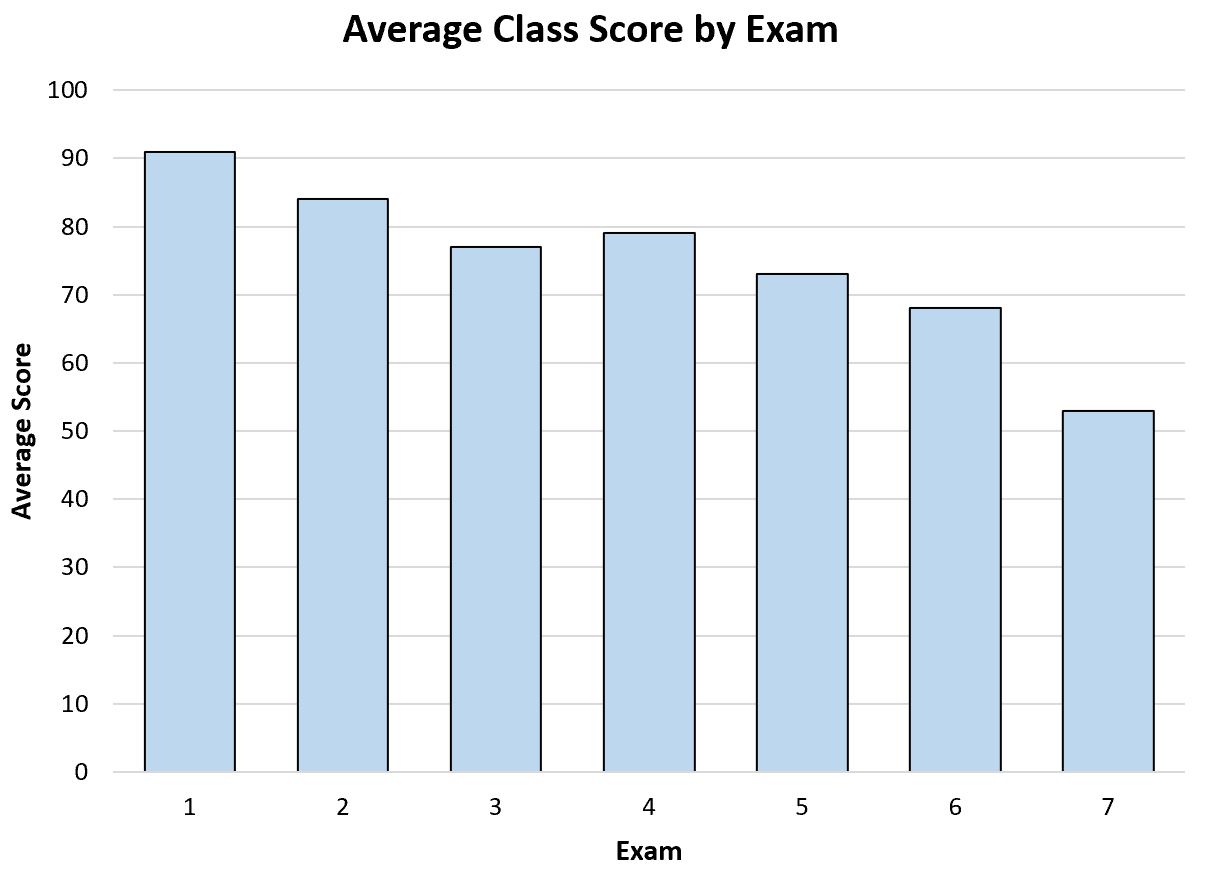
この棒グラフを見るだけで、教師はクラスの生徒のテストの平均点が年間を通じて徐々に低下していることがわかります。

これにより、教師は指導方法を改善したり、生徒にアンケートを実施して指導方法などについて意見を求めることができます。

統計は教育でも仮説検証の形で使用されます。

これらは、教育者が異なる教育方法間に統計的有意性があるかどうかを判断するために使用できるテストです。

たとえば、教師が特定のカリキュラムがテストの得点に影響するかどうかを判断したいとします。これをテストするために、彼は 15 人の学生をランダムに選択して事前テストを受けさせます。次に、各生徒にそのカリキュラムを 1 か月間受講させ、その後、同様の難易度の事後テストを受けさせます。

15 人の生徒それぞれのテスト結果は次のとおりです。

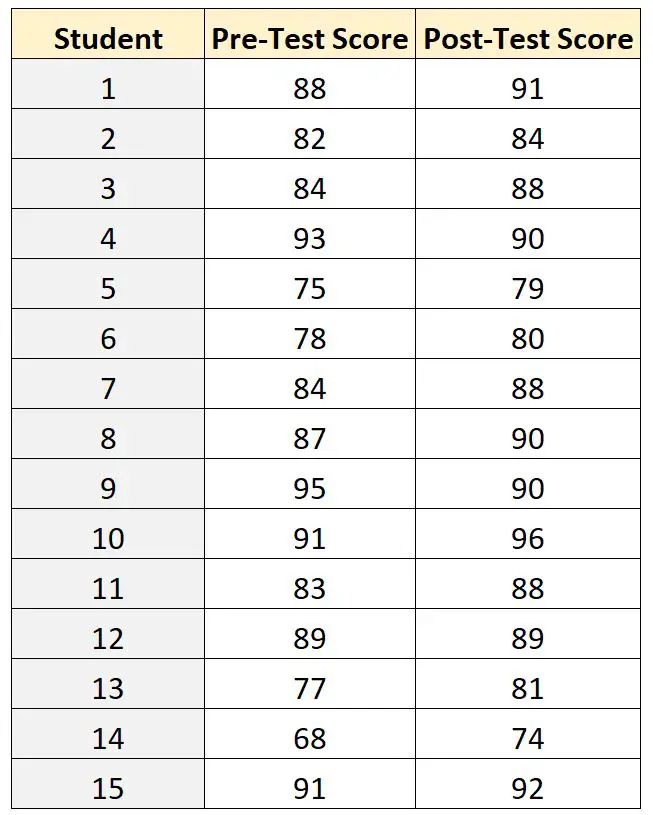
各生徒のテスト前のスコアをテスト後のスコアと関連付けることができるため、教師はテスト前とテスト後の平均スコアの差を比較するために、一対の t テストサンプルを使用できます。

教授が統計ソフトウェアを使用してこの対応サンプル t 検定を実行し、次の結果を受け取ったとします。

この例では、対応のあるサンプルの t 検定で次の帰無仮説と対立仮説が使用されます。

p 値 ( 0.0101 ) は 0.05 未満であるため、帰無仮説を棄却します。

これは、学習プログラムに参加する前と後の生徒のテストの平均点が異なると言える十分な証拠があることを意味します。

注: これは教育で使用される仮説検証の一例にすぎません。その他の一般的な検定には、 1 サンプル t 検定、 2 サンプル t 検定、一元配置分散分析、二元配置分散分析などがあります。

次の記事では、他の分野における統計の重要性について説明しています。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る