下の四角
この記事では、統計における最小二乗とは何か、最小二乗法とは何か、最小二乗基準によって回帰モデルがどのように適合されるかについて説明します。
最小二乗法とは何ですか?
最小二乗法は、回帰式を決定するために使用される統計的手法です。言い換えれば、最小二乗法は、回帰式を計算するときに得られる誤差を最小限に抑えるために回帰モデルで使用される基準です。
具体的には、最小二乗法は残差の二乗和を最小化することで構成されます。つまり、回帰モデルによって予測された値と観測値との差の二乗和を最小化することに基づいています。 。 。以下では、回帰モデルが最小二乗基準によってどのように適合されるかを詳しく見ていきます。
最小二乗法の主な特徴は、観測値と回帰関数の間の最長距離が最小化されることです。他の回帰基準とは異なり、最小二乗法では、大きな数の二乗は小さな数の二乗よりもはるかに大きいため、小さな残差よりも大きな残差を最小化することがより重要であると考えられます。番号。
推定誤差
最小二乗法の概念を完全に理解するには、まず回帰モデルの残差について明確にする必要があります。したがって、推定誤差とは何か、またその計算方法については以下で説明します。
統計学では、推定誤差 は残差とも呼ばれ、真の値と回帰モデルによって近似された値との差です。したがって、統計的残差は次のように計算されます。
![]()
金:
-

はデータ i の残差です。
-

はデータ i の実数値です。
-

は、データ i の回帰モデルによって提供される値です。
したがって、データの残差が大きくなるほど、回帰モデルがこのデータにうまく適応できなくなります。したがって、残差が小さいほど、実際の値と予測値の間の距離は小さくなります。
同様に、データの残差が正の場合、回帰モデルが真の値よりも低い値を予測していることを意味します。一方、残差が負の場合、予測値が実際の値よりも大きいことを意味します。
誤差二乗を最小限に抑える
統計における残差が何であるかを理解したので、誤差二乗がどのように最小化されるかを理解するのが簡単になります。
誤差の 2 乗は残差の 2 乗であるため、誤差の 2 乗は、真の値と回帰モデルによって適合された値の 2 乗の差に等しくなります。
![]()
金:
-
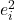
はデータ i の残差の 2 乗です。
-

はデータ i の実数値です。
-

は、データ i の回帰モデルによって提供される値です。
したがって、最小二乗法は、誤差の二乗和を最小化することによって回帰モデルを作成することから構成されます。したがって、最小二乗基準は次の式の最小化に基づいています。
![Rendered by QuickLaTeX.com \begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0a82d4d723b77093b4d584609f372cd7_l3.png)
これが、最小二乗基準が最小二乗基準とも呼ばれる理由です。
前の式でわかるように、最小二乗基準では、小さな残差よりも大きな残差を最小化することに重点が置かれます。たとえば、1 つの剰余が 3 で、別の剰余が 5 の場合、それらの二乗はそれぞれ 9 と 25 であるため、最小二乗基準では最初の剰余よりも前に 2 番目の剰余の最小化が優先されます。
最小二乗調整
最小二乗基準を使用した回帰モデルのフィッティングは、残差の二乗を最小化する回帰モデルを見つけることから構成されます。したがって、回帰モデルから得られる方程式は、観測値と近似値の差の二乗が最小となる方程式となります。
次の例では、回帰モデルを作成するための基準がさらにあり、選択した基準に応じて回帰式が異なることに注意してください。
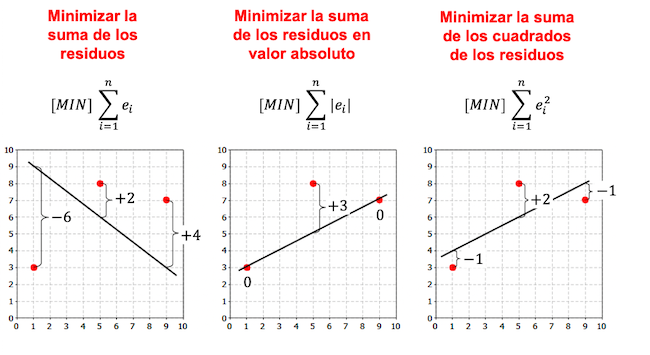
前の例でわかるように、同じデータセットの線形回帰モデルから得られる直線は、選択した基準によって異なります。一般に、回帰モデルでは最小二乗基準が使用されます。
統計学で最も広く使用されている回帰モデルは、独立変数 X と従属変数 Y の関係を直線で近似する単純線形回帰モデルです。
![]()
したがって、データセットを単純な線形回帰モデルに当てはめる式は次のとおりです。

![]()
次のリンクをクリックすると、最小二乗基準を使用して単純な線形回帰モデルが計算される方法の例を確認できます。