X^3の期待値の計算方法

X で示される確率変数の場合、次の式を使用して X ³の期待値を計算できます。

E(X ³ ) = Σx ³ * p(x)

金：

• Σ ：「和」を意味する記号
• x : 確率変数の値
• p(x) : 確率変数が指定された値を取る確率

次の例は、この公式を実際に使用する方法を示しています。

例: X ³の期待値の計算

確率変数が次の確率に達する確率を説明する次の確率分布表があるとします。

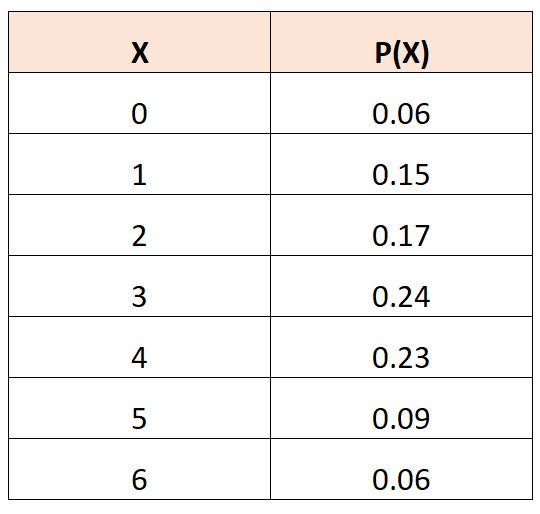
X ³の期待値を計算するには、次の式を使用できます。

E(X ³ ) = Σx ³ * p(x)

E(X ³ ) = (0) ³ *.06 + (1) ³ *.15 + (2) ³ *.17 + (3) ³ *.24 + (4) ³ *.23 + (5) ³ *.09 + (6) ³ *.06

E(X ³ ) = 0 + 0.15 + 0.1.36 + 6.48 + 14.72 + 11.25 + 12.96

E(X ³ ) = 45.596

X ³の期待値は45,596です。

この確率変数は離散確率変数であることに注意してください。つまり、有限数の値のみを取ることができます。

X が連続確率変数の場合、次の式を使用して X ³の期待値を計算する必要があります。

E(X ³ ) = ∫ x ³ f(x)dx

金：

• ∫：「統合」を意味する記号
• f(x) : 確率変数に対して確率密度関数が継続されます。

の期待値^を計算すると、

追加リソース

次のチュートリアルでは、統計におけるその他の一般的なタスクを実行する方法について説明します。

確率分布の平均を求める方法
確率分布の標準偏差を見つける方法
確率分布の分散を求める方法