標本分布とは何ですか?

10,000 頭のイルカの個体群があり、その個体群におけるイルカの平均体重が 300 ポンドであると想像してください。

この母集団から 50 頭のイルカの単純なランダム サンプルを抽出すると、このサンプルのイルカの平均体重が 305 ポンドであることがわかります。

次に、50 頭のイルカからなる別の単純なランダム サンプルを取得すると、このサンプルのイルカの平均体重が 295 ポンドであることがわかります。

50 頭のイルカの単純な無作為サンプルを採取する場合、サンプル内のイルカの平均体重は母集団平均の 300 ポンドに近い可能性がありますが、正確に 300 ポンドではありません。

この母集団から 50 頭のイルカの単純なランダム サンプルを 200 個取得し、各サンプルの平均体重のヒストグラムを作成すると想像してみましょう。

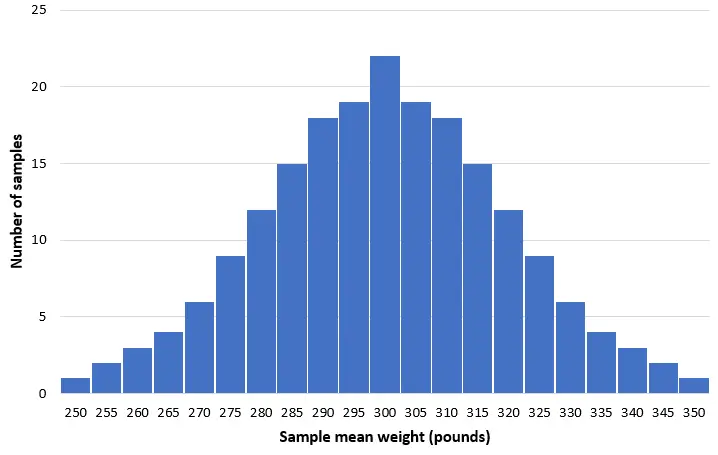
ほとんどのサンプルでは、平均重量は 300 ポンド近くになります。まれに、平均体重がわずか 250 ポンドの小さなイルカがいっぱいサンプルとして採取されることがあります。あるいは、平均体重 350 ポンドのハンドウイルカをいっぱいサンプルとして採取するかもしれません。一般に、標本平均の分布はほぼ正規分布となり、分布の中心は母集団の真の中心に位置します。

この標本平均値の分布は平均値の標本分布と呼ばれ、次の特性があります。

_μx = μ

ここで、μ _xは標本平均、μ は母集団平均です。

_σx = σ/√n

ここで、σ _xは標本標準偏差、σ は母集団標準偏差、n は標本サイズです。

たとえば、このイルカの集団では、平均体重が μ = 300 であることがわかっています。したがって、標本分布の平均はμ _x = 300となります。

母集団の標準偏差が 18 ポンドであることもわかっているとします。したがって、標本の標準偏差はσ _x = 18/ √50 = 2.546となります。

割合の標本分布

同じ 10,000 頭のイルカの個体数を考えてみましょう。イルカの 10% が黒く、残りが灰色であると仮定します。 50 頭のイルカから単純に無作為にサンプルを採取し、そのサンプル中のイルカの 14% が黒人であることが判明したとします。次に、50 頭のイルカから別の単純なランダム サンプルを取得すると、このサンプルのイルカの 8% が黒であることがわかります。

この母集団から 50 頭のイルカの単純なランダム サンプルを 200 個取得し、各サンプルにおける黒いイルカの割合のヒストグラムを作成すると想像してください。

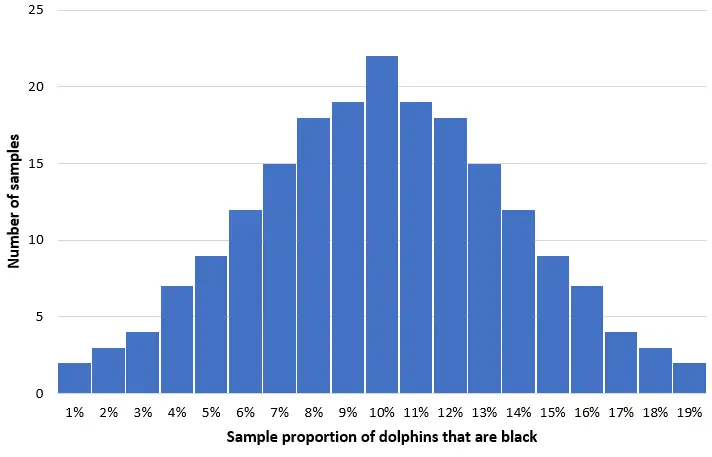
ほとんどのサンプルでは、黒いイルカの割合は実際の個体数の 10% に近くなります。黒いイルカのサンプル割合の分布はほぼ正規になり、分布の中心は個体群の真の中心に位置します。

この標本比率の分布は比率の標本分布として知られており、次の特性があります。

_μp = P

ここで、 pはサンプルの割合、 Pは母集団の割合です。

σ _p = √ (P)(1-P) / n

ここで、P は母集団の割合、n はサンプルサイズです。

たとえば、このイルカの個体群では、黒いイルカの真の割合は 10% = 0.1 であることがわかります。したがって、比例サンプリング分布の平均はμ _p = 0.1です。

母集団の標準偏差が 18 ポンドであることもわかっているとします。したがって、標本標準偏差はσ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042となります。

正常性を確立する

上の式を使用するには、標本分布が正規分布である必要があります。

中心極限定理によれば、たとえ母集団の分布が正規でなくても、サンプルサイズが十分に大きければ、標本平均の標本分布はほぼ正規になります。ほとんどの場合、サンプル サイズは 30 以上あれば十分であると考えられます。

期待される成功数と失敗数が両方とも 10 以上であれば、標本比率の標本分布はほぼ正規になります。

例

標本分布を使用して確率を計算できます。

例 1:特定のマシンが Cookie を作成します。これらのクッキーの重量分布は右に偏っており、平均は 10 オンス、標準偏差は 2 オンスです。この機械で製造された 100 個のクッキーの単純なランダム サンプルを取得した場合、このサンプル内のクッキーの平均重量が 9.8 オンス未満である確率はどれくらいですか?

ステップ 1: 正常性を確立する。

標本平均値の標本分布が正規分布であることを確認する必要があります。中心極限定理に従って標本サイズが 30 以上であるため、標本平均の標本分布は正規であると仮定できます。

ステップ 2: 標本分布の平均値と標準偏差を求めます。

_μx = μ

_σx = σ/√n

μ _x = 10オンス

σ _x = 2/√100 = 2/10 = 0.2オンス

ステップ 3: Z スコア面積計算ツールを使用して、このサンプルのクッキーの平均重量が 9.8 オンス未満である確率を決定します。

Z スコア領域計算ツールに次の数値を入力します。この例では数値が 1 つしか見つからないため、「Raw Score 2」は空白のままにしておきます。

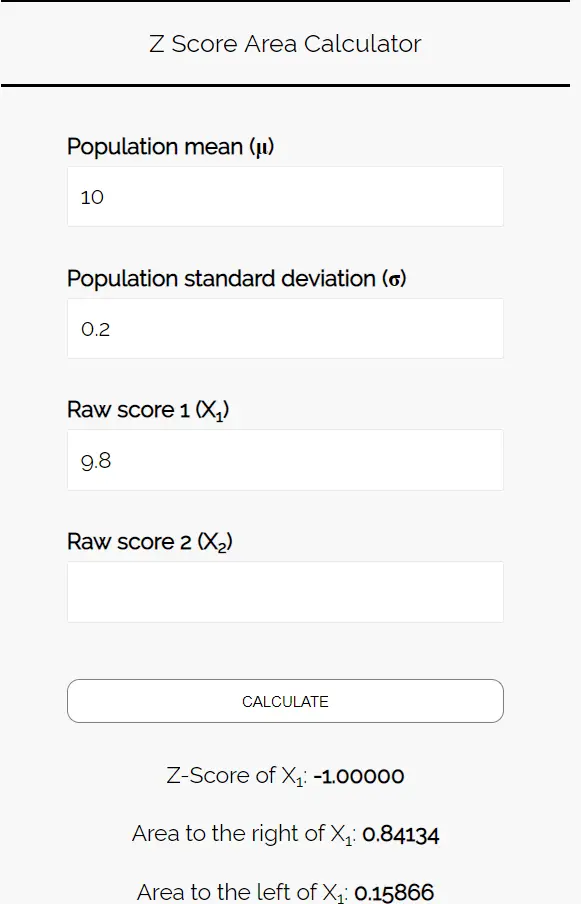
このサンプルのクッキーの平均重量が 9.8 オンス未満である確率を知りたいので、9.8 の左側の領域に注目します。計算機は、この確率が0.15866であることを示します。

例 2:全校調査によると、特定の学校の生徒の 87% はアイスクリームよりもピザを好みます。 200 人の学生から単純に無作為にサンプルを抽出したとします。ピザを好む学生の割合が 85% 未満である確率はどれくらいですか?

ステップ 1: 正常性を確立する。

予想される「成功」と「失敗」の数が両方とも 10 以上であれば、標本比率の標本分布はほぼ正規分布になることを思い出してください。

この場合、ピザを好むと予想される生徒の数は、87% * 200 人の生徒 = 174 人の生徒になります。ピザを好まないと予想される生徒の数は、13% * 200 人の生徒 = 26 人の生徒です。これらの数値はどちらも少なくとも 10 であるため、ピザを好む生徒の割合の標本分布はほぼ正規であると仮定できます。

ステップ 2: 標本分布の平均値と標準偏差を求めます。

_μp = P

σ _p = √ (P)(1-P) / n

_μp = 0.87

σ _p = √ (0.87)(1-0.87) / 200 = 0.024

ステップ 3: Z スコア面積計算ツールを使用して、ピザを好む生徒の割合が 85% 未満である確率を決定します。

Z スコア領域計算ツールに次の数値を入力します。この例では数値が 1 つしか見つからないため、「Raw Score 2」は空白のままにしておきます。

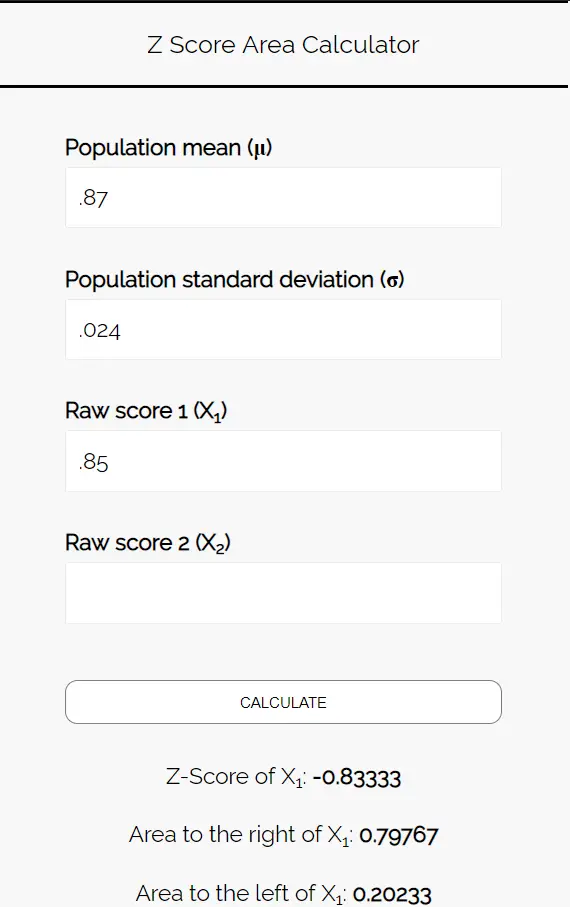
ピザを好む学生の割合が 85% 未満である確率を知りたいため、0.85 の左側の領域に注目します。計算機は、この確率が0.20233であることを示します。