標本分布

によるベンジャミン・アンダーソン博士 8月 3, 2023 統計 0コメント

この記事では、統計における標本分布とは何か、またそれが何に使用されるのかについて説明します。ここでは、標本分布の意味、標本分布の具体例、さらに最も一般的なタイプの標本分布の式について説明します。

標本分布とは何ですか?

標本分布、または標本分布は、母集団から考えられるすべての標本を考慮した結果として得られる分布です。つまり、標本分布は、母集団から考えられるすべての標本の標本パラメータを計算して得られる分布です。

たとえば、統計母集団から考えられるすべてのサンプルを抽出し、各サンプルの平均を計算すると、サンプル平均のセットが標本分布を形成します。より正確には、計算されたパラメータは算術平均であるため、平均値の標本分布になります。

統計学では、標本分布は、単一の標本を調査するときに母集団パラメータの値に近づく確率を計算するために使用されます。同様に、標本分布により、特定のサンプルサイズの標本誤差を推定することができます。

サンプリング分布の例

標本分布の定義がわかったので、概念を完全に理解するために簡単な例を見てみましょう。

箱の中に 3 つのボールを置き、それぞれに 1 から 3 までの番号が書かれています。つまり、1 つのボールには 1、もう 1 つのボールには 2、最後のボールには 3 が付けられます。サイズ n = のサンプルの場合、 2、置換を含むサンプルが選択された場合の平均のサンプル分布の確率を計算します。

サンプルは置換によって選択されます。つまり、サンプルの最初の要素を選択するために拾ったボールはボックスに戻され、2 回目の抽出中に再度選択できます。したがって、母集団から抽出できるすべてのサンプルは次のようになります。

1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3

したがって、考えられる各サンプルの算術平均を計算します。

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

したがって、母集団から無作為にサンプルを選択した場合に、サンプル平均の各値が得られる確率は次のようになります。

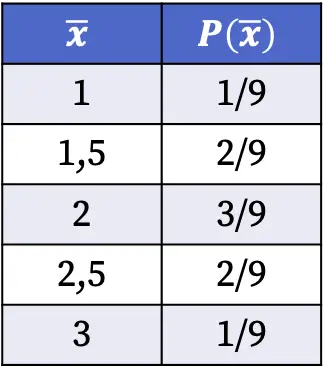
上の表に示されているサンプル分布の確率は、上記の平均値を持つサンプルの数を可能なケースの総数で割ることによって計算されました。たとえば、サンプル平均は 9 つのケースのうち 2 つのケースで 1.5 であるため、P(1.5)=2/9 になります。

標本分布の種類

標本分布 (または標本分布) は、それを取得した標本パラメータに基づいて分類できます。したがって、最も一般的なディストリビューションの種類は次のとおりです。

平均の標本分布: これは、各サンプルの算術平均を計算した結果得られる標本分布です。
割合標本分布：全サンプルの割合を計算して得られる標本分布です。
分散の標本分布: これは、標本内のすべての分散のセットを形成する標本分布です。
平均値の差の標本分布: 2 つの異なる母集団から得られるすべての標本の平均値の差を計算して得られる標本分布です。
比率の差標本分布: 2 つの母集団から考えられるすべての標本比率を差し引くことによって得られる標本分布です。

それぞれのタイプの標本分布については、以下でさらに詳しく説明します。

平均値の標本分布

平均値が正規確率分布に従う母集団を仮定すると、

$\mu$

と標準偏差

$\sigma$

サイズサンプルが抽出されます

$n$

の場合、平均値の標本分布は次の特性を持つ正規分布によって定義されることになります。

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

金

$\mu_{\overline{x}}$

は平均値の標本分布の平均値であり、

$\sigma_{\overline{x}}$

はその標準偏差です。さらに、

$\cfrac{\sigma}{\sqrt{n}}$

は標本分布の標準誤差です。

注:母集団が正規分布に従わないが、サンプルサイズが大きい (n>30) 場合、平均値の標本分布は中心定理の制限によって上記の正規分布に近似することもできます。

したがって、平均値の標本分布は正規分布に従うため、標本平均値に関連する確率を計算する式は次のようになります。

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

金：

$\overline{x}$

はサンプル平均です。
$\mu$

これは母集団の平均です。
$s$

は母集団の標準偏差です。
$n$

はサンプルサイズです。
$Z$

は、標準正規分布 N(0,1) によって定義される変数です。

➤参照:平均値の標本分布に関する解決済み演習

割合の標本分布

実際、サンプルの一部を調査するときは、成功事例を分析します。したがって、研究の確率変数は二項確率分布に従います。

中心極限定理によれば、大きなサイズ (n>30) の場合、二項分布を正規分布に近づけることができます。したがって、比率の標本分布は、次のパラメーターを使用して正規分布に近似します。

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

金

$p$

は成功の確率であり、

$q$

失敗の確率です

$q=1-p$

。

注:二項分布は、次の場合にのみ正規分布に近似できます。

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> 、</p> <p class=$ $np\ge 5$

そして

$nq\ge 5$

。

したがって、割合の標本分布は正規分布に近似できるため、標本の割合に関連する確率を計算する式は次のようになります。

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

金：

$\widehat{p}$

はサンプルの割合です。
$p$

人口に占める割合です。
$q$

は母集団が失敗する確率であり、

$q=1-p$

。
$n$

はサンプルサイズです。
$Z$

は、標準正規分布 N(0,1) によって定義される変数です。

➤参照:比率の標本分布に関する解決済み演習

標本分散分布

分散の標本分布は、カイ二乗確率分布によって定義されます。したがって、標本分散分布の統計量の式は次のようになります。

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

金：

$\chi^2$

は、カイ二乗分布に従う標本分散分布の統計量です。
$n$

はサンプルサイズです。
$s^2$

は標本分散です。
$\sigma^2$

は母集団分散です。

➤参照:分散の標本分布に関する解決済み演習

平均値の差の標本分布

サンプルサイズが十分に大きい場合 (n ₁ ≥30 および n ₂ ≥30)、平均差のサンプル分布は正規分布に従います。より正確には、前記分布のパラメータは次のように計算されます。

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

注:両方の母集団が正規分布である場合、サンプルサイズに関係なく、平均の差の標本分布は正規分布に従います。

したがって、平均値の差の標本分布は正規分布で定義されるため、平均値の差の標本分布の統計量を計算する式は次のようになります。

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

金：

$\overline{x_i}$

はサンプル i の平均です。
$\mu_i$

は母集団 i の平均です。
$\sigma_i$

は母集団 i の標準偏差です。
$n_i$

はサンプルサイズ i です。
$Z$

は、標準正規分布 N(0,1) によって定義される変数です。

異なる母集団からのサンプルは異なるサンプルサイズを持つ可能性があることに注意してください。

➤参照:平均値の差の標本分布に関する解決済み演習

比率の差の標本分布

実際の目的では、比率は観測値の総数に対する成功事例の比率であるため、比率の違いのサンプリング分布のために選択されたサンプルは二項分布によって定義されます。

ただし、中心極限定理により、二項分布は正規確率分布に近似できます。したがって、比率の差の標本分布は、次の特性を持つ正規分布に近似できます。

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$