標準化と正規化: 違いは何ですか?

標準化と正規化は、データのサイズを変更する 2 つの方法です。

正規化では、平均が 0、標準偏差が 1 になるようにデータ セットをスケーリングします。これを行うには、次の式を使用します。

x_新しい= (x _i – x ) / s

金：

• x _i : データセットの^{i 番目の}値
• x : サンプルの意味
• s : サンプルの標準偏差

正規化では、各値が 0 から 1 の間になるようにデータ セットのサイズが変更されます。これは、次の式を使用して行われます。

x_新しい= (x _i – x_最小) / (x_最大– x_最小)

金：

• x _i : データセットの^{i 番目の}値
• x _min : データセット内の最小値
• x _max : データセット内の最大値

次の例は、実際にデータセットを標準化および正規化する方法を示しています。

例: データを標準化する方法

次のデータセットがあるとします。

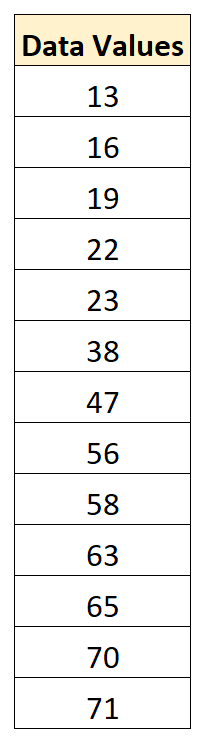
データセットの平均値は 43.15 で、標準偏差は 22.13 です。

最初の値13 を正規化するには、以前に共有した式を適用します。

• x_新しい= (x _i – x ) / s = (13 – 43.15) / 22.13 = -1.36

2 番目の値16 を正規化するには、同じ式を使用します。

• x_新しい= (x _i – x ) / s = (16 – 43.15) / 22.13 = -1.23

3 番目の値19 を正規化するには、同じ式を使用します。

• x_新しい= (x _i – x ) / s = (19 – 43.15) / 22.13 = -1.09

これとまったく同じ式を使用して、元のデータセットの各値を標準化できます。

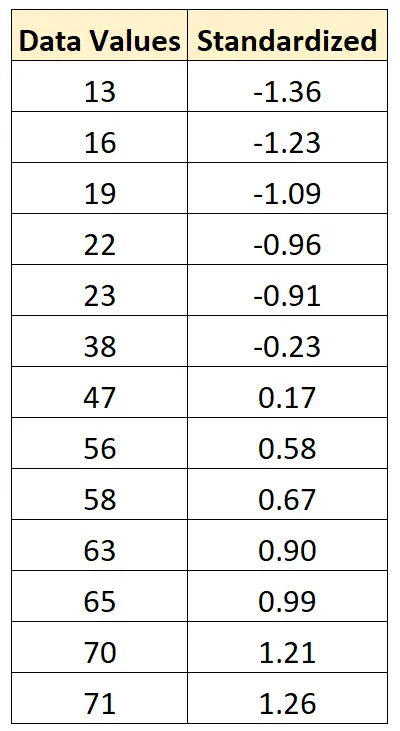
例: データを正規化する方法

もう一度、次のデータセットがあると仮定します。

データセットの最小値は 13 で、最大値は 71 です。

最初の値13 を正規化するには、以前に共有した式を適用します。

• x_新しい= (x _i – x _min ) / (x _max – x _min ) = (13 – 13) / (71 – 13) = 0

2 番目の値16 を正規化するには、同じ式を使用します。

• x_新しい= (x _i – x _min ) / (x _max – x _min ) = (16 – 13) / (71 – 13) = 0.0517

3 番目の値19 を正規化するには、同じ式を使用します。

• x_新しい= (x _i – x _min ) / (x _max – x _min ) = (19 – 13) / (71 – 13) = 0.1034

これとまったく同じ式を使用して、元のデータセットの各値を 0 と 1 の間で正規化できます。

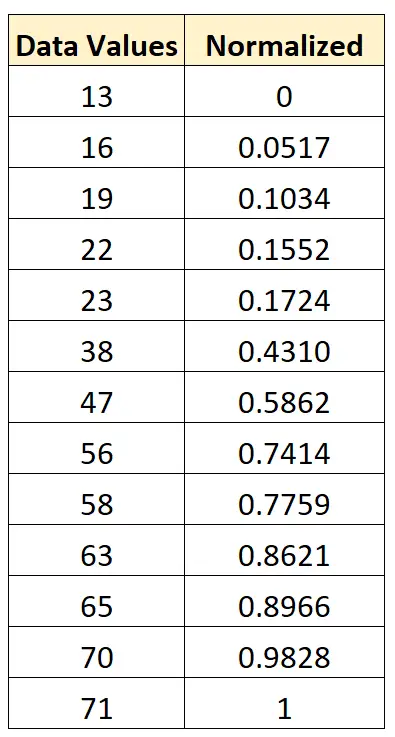
標準化または正規化: いつ使用するか?

通常、複数の変数を異なるスケールで測定し、各変数の範囲を同じにするような、ある種の分析を行うときにデータを正規化します。

これにより、特に変数が異なる単位で測定される場合 (つまり、ある変数がインチで測定され、別の変数がヤードで測定される場合)、1 つの変数が不当な影響を与えることが防止されます。

一方、データセット内の各値が平均からどれだけ標準偏差があるかを知りたい場合は、通常、データを正規化します。

たとえば、特定の学校の 500 人の生徒の試験のスコアのリストがあり、各試験のスコアが平均スコアからどれだけの標準偏差があるかを知りたいとします。

この場合、生データを正規化してこの情報を知ることができます。次に、標準化スコア 1.26 は、この特定の生徒の試験スコアが平均試験スコアより 1.26 標準偏差高いことを示します。

データを正規化するか標準化するかにかかわらず、次の点に留意してください。

• 正規化されたデータセットは常に 0 と 1 の間の値を持ちます。
• 標準化されたデータセットの平均は 0、標準偏差は 1 になりますが、最大値と最小値には特定の上限または下限がありません。

特定のシナリオによっては、データを正規化または標準化する方が合理的である場合があります。

追加リソース

次のチュートリアルでは、さまざまな統計ソフトウェアでデータを標準化および正規化する方法について説明します。

R でデータを正規化する方法
Excel でデータを正規化する方法
Python でデータを正規化する方法
R でデータを標準化する方法