樹形図
この記事では、樹形図とは何か、またその作成方法について説明します。したがって、ツリー構造の例、このタイプの図の利点、さらに段階的に解決される演習が見つかります。
木とは何ですか?
樹形図 は、確率ツリーとも呼ばれ、実験で考えられるすべての結果とその確率をグラフで表現したものです。
したがって、樹状図を使用して、サンプル空間で考えられるすべての結果をグラフ化し、その確率を計算します。
樹形図は、最終結果に到達するまで、各結果 (ノード) が新しい結果 (枝) に分岐するように作成されます。
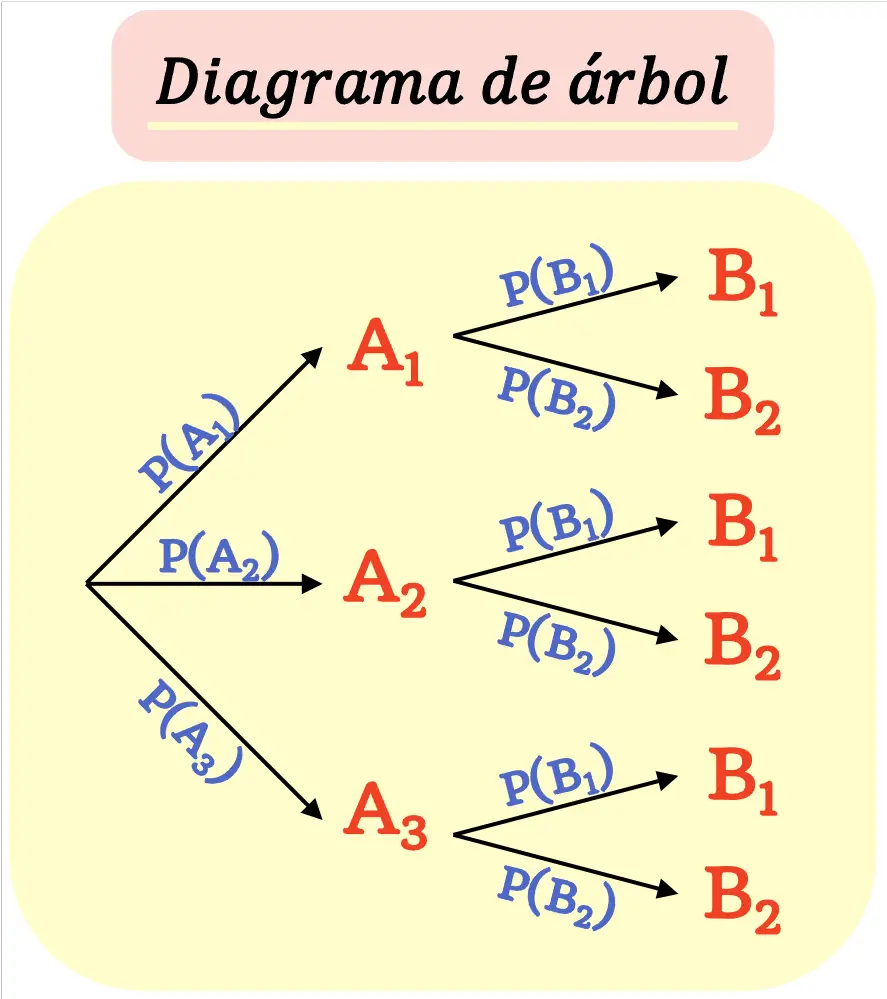
ノードから出るすべての分岐の確率の合計は 1 に等しくなければならないことに留意する必要があります。
樹形図の作り方
ツリーを作成するには、次の手順に従う必要があります。
- 樹形図を作成する最初のステップは、考えられる結果ごとに分岐を描画することです。これらは第 1 世代のブランチになります。
- 次に、各イベントに関連付けられた確率が、対応する分岐に追加されます。
- 各第 1 世代のブランチの終端は、その後に発生する可能性のあるイベントのブランチをそこから表現する必要があるノードです。
- 最初の分岐と同様に、表現されたイベントの確率を追加する必要があります。
- 最終ノード、つまり実験の可能な終了点に到達するまで、ステップ 3 と 4 を繰り返します。
1 つのレベルのブランチの数は、別のレベルのブランチの数と必ずしも同じである必要はないことに注意してください。同様に、考えられる結果から生じる分岐の数は、同じレベル内であっても異なる場合があります。
ツリーの例
樹形図の作成の定義と理論を理解したところで、概念をよりよく理解するために実際の例を段階的に見てみましょう。
- 3 つの独立したコインのコイントスの確率ツリーを構築します。次に、3 回のトスすべてで表になる確率を求めます。
くじを引く場合、考えられる結果は 2 つだけです。表か裏かです。したがって、コインを投げたときに表か裏が出る確率は次のようになります。
![]()
![]()
考えられる結果の確率がわかったら、樹形図の表現に進みます。
コイントスは独立しているため、表または裏が出る確率は、各コインで常に同じになります。したがって、ツリーを構築するには、スローごとに 2 つの枝 (頭と尾) を同じ確率で表現する必要があります。

ツリーを作成したら、あとは 3 枚のコインを投げる確率を判断するだけです。
樹形図の考えられる結果の確率を計算するには、隣接するすべての分岐の確率を乗算する必要があります。
したがって、この場合、表になる確率をすべて乗算する必要があります。これらは、望ましい結果に至る経路の確率であるためです。

したがって、3 回のコイントスで表が出る確率は次のように計算されます。
![]()
つまり、3回連続で表が出る確率は12.5%ということになります。
ツリー演習を解決しました
村には保育園が 3 つしかありません。子供たちの 60% が保育園 A、30% が保育園 B、10% が保育園 C に通っています。さらに、3 つの保育園では、人口の 55% が女の子です。ツリーを構築し、次の確率を計算します。
- 子供がランダムに選択された場合、それが保育園 B の女の子である確率。
- 任意の保育園から子供がランダムに選ばれた場合、その子供が男の子である確率。
すべての保育園における女子の割合が 55% の場合、男子の割合は 1 から 0.55 を引くだけで計算されることに注意してください。
![]()
すべての確率がわかったので、すべての可能性を含む確率ツリーを作成できます。

したがって、保育園 B から女の子をランダムに選択する確率は次のように計算されます。
![]()
一方、保育園で男の子を選択する確率を決定するには、まず各保育園で男の子を選択する確率を見つけて、それらを合計する必要があります。
![]()
![]()
![]()
![]()
ツリー構造のメリット
ツリー構造の特性により、このタイプの統計グラフには次のような利点があります。
- 樹形図は意思決定に非常に役立ちます。
- 考えられるすべての結果間の関係をグラフで表すことができます。
- 問題の根本原因を見つけるのに非常に便利です。
- 確率と統計の問題を解決しやすくなります。
- 樹形図はアイデアを整理し、状況を分析するのに役立ちます。