正の相関
この記事では、統計における正の相関の意味、正の相関を持つ変数の例、他のタイプの相関との違いについて学びます。
正の相関とは何ですか?
統計学における正の相関とは、2 つの異なる変数間の相関の一種です。より具体的には、2 つの変数間の正の相関関係は、一方の変数の値が増加すると、もう一方の変数も増加することを意味します。
2 つの変数間の相関が正であるとみなされるには、相関係数の値が 0 (含まれない) と 1 (両端を含む) の間にある必要があります。
正の相関は直接相関とも呼ばれることに注意してください。
正の相関の例
正の相関の定義を考慮して、そのような相関を示す 2 つの変数の例を以下に示します。
- 次の度数表では、20 人の生徒のサンプルの数学と統計のスコアがデータとして収集されました。 2 つの変数間の関係を分析します。
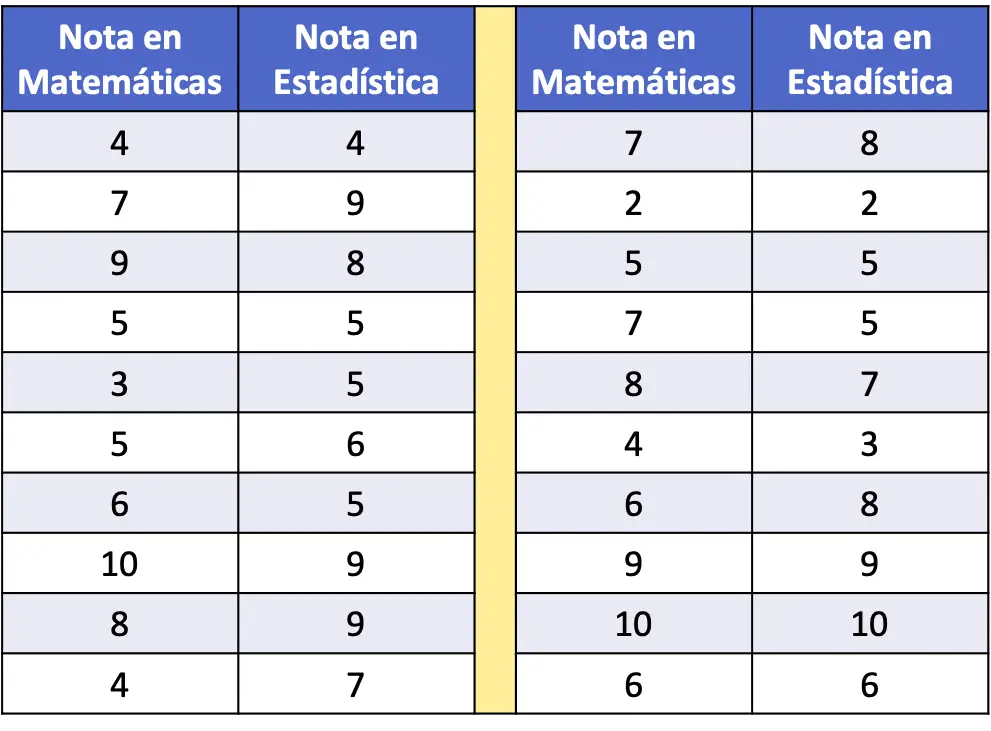
相関係数を計算する前に、まず予備調査のために統計データ セットを散布図で表すことをお勧めします。
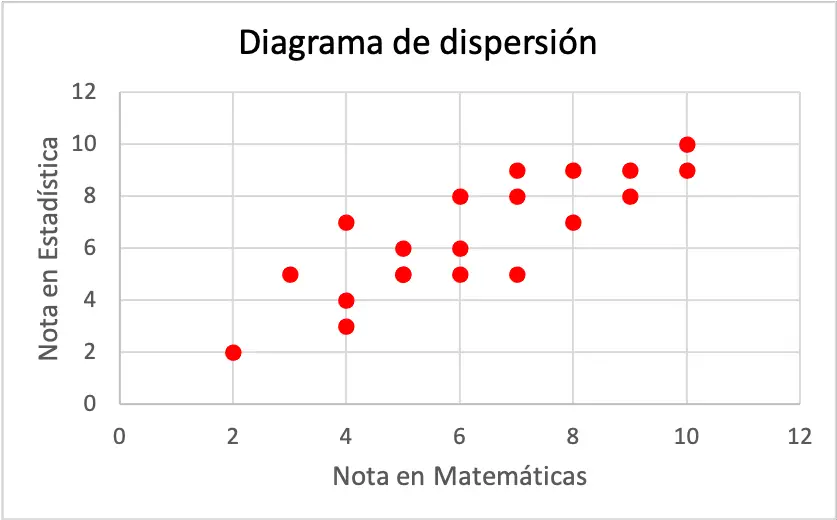
グラフが示すように、数学の成績が上がると統計の成績も上がるため、2 つの変数には正の線形相関があることがわかります。ただし、相関の種類を確実に判断するには、相関係数を計算する必要があります。
![]()
ピアソン相関係数の値は 0 より大きく 1 に非常に近いため、調査した 2 つの変数間の相関関係は確かに正です。
正の相関の解釈
統計における正の相関の意味を理解するために、このセクションでは 2 つの変数間の正の相関の値を解釈する方法を見ていきます。
相関係数の値が高いほど、2 つの変数の正の相関が高くなります。したがって、相関係数の値が 1 に近い場合、2 つの変数間の相関関係が正で非常に強いことを意味します。
一方、相関係数の値が低くゼロに近い場合、2 つの変数間の相関は正であるものの弱いことを意味します。相関係数がゼロまたは負になった場合でも、これは相関がそれぞれゼロまたは負であることを意味します。以下では、これら 3 種類の相関関係の違いを見ていきます。
最後に、正の相関は変数間の因果関係を意味するものではないことに注意してください。つまり、2 つの変数に正の相関がある場合、それらは線形関係にあることを意味しますが、一方の変数が他方の変数の原因であるとは限りません。
前のセクションと同様に、数学と統計の成績には正の相関がありますが、数学で良い成績を取得しても、自動的に統計で良い成績が保証されるわけではなく、両方の科目を勉強する必要があります。結論として、数学の成績は統計の成績の原因ではなく、2 つの変数は単にリンクされているだけです。
正、負、ゼロ相関
統計では、正の相関関係だけでなく、2 つの変数が負の相関関係またはゼロの相関関係を持つこともあります。したがって、このセクションでは、これら 3 つのタイプの相関関係がどのように区別されるかを見ていきます。
- 正の相関: 一方の変数が増加すると、他方の変数も増加します。相関係数の値は 0 (含まれない) と 1 (両端の値を含む) の間です。
- 負の相関: 一方の変数が増加すると他方の変数が減少し、逆も同様で、一方の変数が減少すると他方の変数が増加します。相関係数の値は、-1 (両端を含む) と 0 (両端を含めない) の間です。
- ゼロ相関: 2 つの変数間に関係はありません。相関係数は 0 に等しくなります。
次のグラフでは、各タイプの相関関係が示されています。
