正規分布
この記事では、統計における正規分布とは何かについて説明します。したがって、正規分布の定義、正規分布の例、正規分布の性質がわかります。
正規分布とは何ですか?
正規分布は連続確率分布であり、そのグラフは釣鐘型で平均に対して対称です。統計学では、正規分布は非常に異なる特性を持つ現象をモデル化するために使用されます。そのため、この分布は非常に重要です。
実際、統計学では、正規分布はすべての確率分布の中で最も重要な分布であると考えられています。正規分布は、現実世界の多数の現象をモデル化できるだけでなく、他のタイプの現象を近似するためにも使用できるためです。配布物。特定の条件下で。
正規分布の記号は大文字の N です。したがって、変数が正規分布に従うことを示すために、変数は文字 N で示され、その算術平均と標準偏差の値が括弧内に追加されます。
![]()
正規分布には、ガウス分布、ガウス分布、ラプラス ガウス分布など、さまざまな名前があります。
正規分布の例
通常、正規分布に従うデータセットには多数の観測値が含まれており、非常に一般的なトピックがカバーされています。以下に、一般に正規分布を使用してモデル化できる統計サンプルの例をいくつか示します。
正規分布の例:
- コース内の生徒の規模。
- 会社の従業員のIQ。
- 工場で 1 日に生産される不良部品の数。
- コースの学生が試験で取得した成績。
- 証券取引所に上場されている企業の株式の収益性。
正規分布グラフ
正規分布とは何か、およびこのタイプの確率分布の例をいくつか確認したら、概念をより深く理解するためにそのグラフがどのようなものかを見てみましょう。
次のグラフでは、正規分布の密度関数が算術平均と標準偏差の値に応じてどのように変化するかがわかります。
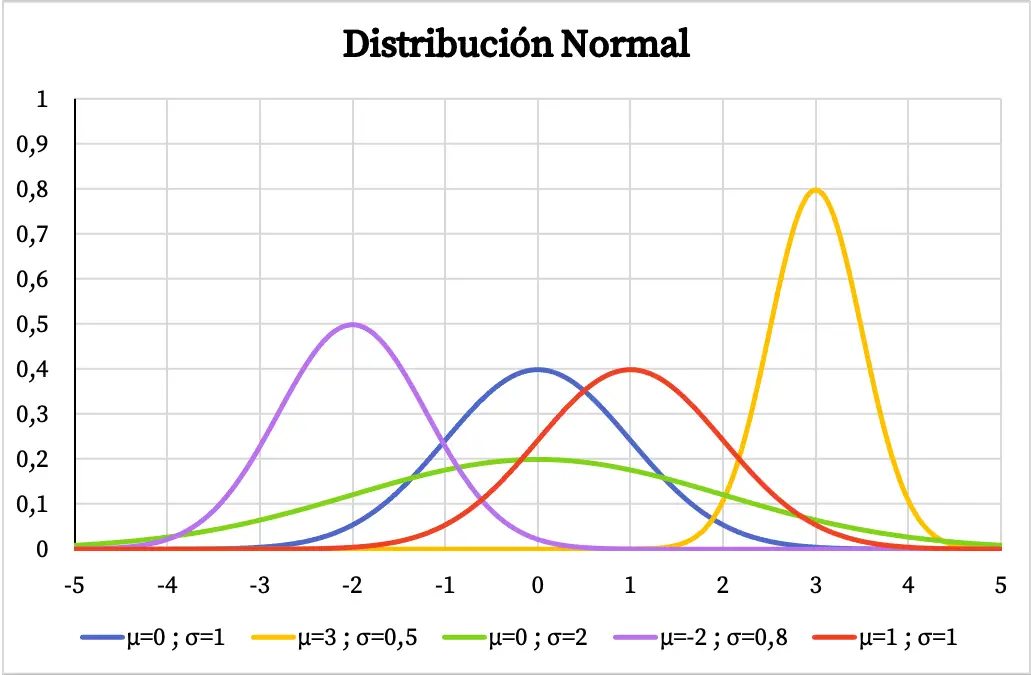
算術平均を中心とした釣鐘型の場合、変数に正規分布がある場合、最も繰り返される値が平均値であり、平均値付近の値が極値よりも頻繁に繰り返されることを意味します。同様に、正規分布の標準偏差が大きいほど、そのグラフ表現の形状は平坦になります。
一方、次の図に示すように、正規分布の累積確率関数のグラフは、その算術平均と標準偏差の値にも依存します。
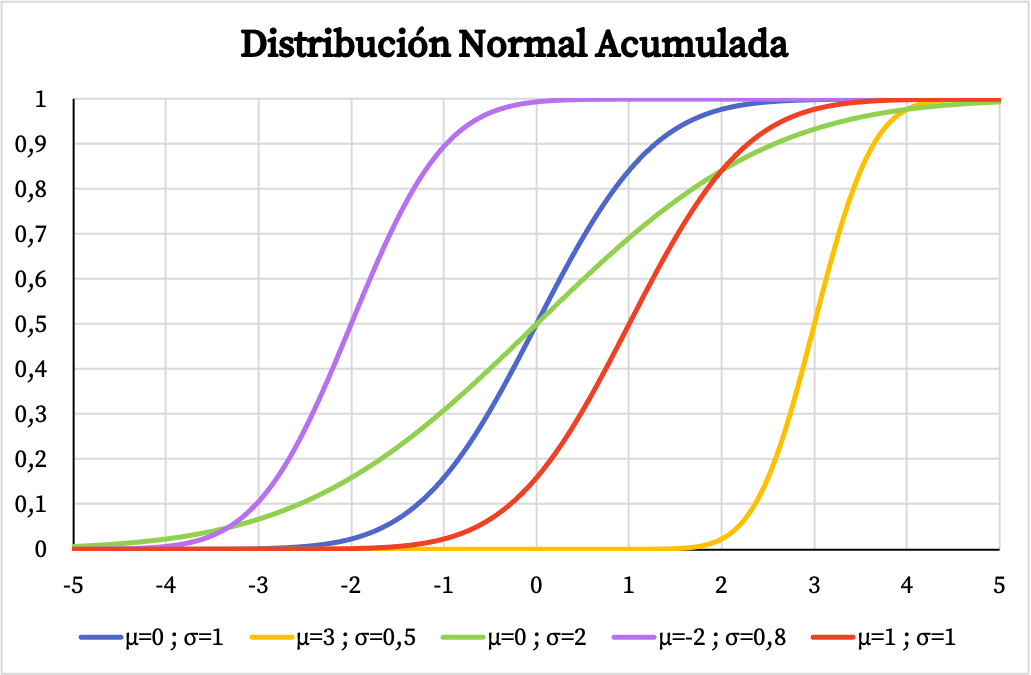
正規分布の密度関数と分布関数を使用すると、この分布に関連付けられた確率を計算できます。ただし、数式を使用する代わりに、正規分布テーブルを直接使用した方が高速なので、正規分布テーブルを直接使用することもできます。次のリンクからこれらの表を参照できます。
正規分布の特徴
正規分布には次のような特徴があります。
- 正規分布は、算術平均 (μ) と標準偏差 (σ) という 2 つの特性パラメータに依存します。
![]()
- 正規分布は正の値も負の値も取ることができるため、正規分布の領域は実数で構成されます。
![]()
- 正規分布の中央値と最頻値は、分布の算術平均に等しくなります。
![]()
- 正規分布の歪度係数と尖度係数はゼロです。
![]()
- 正規分布の密度関数の式は次のとおりです。
![]()
- 同様に、正規分布の累積確率関数の式は次のとおりです。
![]()
- 中心極限定理の応用として、λ の値が十分に大きい場合、ポアソン分布は正規分布に近似できることがわかります。
![]()
- 中心極限定理のもう 1 つの応用は、多数の観測値を持つデータ セットの二項分布を正規分布で近似できることです。
![]()
標準正規分布
標準正規分布 は、単位正規分布とも呼ばれ、正規分布の最も単純なケースです。より正確には、標準正規分布は、平均値と標準偏差値がそれぞれ 0 と 1 に等しい正規分布です。
![Rendered by QuickLaTeX.com \displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ca26cb58ac445099df12aeebda27e38_l3.png)
正規分布は、各値から算術平均を引いて標準偏差で割る、タイピングと呼ばれるプロセスを適用することで標準正規分布に変換できることに注意してください。
さらに、標準正規分布は、その確率テーブルを使用して正規分布の確率を決定するために使用されます。したがって、正規分布の確率を見つけるには、まず変数を入力して標準正規分布に変換し、次にテーブルを調べて対応する確率値が何であるかを確認します。詳細については、次のリンクをクリックしてください。
正規分布と経験則
統計学における経験則は、 68-95-99.7 ルールとも呼ばれ、正規分布内の平均値から 3 標準偏差以内に収まる値の割合を定義するルールです。
より具体的には、経験則では次のことが述べられています。
- 正規分布の値の 68% は、平均値の 1 標準偏差以内にあります。
- 正規分布の値の 95% は、平均値の 2 標準偏差以内にあります。
- 正規分布の値の 99.7% は、平均から 3 標準偏差以内に収まります。
