正規分布と標準正規分布: 違い
正規分布は、統計で最もよく使用される確率分布です。
次のような特性があります。
- 対称
- ベル型
- 平均と中央値は等しいです。どちらも分布の中心に位置します
正規分布の平均はその位置を決定し、標準偏差はその広がりを決定します。
たとえば、次のグラフは、平均と標準偏差が異なる 3 つの正規分布を示しています。
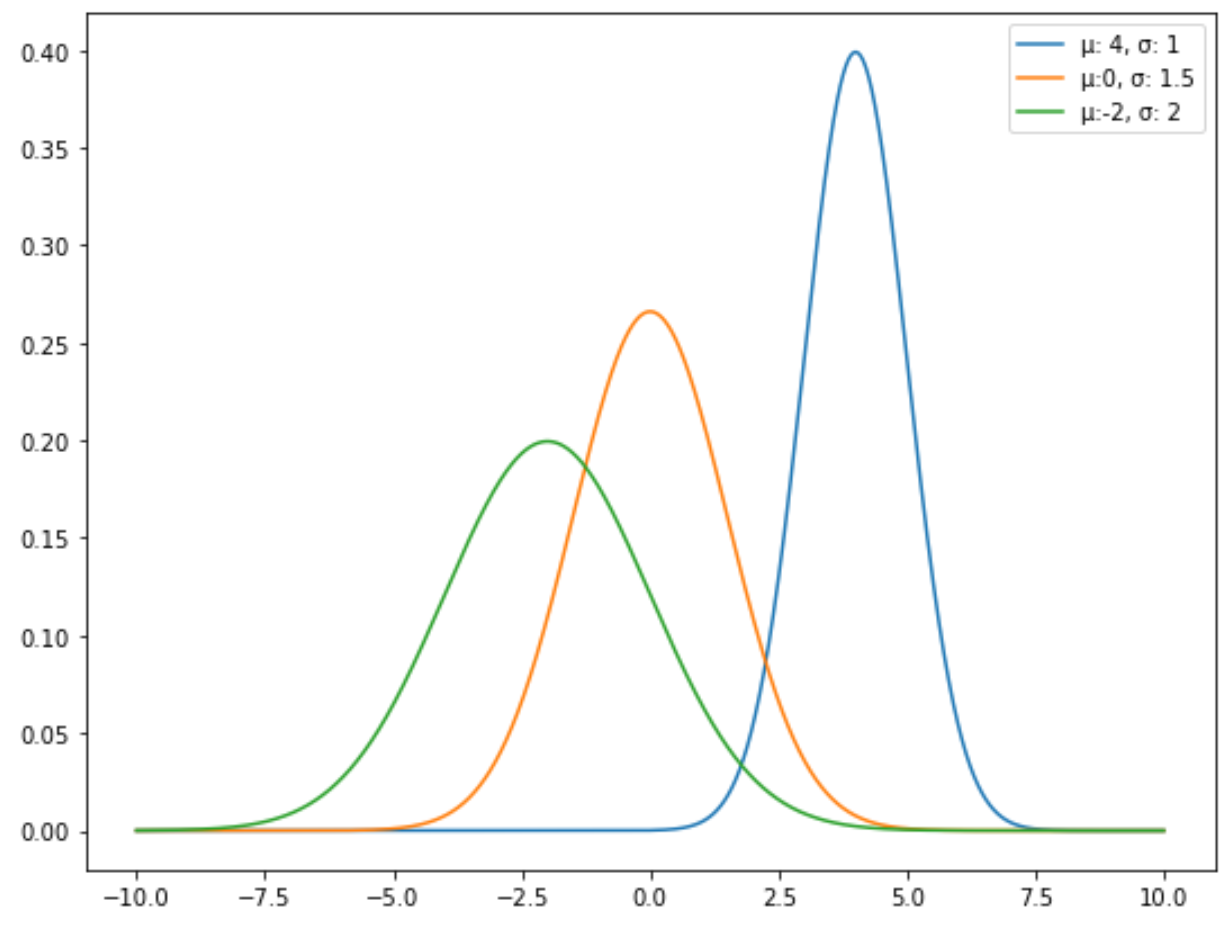
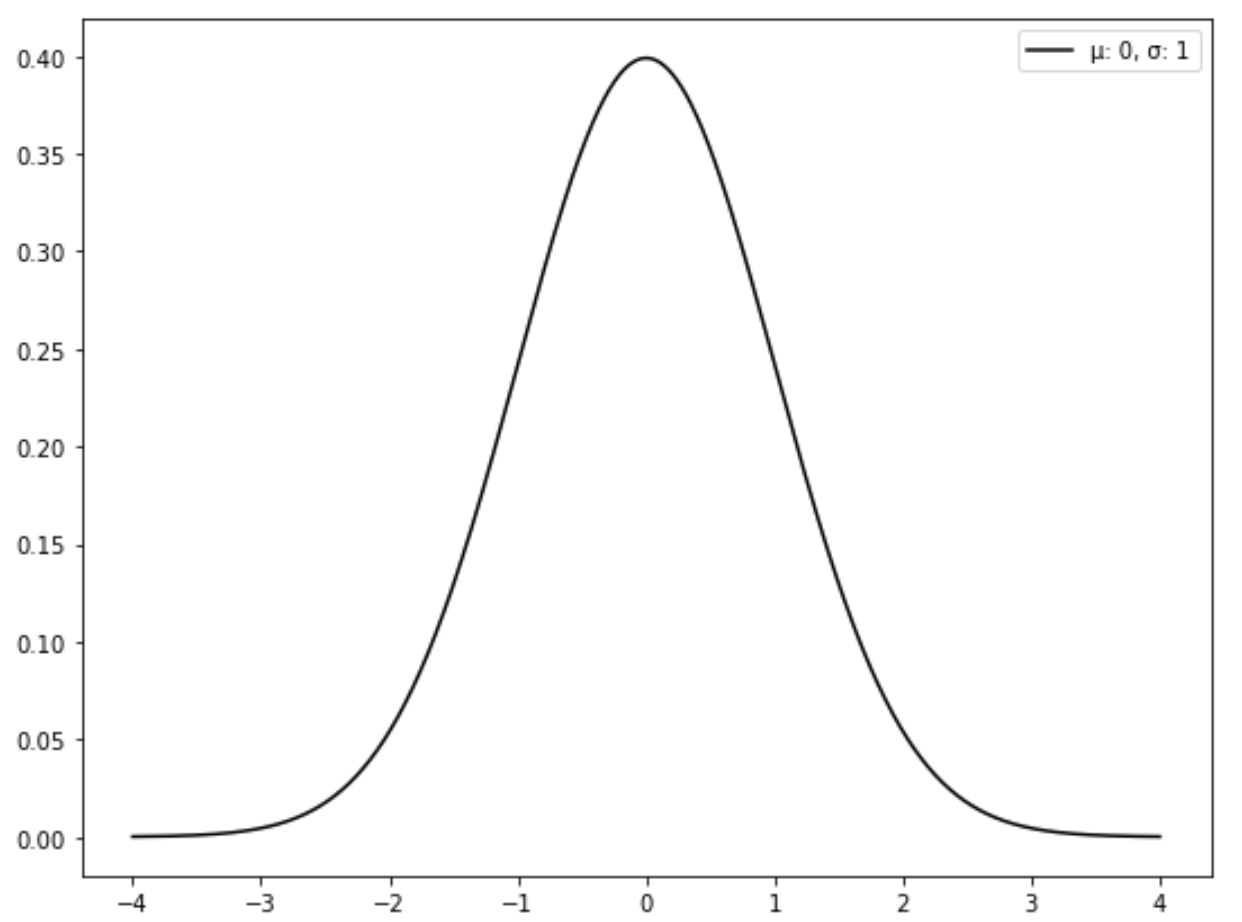
標準正規分布は、平均が 0、標準偏差が 1 である特定の種類の正規分布です。
次のグラフは、標準正規分布を示しています。
正規分布を標準正規分布に変換する方法
次の式を使用してデータ値を Z スコアに変換することで、任意の正規分布を標準正規分布に変換できます。
z = (x – μ) / σ
金:
- x:個別データの値
- μ:分布の平均
- σ:分布の標準偏差
たとえば、平均が 6、標準偏差が 2.152 の次のデータ セットがあるとします。
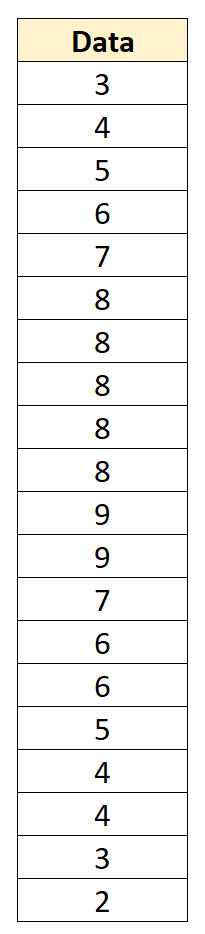
各値から 6 を引いて 2.152 で割ることにより、個々のデータ値を Z スコアに変換できます。
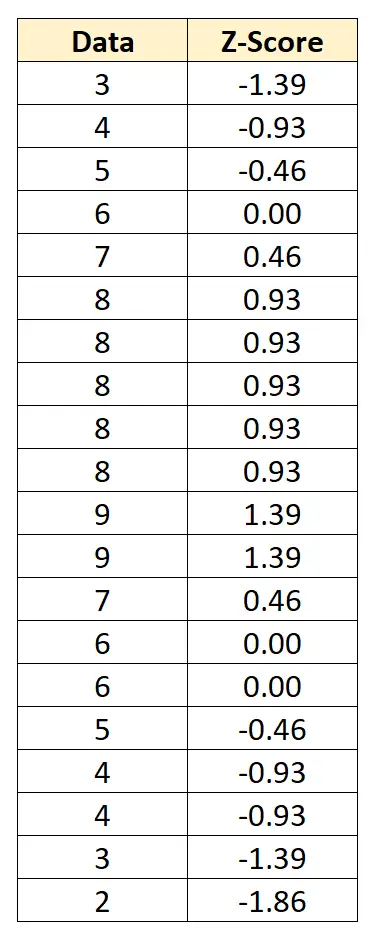
Z スコアは、各データ ポイントが平均からどれだけ標準偏差があるかを示します。たとえば、最初のデータ値「3」は平均より 1.39 標準偏差低いです。
このスコア分布の平均値は 0、標準偏差は 1 です。
標準正規分布の使用方法
標準正規分布には次の特性があります。
- データの約 68% が平均値の 1 標準偏差以内に収まります
- データの約 95% は平均値の 2 標準偏差以内に収まります。
- データの約 99.7% が平均値の 3 標準偏差以内に収まります。

これは経験則として知られており、データセット内の値の分布を理解するために使用されます。
たとえば、ある庭園の植物の高さが平均 47.4 インチ、標準偏差 2.4 インチで正規分布しているとします。
経験則を使用すると、高さ 54.6 インチ未満の植物は何パーセントになりますか?
経験則によれば、正規分布を持つ特定のデータセットでは、データ値の 99.7% が平均の 3 標準偏差以内に収まります。これは、値の 49.85% が平均と平均を上回る 3 標準偏差の間にあることを意味します。
この例では、54.6 は平均より 3 標準偏差上です。正規分布ではデータ値の 50% が平均より小さいことがわかっているため、合計 50% + 49.85% = 99.85% の値は 54.6 より小さくなります。
つまり、植物の99.85%は高さ 54.6 インチ未満です。