正規分布
正規分布は、統計において最も一般的な確率分布です。
正規分布には次のような特徴があります。
- ベル型
- 対称
- 平均と中央値は等しいです。どちらも分布の中心に位置します
- データの約 68% が平均値の 1 標準偏差以内に収まります
- データの約 95% は平均値の 2 標準偏差以内に収まります。
- データの約 99.7% が平均値の 3 標準偏差以内に収まります。
最後の 3 つのポイントは経験則として知られており、 68-95-99.7 ルールと呼ばれることもあります。
関連:経験則 (実践問題)
正規曲線の描き方
正規曲線を描くには、平均と標準偏差を知る必要があります。
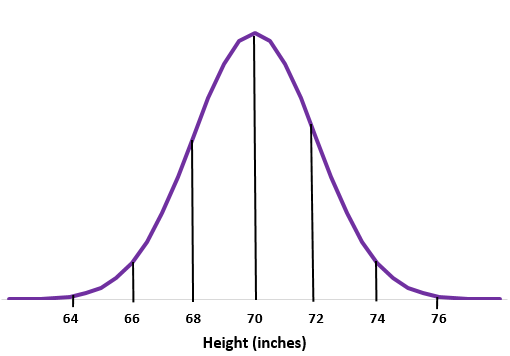
例 1:特定の学校の男性の身長が、平均標準偏差
ステップ 1:通常の曲線をスケッチします。
ステップ 2:平均 70 インチが真ん中にあります。
ステップ 3:各標準偏差は 2 インチの距離に対応します。
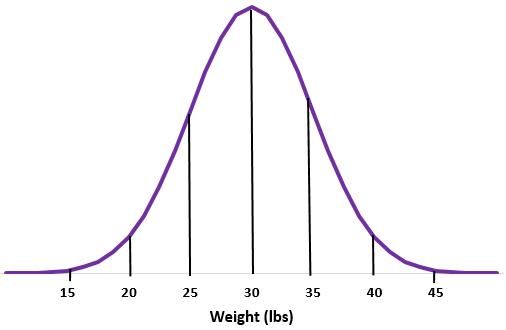
例 2:特定の種のカワウソの体重が平均標準偏差で正規分布すると仮定します。
ステップ 1:通常の曲線をスケッチします。
ステップ 2:平均 30 ポンドは真ん中にあたります。
ステップ 3:各標準偏差は 5 ポンドの距離に対応します
正規分布を使用してパーセンテージを求める方法
68-95-99.7 ルールとも呼ばれる経験則では、正規分布する確率変数の場合、データの 68% が平均から 1 標準偏差の範囲内に収まり、95% が 2 標準偏差の範囲内に収まると述べています。平均からの偏差、および 99.7% は平均から 3 標準偏差以内にあります。
このルールを使用すると、パーセンテージに関する質問に答えることができます。
例:特定の学校の男子の身長が平均標準偏差
解決：
ステップ 1:平均標準偏差
ステップ 2: 74 インチの身長は、平均より 2 標準偏差上です。この点を超えるパーセンテージを正規分布に追加します。
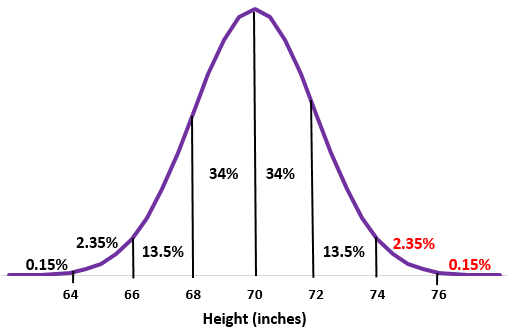
2.35% + 0.15% = 2.5%
この学校の男性の約2.5%は身長 74 インチを超えています。
解決：
ステップ 1:平均標準偏差
ステップ 2:身長 68 インチと 72 インチは、それぞれ平均より 1 標準偏差低く、平均より上です。正規分布におけるこれら 2 つの点の間のパーセンテージを加算するだけです。
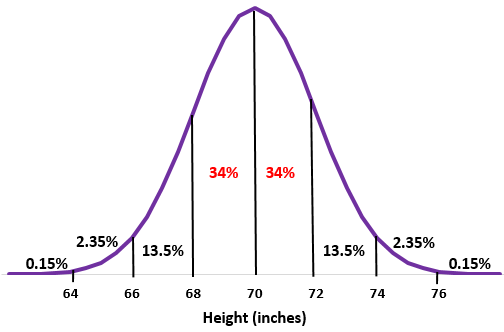
34% + 34% = 68%
この学校の男子生徒の約68%の身長は 68 インチから 72 インチの間です。
正規分布を使用してカウントを見つける方法
経験則を使用して、カウントに関する質問に答えることもできます。
例:特定の種のカワウソの体重が平均標準偏差で正規分布すると仮定します。
あるコロニーにはこのカワウソが200頭います。これらのカワウソのうち、体重が 35 ポンドを超えるのはおよそ何匹でしょうか?
解決：
ステップ 1:平均標準偏差の正規分布をスケッチします。
ステップ 2:体重 35 ポンドは、平均より標準偏差 1 つ大きい値です。この点を超えるパーセンテージを正規分布に追加します。
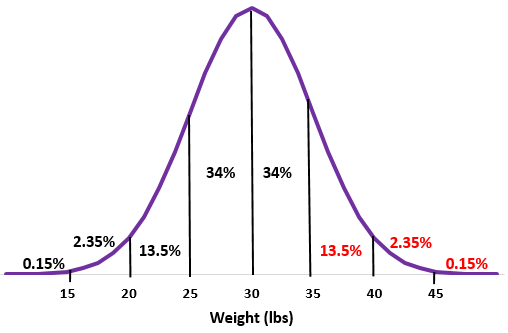
13.5% + 2.35% + 0.15% = 16%
ステップ 3:コロニーには 200 頭のカワウソがいるため、200 の 16% = 0.16 * 200 = 32
このコロニーには体重が 35 ポンドを超えるカワウソが約 32 頭います。
このコロニーには体重が 30 ポンド未満のカワウソがおよそ何匹いますか?
上記で実行したすべての手順に従う代わりに、正規分布の中央値が平均値に等しいことを認識できます。この場合、それは 30 ポンドです。
これは、カワウソの半分の体重が30ポンドを超え、残りの半分の体重が30ポンド未満であることを意味します。これは、200 頭のカワウソのうち 50% の体重が 30 ポンド未満であることを意味するため、0.5 * 200 = 100 頭のカワウソとなります。
追加リソース
次のチュートリアルでは、正規分布に関する追加情報を提供します。
正規分布の6つの具体例
正規分布と t 分布: 違い
Excelでベルカーブを作成する方法
Python でベルカーブを作成する方法
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る