Stata で正規性をテストする方法

多くの統計テストでは、テスト結果の信頼性を得るために 1 つ以上の変数が正規分布していることが必要です。

このチュートリアルでは、Stata で変数間の正規性をテストするために使用できるいくつかの方法について説明します。

これらの各メソッドでは、 autoと呼ばれる組み込みの Stata データセットを使用します。次のコマンドを使用して、このデータセットをロードできます。

システムの自動使用

方法 1: ヒストグラム

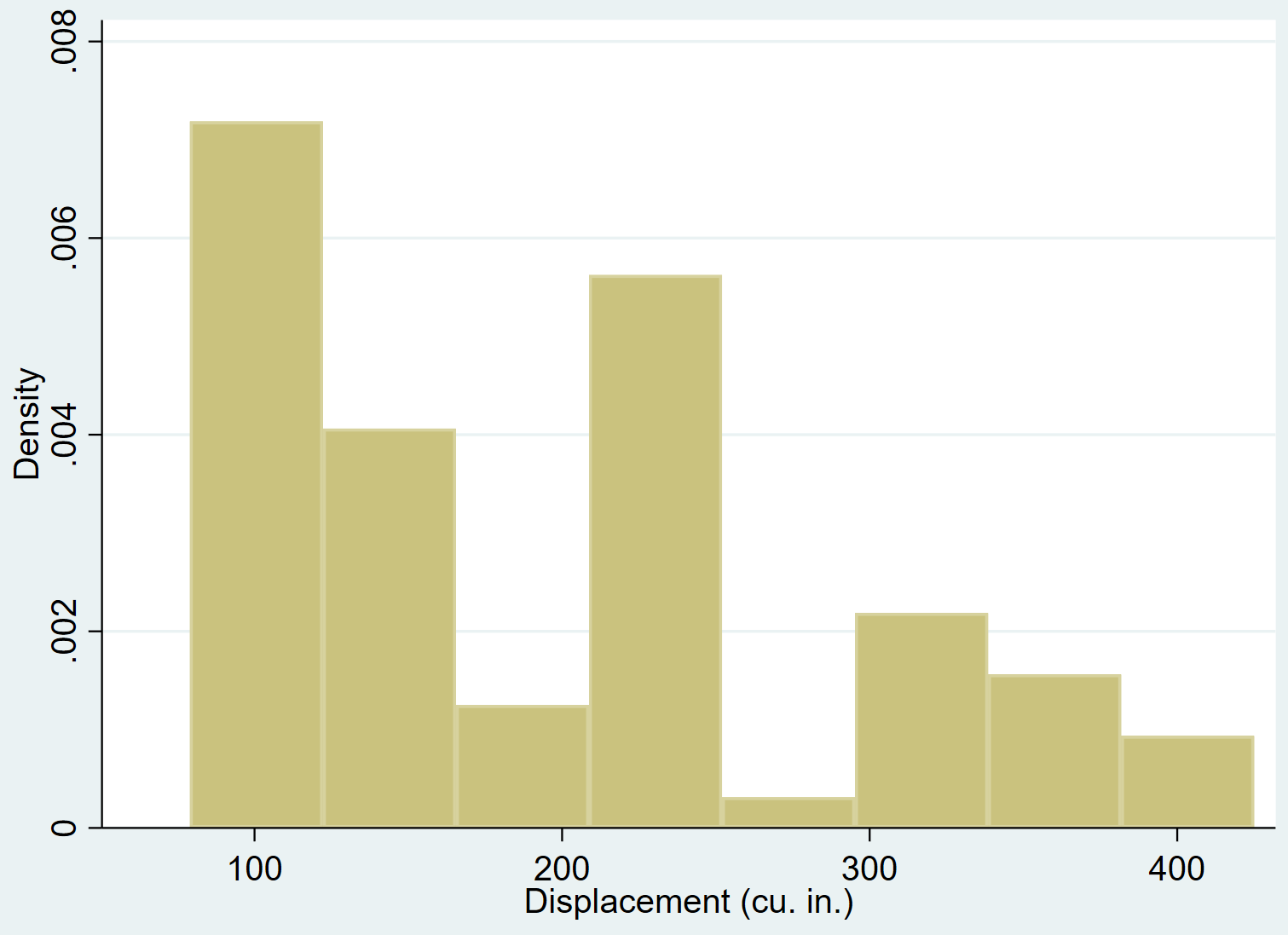
変数が正規分布しているかどうかを確認する非公式な方法は、 ヒストグラムを作成して変数の分布を表示することです。

変数が正規分布している場合、ヒストグラムは中心付近に多くの値が配置され、裾に少ない値が配置される「鐘」の形になります。

histコマンドを使用して、変数displacementのヒストグラムを作成できます。

歴史の移動

通常のコマンドを使用して、ヒストグラムに正規濃度曲線を追加できます。

移動履歴、通常

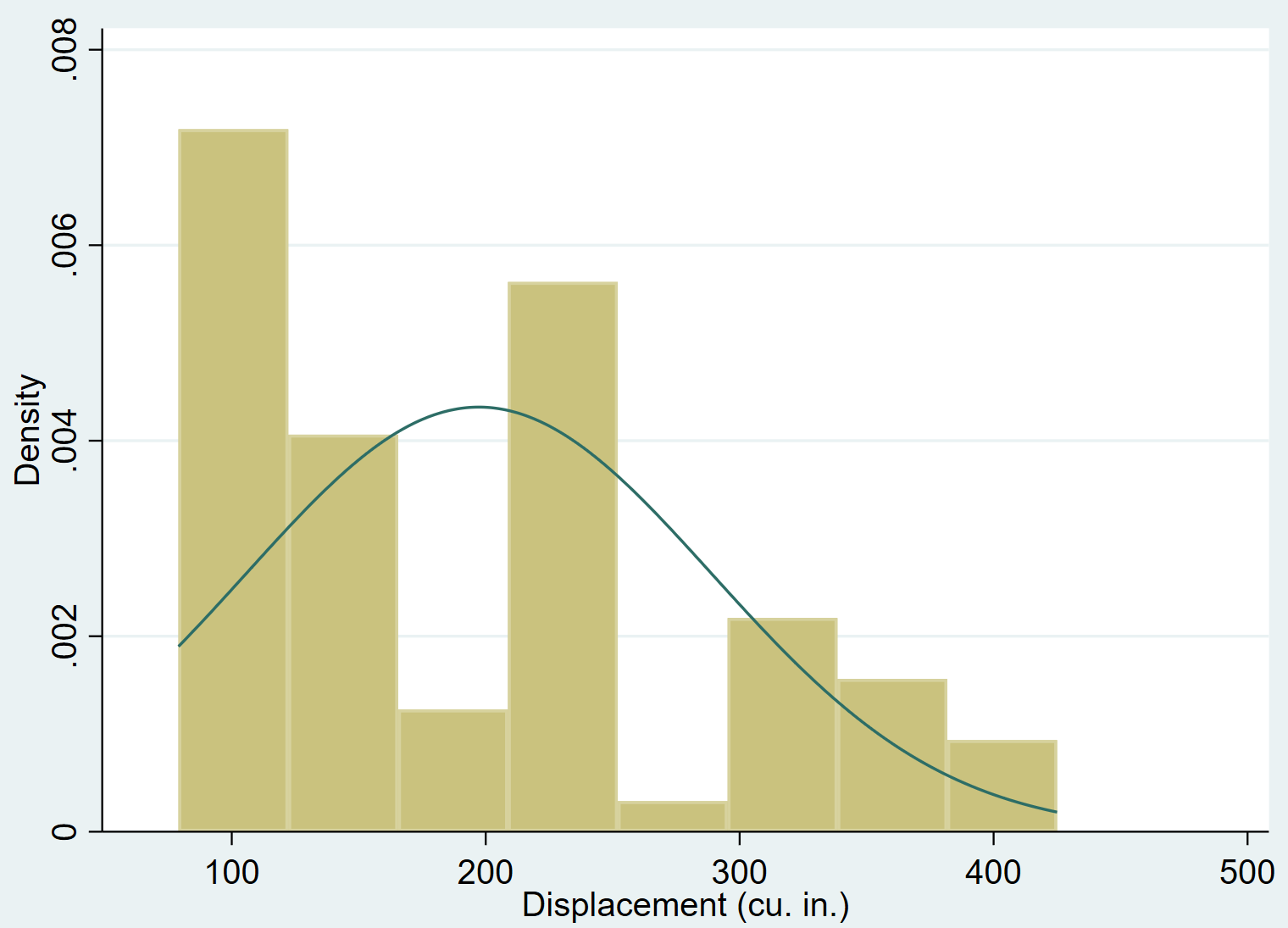
変数のシフトが右に偏っていて (たとえば、ほとんどの値が左側に集中し、値の長い「尾部」が右側に伸びている)、正規分布に従っていないことは明らかです。

関連: 左右に歪んだ分布

方法 2: シャピロ・ウィルク検定

正規性をテストする正式な方法は、 Shapiro-Wilk テストを使用することです。

この検定の帰無仮説は、変数が正規分布するということです。検定のp 値が特定の有意レベル (一般的な選択肢には 0.01、0.05、0.10 など) を下回っている場合、帰無仮説を棄却し、変数が正規分布していないと主張する十分な証拠があると結論付けることができます。 。

※この検定は観測総数が4～2,000の場合に使用できます。

swilkコマンドを使用して、変数displacementに対して Shapiro-Wilk テストを実行できます。

スムーズな動き

テスト結果を解釈する方法は次のとおりです。

Obs: 74。これはテストで使用された観測値の数です。

幅：0.92542。これはテストのテスト統計です。

確率: 0.00031。これは検定統計量に関連付けられた p 値です。

p 値は 0.05 未満であるため、検定の帰無仮説を棄却できます。変数変位が正規分布ではないことを示す十分な証拠があります。

swilkコマンドの後に複数の変数をリストすることで、複数の変数に対して Shapiro-Wilk テストを一度に実行することもできます。

スウィク変位 mpg 長さ

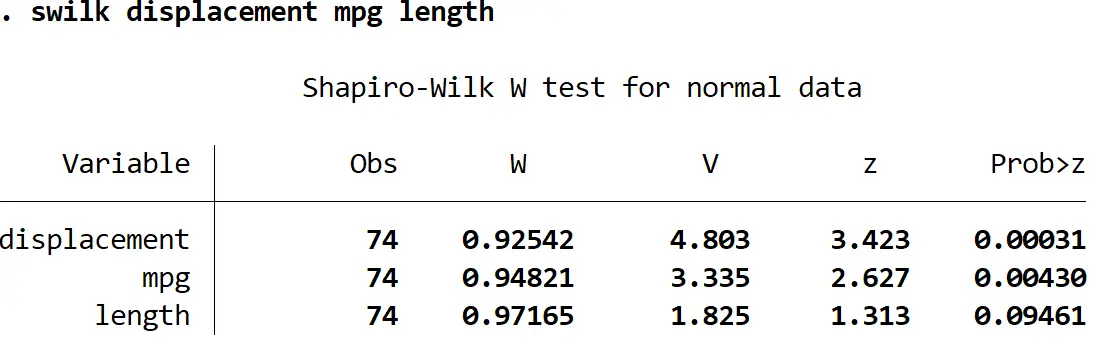
有意水準 0.05 を使用すると、変位とmpgは正規分布していないと結論付けることになりますが、長さが正規分布していないと言える十分な証拠はありません。

方法 3: シャピロ・フランシア検定

正規性をテストするもう 1 つの正式な方法は、 Shapiro-Francia テストを使用することです。

この検定の帰無仮説は、変数が正規分布するということです。検定の p 値が一定の有意レベルを下回っている場合は、帰無仮説を棄却し、変数が正規分布していないと言える十分な証拠があると結論付けることができます。

※この検定は観測総数が10～5,000の場合に使用できます。

sfranciaコマンドを使用して、変数変位に対して Shapiro-Wilk テストを実行できます。

移動スフランシア

テスト結果を解釈する方法は次のとおりです。

Obs: 74。これはテストで使用された観測値の数です。

W’: 0.93011。これはテストのテスト統計です。

確率: 0.00094。これは検定統計量に関連付けられた p 値です。

p 値は 0.05 未満であるため、検定の帰無仮説を棄却できます。変数変位が正規分布ではないことを示す十分な証拠があります。

Shapiro-Wilk テストと同様に、 sfranciaコマンドの後に複数の変数をリストすることにより、複数の変数に対して Shapiro-Francia テストを一度に実行できます。

方法 4: 歪度と尖度のテスト

正規性をテストするもう 1 つの方法は、変数の歪度と尖度が正規分布と一致するかどうかを判断する、歪度と尖度のテストを使用することです。

この検定の帰無仮説は、変数が正規分布するということです。検定の p 値が一定の有意レベルを下回っている場合は、帰無仮説を棄却し、変数が正規分布していないと言える十分な証拠があると結論付けることができます。

*このテストでは、少なくとも 8 つの観測値を使用する必要があります。

sktestコマンドを使用して、変数displacementに対して歪度と尖度テストを実行できます。

テストを移動する

テスト結果を解釈する方法は次のとおりです。

Obs: 74。これはテストで使用された観測値の数です。

adj chi(2): 5.81。これは検定のカイ二乗検定統計量です。

確率χ2: 0.0547。これは検定統計量に関連付けられた p 値です。

p 値は 0.05 未満ではないため、検定の帰無仮説を棄却できません。動きが正規分布ではないと言える十分な証拠はありません。

他の正規性検定と同様に、 sktestコマンドの後に複数の変数をリストすることにより、複数の変数に対して歪度および尖度検定を一度に実行できます。