標準正規分布
この記事では、標準正規分布とは何か、またそれが何に使用されるのかについて説明します。標準正規分布のプロパティ、その特性値を含む表、さらに解決された演習も見つかります。
標準正規分布とは何ですか?
標準正規分布 は、単位正規分布とも呼ばれ、正規分布の最も単純なケースです。より正確には、標準正規分布は、平均値と標準偏差値がそれぞれ 0 と 1 に等しい正規分布です。
したがって、標準正規分布は N(0,1) として定義されます。ここで、最初のパラメーターは分布の平均、2 番目のパラメーターはその標準偏差 (または SD) です。
![Rendered by QuickLaTeX.com \displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ca26cb58ac445099df12aeebda27e38_l3.png)
したがって、標準正規分布のグラフは次のようになります。
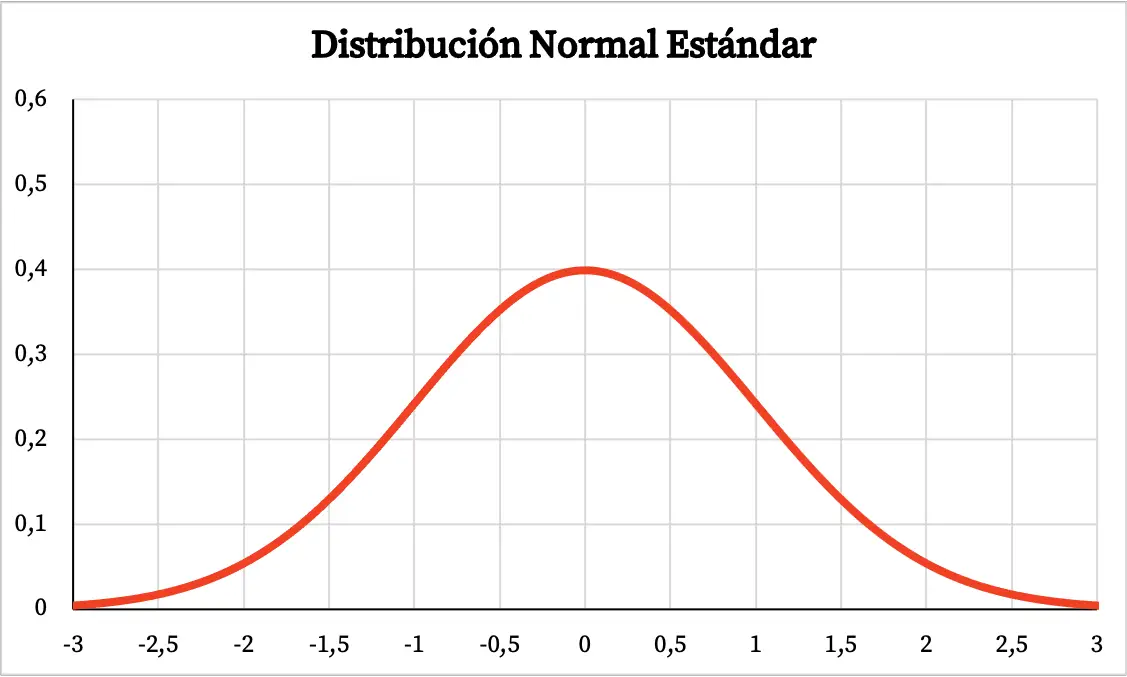
標準正規分布の公式
正規分布を標準正規分布に変換するには、正規分布のすべての値から正規分布の平均を減算し、正規分布の標準偏差で割る必要があります。
したがって、標準正規分布の式は次のようになります。
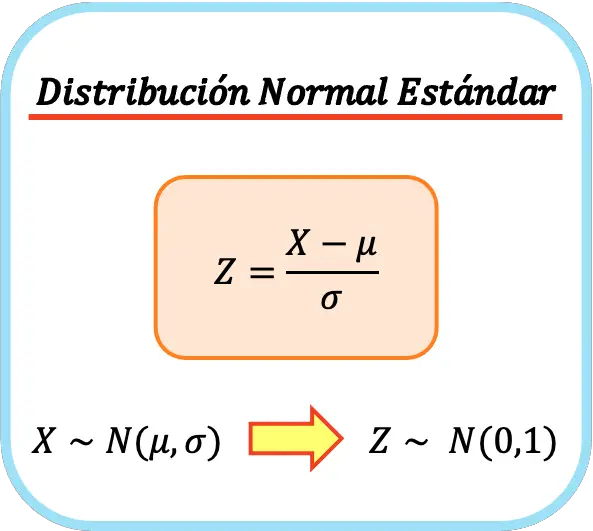
このようにして、新しい変数の算術平均と標準偏差はそれぞれ 0 と 1 になり、標準正規分布が得られます。このプロセスは、一変量正規化または一変量正規化とも呼ばれます。
標準正規分布表
標準正規分布の表は、観測値が標準正規分布の所定の値より小さい確率を含む表です。
さらに、正規分布の関数は平均と標準偏差に依存するため、標準正規分布表は、拡張して正規分布の確率を決定するためにも使用されます。これを行うには、正規分布を標準正規分布に入力し、テーブル内でそれに対応する確率を調べます。
したがって、標準正規分布表の値は次のようになります。

標準正規分布の例
標準正規分布の定義とその式が何であるかを理解したところで、概念をよく理解するために以下に具体的な例を示します。
- 連続確率変数は、平均 45、標準偏差 15 の正規分布に従います。58 以下の値が得られる確率はどれくらいですか?
![]()
正規分布の確率を見つけるには、その特徴テーブルを使用する必要がありますが、そのためには、まず標準正規分布を取得するための型付けプロセスを実行する必要があります。したがって、標準の正規分布式を使用します。
![]()
したがって、確率値から平均を引いて、標準偏差で割ります。
![]()
変数を標準化したら、標準正規分布確率テーブル (上記を参照) に移動して、値 0.87 がどの確率に対応するかを確認します。
![]()
したがって、58 以下の値が得られる確率は 80.78% になります。
標準正規分布の特徴
標準正規分布には次の特徴があります。
- 標準正規分布は、0 を中心とする対称分布です。
- 正規分布と同様に、標準正規分布グラフは釣鐘型で、グラフ領域のほとんどが平均値付近にあります。
- したがって、正規分布の平均、最頻値、中央値は同じ値、つまり 0 になります。
- 標準正規分布は z=0 で最大値を持ちます。
- 同様に、標準正規分布には、z=-1 と z=+1 に 2 つの変曲点があります。
- 経験則によれば、値の 68% が +1 と -1 の間の標準正規分布に収まり、値の 95% が +2 と -2 の間、値の 99.7% が +2 と -1 の間の標準分布に収まることがわかります。 3と-3。