Sas で段階的回帰を実行する方法 (例あり)
段階的回帰は、統計的に有効な入力または入力の理由がなくなるまでモデルに段階的に予測子を入力および削除することにより、一連の予測子変数から回帰モデルを構築するために使用できる手順です。さらに削除します。
段階的回帰の目的は、 応答変数と統計的に有意に関連するすべての予測変数を含む回帰モデルを作成することです。
SAS で段階的回帰を実行するには、 PROC REG をSELECTIONステートメントとともに使用します。
次の例は、実際に SAS で段階的回帰を実行する方法を示しています。
例: SAS でのステップバイステップ回帰の実行
SAS に、4 つの予測変数 (x1、x2、x3、x4) と 1 つの応答変数 (y) を含む次のデータセットがあるとします。
/*create dataset*/ data my_data; input x1 x2 x3 x4 y; datalines ; 1 4 10 13 78 2 4 12 14 81 5 3 7 10 75 8 2 13 9 97 10 5 12 5 95 14 7 8 6 90 17 8 10 6 86 19 5 15 5 90 20 5 12 4 93 21 4 10 3 95 ; run ; /*view dataset*/ proc print data =my_data;
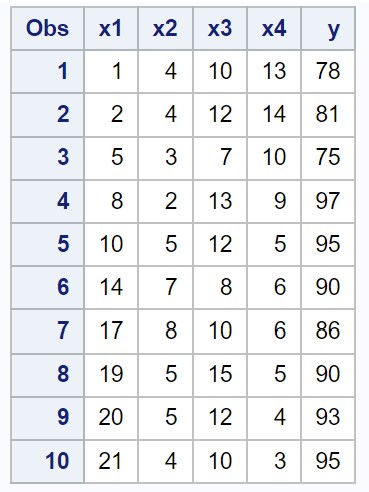
ここで、予測子変数のどの組み合わせが最良の重線形回帰モデルを生成するかを判断したいとします。
「最適な」回帰モデルについて話すときは、特定の尺度を最大化または最小化するモデルを意味します。
潜在的なモデルのグループの中でどの回帰モデルが最適であるかを評価するために一般的に使用される 2 つの指標があります。
1. 調整された R 二乗:調整された R 二乗値は、モデル内の予測子の数に基づいて調整されたモデルの有用性を示します。調整された R 二乗値が最も高いモデルが最良とみなされます。
2. AIC :赤池情報量基準(AIC) は、さまざまな回帰モデルの適合度を比較するために使用される指標です。 AIC 値が最も低いモデルが最良とみなされます。
幸いなことに、SAS ではPROC REGとSELECTIONステートメントを使用して、回帰モデルの近似 R 二乗値と AIC 値の両方を計算できます。
次のコードは、これを行う方法を示しています。
/*perform stepwise multiple linear regression*/ proc reg data =my_data outest =est; model y=x1 x2 x3 x4 / selection=adjrsq aic ; output out =out p=pr=r; run ; quit ;
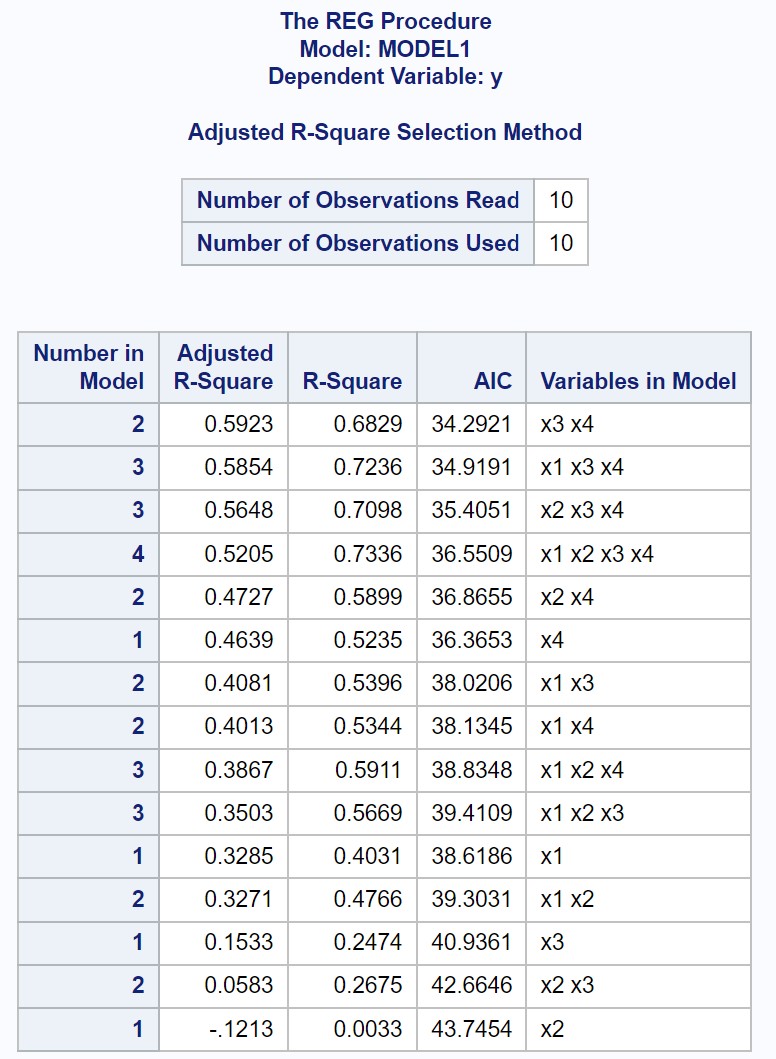
出力には、考えられる各重線形回帰モデルの近似 R 二乗値と AIC 値が表示されます。
結果から、調整後の R 二乗値が最も高く、 AIC 値が最も低い値は、予測変数として x3 と x4 のみを使用する回帰モデルであることがわかります。
したがって、次のモデルがすべての可能なモデルの中で「最良」であると宣言します。
y = b 0 + b 1 (x3) + b 2 (x4)
この特定の回帰モデルには次のメトリクスがあります。
- 調整後の R 二乗値: 0.5923
- AIC: 34.2921
「最適な」回帰モデルの選択に関する注意事項
調整された R 二乗値が最も高いモデルが、必ずしも AIC 値が最も低いとは限らないことに注意してください。
どの回帰モデルが最適であるかを決定する場合、調整された R 二乗と AIC が候補として機能しますが、実際の世界では、どのモデルが最適であるかを決定するには、その分野の専門知識を使用する必要がある場合があります。
また、倹約的なモデル、つまり、できるだけ少ない予測子変数を使用して望ましいレベルの適合を達成するモデルを選択することも賢明な場合があります。
このタイプのモデルの背後にある推論は、最も単純な説明がおそらく正しいという オッカムのかみそりの考え方 (「倹約原則」とも呼ばれます) に由来しています。
統計に当てはめると、パラメータがほとんどなくても満足のいくレベルの適合を達成するモデルは、大量のパラメータを持ち、わずかに高いレベルの適合のみを達成するモデルよりも優先されるべきです。
追加リソース
次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。
SAS で単純な線形回帰を実行する方法
SAS で重回帰を実行する方法
SAS で多項式回帰を実行する方法
SAS でロジスティック回帰を実行する方法