Sas で roc 曲線を作成する方法
ロジスティック回帰は、応答変数がバイナリの場合に回帰モデルを近似するために使用できる方法です。
ロジスティック回帰モデルがデータセットにどの程度適合しているかを評価するには、次の 2 つの指標を確認します。
- 感度:結果が実際に肯定的な場合に、モデルが観測値に対して肯定的な結果を予測する確率。これは「真陽性率」とも呼ばれます。
- 特異性:結果が実際には陰性である場合に、モデルが観測値に対して陰性の結果を予測する確率。これは「真のネガティブ率」とも呼ばれます。
これら 2 つの測定値を視覚化する 1 つの方法は、「受信機動作特性」曲線を表すROC 曲線を作成することです。これは、ロジスティック回帰モデルの感度と特異度を表示するグラフです。
次のステップバイステップの例は、SAS で ROC 曲線を作成および解釈する方法を示しています。
ステップ 1: データセットを作成する
まず、18 人の生徒の次の変数に関する情報を含むデータセットを作成します。
- 特定の大学への合格 (1 = はい、0 = いいえ)
- GPA (1 ~ 4 のスケール)
- ACT スコア (1 ~ 36 のスケール)
/*create dataset*/ data my_data; input acceptance gpa act; datalines ; 1 3 30 0 1 21 0 2 26 0 1 24 1 3 29 1 3 34 0 3 31 1 2 29 0 1 21 1 2 21 0 1 15 1 3 32 1 4 31 1 4 29 0 1 24 1 4 29 1 3 21 1 4 34 ; run ;
ステップ 2: ロジスティック回帰モデルを当てはめて ROC 曲線を作成する
次に、 proc ロジスティックスを使用して、応答変数として「acceptance」、予測変数として「gpa」と「act」を使用して、ロジスティック回帰モデルを当てはめます。
応答変数が値 1 を取る確率を SAS が予測する方法を認識できるように、減少を指定します。
また、 plots(only)=rocを使用してモデルの ROC 曲線を作成します。
/*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
model acceptance = gpa act;
run ;
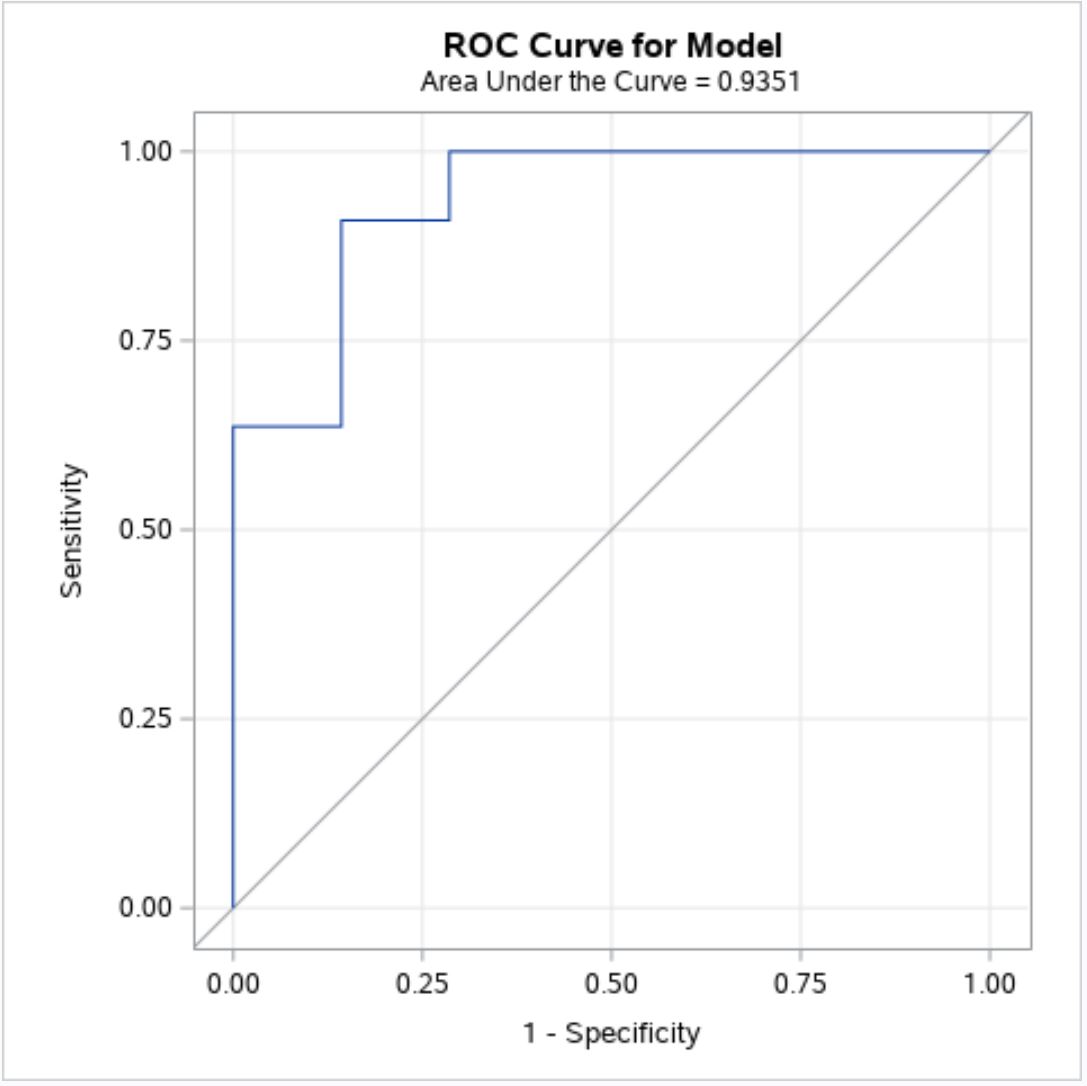
ステップ 3: ROC 曲線を解釈する
ROC 曲線がプロットの左上隅に近ければ近いほど、モデルはデータセット内の応答値の値をより適切に予測します。
上のグラフから、青い ROC 曲線が左上隅に一致する傾向があることがわかり、ロジスティック回帰モデルが応答値の値を適切に予測していることを示しています。
ロジスティック回帰モデルがデータにどの程度適合しているかを定量化するには、 AUC (曲線下面積) を計算します。これにより、プロットのどの程度が曲線の下にあるかがわかります。
AUC が 1 に近づくほど、モデルは優れています。 AUC が 0.5 に等しいモデルは、ランダムな分類を行うモデルと同等です。
上のチャート タイトルの下で、このモデルの AUC が0.9351であることがわかります。
この値は 1 に近いため、モデルが応答値の値を適切に予測していることが確認されます。
AUC 値を使用して、さまざまなロジスティック回帰モデルの適合を比較することもできます。
たとえば、2 つの異なるロジスティック回帰モデルを当てはめ、それぞれの AUC 値を計算するとします。
- モデル 1 の AUC: 0.9351
- モデル 2 の AUC: 0.8140
モデル 1 の AUC が大きいため、これは、モデル 1 がモデル 2 よりもデータの適合に優れていることを示しています。
追加リソース
次のチュートリアルでは、SAS で他の一般的な操作を実行する方法について説明します。