Stata でフィッシャーの正確確率検定を実行する方法
フィッシャーの直接確率検定は、 2 つのカテゴリ変数間に有意な関連があるかどうかを判断するために使用されます。これは通常、2 × 2 テーブル内の 1 つ以上のセル数が 5 未満である場合に、 独立性のカイ二乗検定の代替として使用されます。
このチュートリアルでは、Stata でフィッシャーの正確確率検定を実行する方法について説明します。
例: Stata でのフィッシャーの正確確率検定
特定の大学での政党への選好に性別が関連しているかどうかを知りたいとします。これを調査するために、キャンパス内の 25 人の学生をランダムに調査しました。性別に基づいた民主党または共和党の学生数を以下の表に示します。
| 民主党 | 共和党 | |
|---|---|---|
| 男 | 4 | 9 |
| 女性 | 8 | 4 |
性別と政党の好みの間に統計的に有意な関連があるかどうかを判断するには、フィッシャーの正確確率検定を実行できます。
Stata では、 tabiコマンドを使用してフィッシャーの正確確率検定を実行できます。 2×2 テーブルに左から右にカウントを入力し、 \ を使用して上下の行を区切ります。
足袋 4 9 \ 8 4
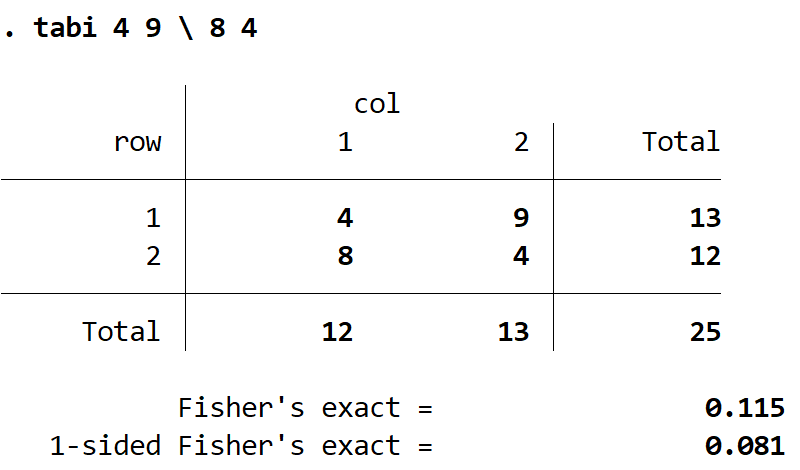
結果を解釈する方法は次のとおりです。
出力テーブル:このテーブルには、入力した各セルの数が表示されます。
フィッシャーの正確確率:これは、両側フィッシャーの正確確率検定に関連付けられた p 値です。この場合は 0.115 です。
片側フィッシャーの正確確率:これは、片側フィッシャーの正確確率検定に関連付けられた p 値です。この場合は 0.081 です。
フィッシャーの正確検定の帰無仮説は、2 つの変数が独立であるということです。この場合、帰無仮説は性別と政党の好みが独立しているということであり、これは両側検定であるため、最初の p 値 0.115 を使用します。
この p 値は 0.05 未満ではないため、帰無仮説は棄却されません。したがって、性別と政党の好みの間に重大な関連があると言える十分な証拠はありません。