相互に包括的なイベントまたは相互に排他的なイベント

2 つのイベントは、同時に発生できない場合、相互に排他的です。

たとえば、イベント A がサイコロの目が偶数になるイベントであり、イベント B がサイコロの目が奇数になるイベントであるとします。

イベントのサンプル空間を次のように定義します。

• A = {2, 4, 6}
• B = {1, 3, 5}

2 つのサンプリングされた空間の間に重なりがないことに注意してください。したがって、イベント A と B は同時に発生できないため、相互に排他的です。サイコロの目が偶数と奇数の両方になることはできません。

逆に、2 つのイベントが同時に発生する可能性がある場合、これらのイベントは相互に包含されます。

たとえば、イベント C をサイコロが偶数の目に出るイベント、イベント D をサイコロが 3 より大きい数字に出るイベントだとします。

イベントのサンプル空間を次のように定義します。

• C = {2、4、6}
• d = {4, 5, 6}

2 つのサンプリングされた空間の間には重複があることに注意してください。したがって、イベント C と D は同時に発生する可能性があるため、両方とも包括的です。サイコロが 3 より大きい偶数の目に出る可能性があります。

事象の確率

2 つのイベントが相互に排他的である場合、両方が発生する確率はゼロです。

たとえば、上記のイベント A と B の 2 つのスペースの例を考えてみましょう。

• A = {2, 4, 6}
• B = {1, 3, 5}

サンプル空間には重複がないため、 P(A および B) = 0と言えます。

しかし、2 つのイベントが相互に包含される場合、それらの両方が発生する確率は 0 より大きい数値になります。

たとえば、前述のイベント C と D の 2 つのスペースの例を考えてみましょう。

• C = {2、4、6}
• d = {4, 5, 6}

サイコロが当たる可能性のある数字は 6 つあり、それらの数字のうち 2 つ (4 と 6) はイベント C と D の両方に属するため、 P(C と D) は 2/6 または1/3として計算されます。

相互に包括的なイベントと相互排他的なイベントを表示する

私たちはイベントに関連する確率を視覚化するためにベン図をよく使用します。

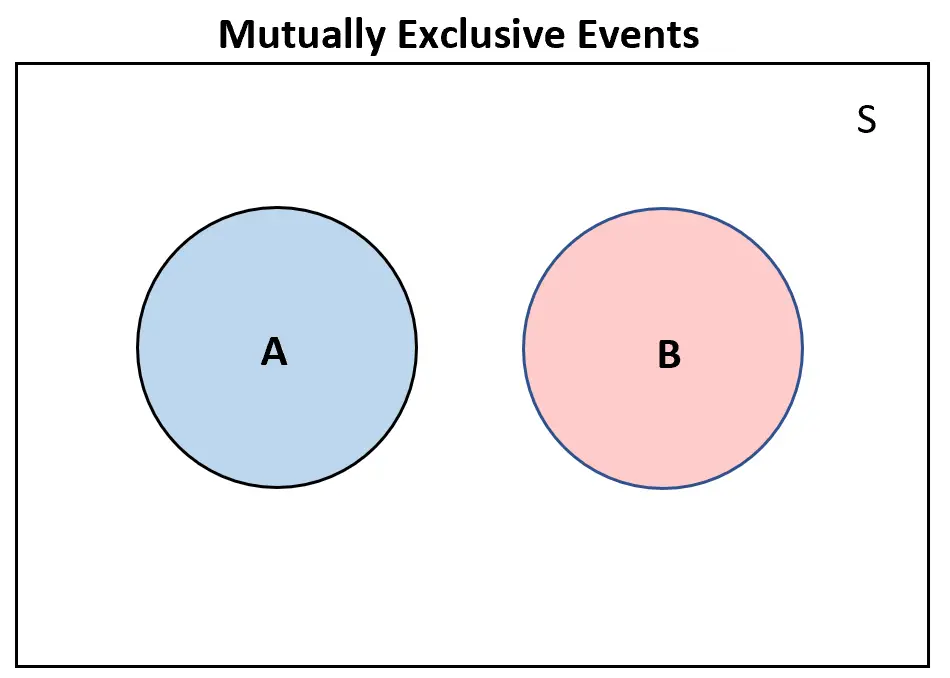
2 つのイベントが相互に排他的である場合、ベン図ではまったく重なりません。

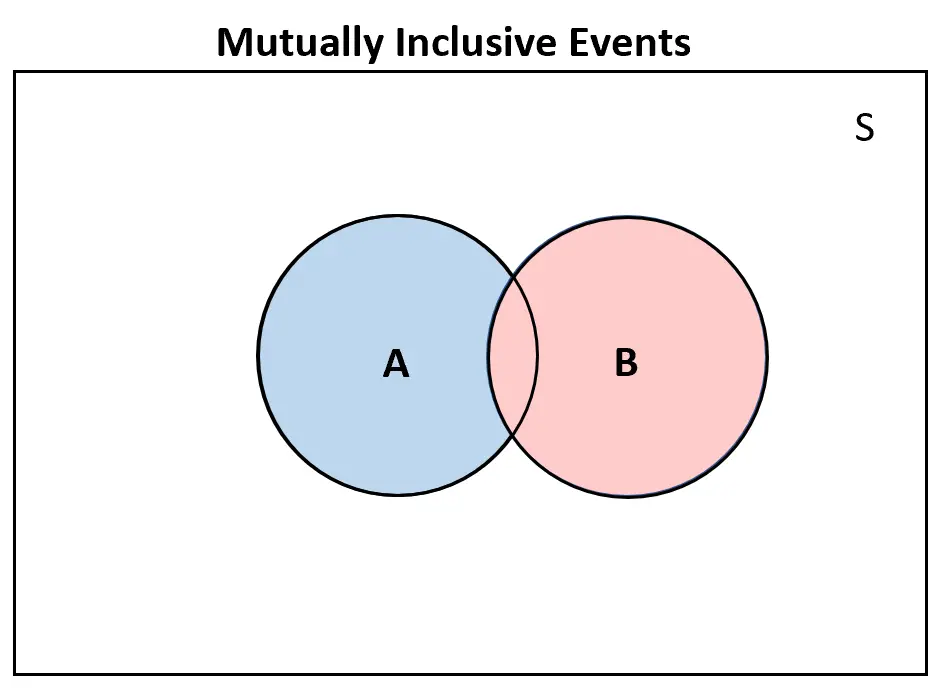
逆に、2 つのイベントが相互に包含される場合、ベン図には少なくとも一部の重複が存在します。

追加リソース

理論的確率の概要
掛け算の一般的な規則
ばらばらなイベントとは何ですか?