相対標準偏差

この記事では、相対標準偏差の計算方法について説明します。相対標準偏差が何であるか、その公式が何であるか、また段階的に解決される演習がわかります。

相対標準偏差とは何ですか?

相対標準偏差は、平均に対するデータセットの分散を示す統計的尺度です。相対標準偏差は、データの標準偏差を平均で割ることによって計算されます。

相対標準偏差はパーセンテージで表され、その値は常に正になります。

相対標準偏差の解釈は、データ サンプルの分散を示すために使用されます。相対標準偏差の値が大きいほど、データはより分散しています。相対標準偏差が小さいほど、データは平均値に近づきます。

一般に、頭字語 RSD は相対標準偏差の記号として使用されます。

相対標準偏差の式

相対標準偏差は、標準偏差を平均値で割った値に 100 を乗算した値に等しくなります。したがって、相対標準偏差を計算するには、まず標準偏差と算術平均を求め、次に 2 つの統計的測定値を割って、最後に 100 を掛ける必要があります。

つまり、相対標準偏差の式は次のようになります。

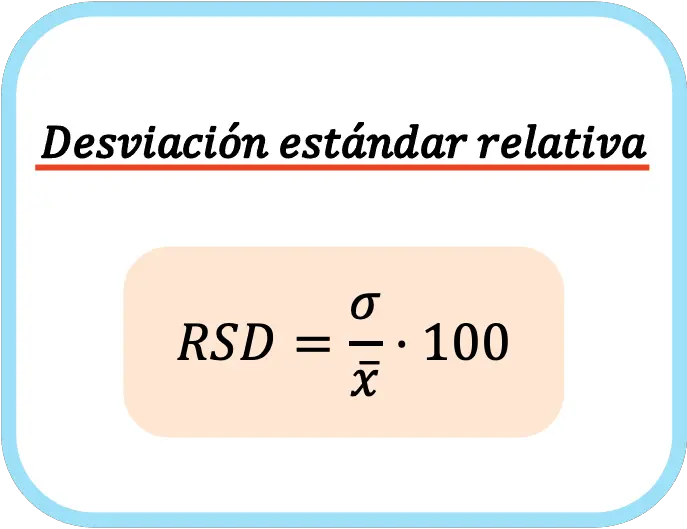
相対標準偏差を計算する場合、値を百分率で表すために 100 を掛けます。

相対標準偏差の計算例

相対標準偏差の定義とその式を確認した後、以下に相対標準偏差の計算方法の具体例を示します。

• 次の統計データ セットの相対標準偏差を計算します。
  4、1、3、9、12、2、5、8、3、6

まず、データの標準偏差を見つける必要があります。

次に、データの算術平均を計算します。

データ系列の標準偏差と算術平均がわかったら、相対標準偏差の式を使用します。

最後に、計算された値を式に代入し、相対標準偏差を計算します。