相関行列
この記事では、相関行列とは何か、その公式とは何か、そして相関行列を解釈する方法について説明します。さらに、相関行列の解釈の具体例も確認できます。
相関行列とは何ですか?
相関行列は、位置i,jに変数iとjの間の相関係数を含む行列です。
したがって、相関行列は主対角上の 1 で満たされた正方行列となり、行iと列jの要素は変数iと変数jの間の相関係数の値で構成されます。
したがって、相関行列の式は次のようになります。

金
![]()
変数間の相関係数です
![]()
そして
![]()
したがって、データセットの相関行列を見つけるには、相関係数がどのように計算されるかを知ることが不可欠です。覚えていない場合は、次のリンクでオンライン計算機を使用して計算する方法をご覧ください。
相関係数の特性は、変数の順序がその計算、つまり相関係数に関係ないことです。
![]()
と同等です
![]()
したがって、相関行列は対称になります。
![Rendered by QuickLaTeX.com \displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-76d9753ac0f42dcdc12ea4b719f37750_l3.png)
相関行列が意味を持つためには、統計データ セットに 3 つ以上の変数が含まれている必要があります。それ以外の場合は、単一の相関係数を決定するだけで十分であり、相関行列は意味のあるものになります。
相関行列の作り方
相関行列の定義を踏まえて、このタイプの統計行列がどのように作成されるかを見てみましょう。
- 変数の各ペアの相関係数を計算します。変数の順序によって結果は変化しないため、変数のペアごとに 1 回だけ計算する必要があることに注意してください。
- データ系列内の変数の数と同じ次元の正方行列を作成します。この行列が相関行列になります。
- 相関行列の主対角の各要素に 1 を入れます。
- 変数i 、 jの相関係数を位置i 、 jおよびj 、 iに置きます。
- 相関行列が作成されたら、あとはその値を解釈するだけです。
単に相関行列を実行するだけでは不十分であることに留意してください。その後、その値を解釈し、その意味を理解する必要があります。次のセクションでは、相関行列を解釈する方法について説明します。
相関行列の解釈
相関行列を正しく解釈するには、相関係数の値が -1 から +1 の範囲であることを考慮する必要があります。
- r=-1 : 2 つの変数には完全な負の相関があるため、すべての点がリンクする負の傾きを持つ線を描くことができます。
- -1<r<0 : 2 つの変数間の相関関係は負であるため、一方の変数が増加すると他方の変数は減少します。値が -1 に近づくほど、変数の負の関連性が高くなります。
- r=0 : 2 つの変数間の相関は非常に弱く、実際、それらの間の線形関係はゼロです。これは、変数が非線形関係を持つ可能性があるため、変数が独立していることを意味するものではありません。
- 0<r<1 : 2 つの変数間の相関は正で、値が +1 に近づくほど、変数間の関係が強くなります。この場合、一方の変数の値が増加すると、もう一方の変数の値も増加する傾向があります。
- r=1 : 2 つの変数には完全な正の相関関係があります。つまり、正の線形関係があります。
したがって、相関行列を解釈するには、各相関係数を解釈し、異なる結果を比較する必要があります。
こうすることで、どの変数が相互に最も関連しているのか、どの変数が最も重要であるのか、どの変数が実質的に相互に関係がないのかなどがわかるようになります。
相関行列の例
相関行列の構成とそれがどのように解釈されるかを完全に理解するために、このセクションでは相関行列の例を分析します。
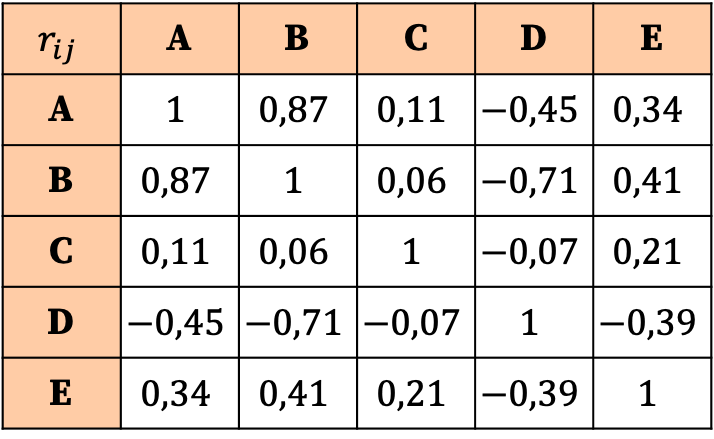
相関行列の解釈は、係数の値に基づいて行われます。したがって、対応する係数が最大 (0.87) であるため、最も強い相関関係は変数 A と変数 B の間の関係であることがわかります。
一方、変数 C は、すべての係数がゼロに非常に近く、したがって非常に低いため、実際にはどの変数とも相関関係がありません。したがって、分析を簡素化するために、統計的研究からこの変数を削除することも検討できます。
同様に、変数 D と他の変数の関係はすべて負であり、変数 D と他の変数の間の相関関係が逆であることを意味します。これは、変数を削除する必要があることを意味するものではなく、単に変数 D が負の相関関係にあることを意味します。
ご覧のとおり、相関行列は、データを要約し、データセット内のさまざまな変数間の関係を全体的に分析するのに非常に役立ちます。