確率関数

によるベンジャミン・アンダーソン博士 8月 5, 2023 確率 0コメント

この記事では、確率関数とは何かについて説明します。このようにして、確率関数の意味、その性質、および確率関数の計算の具体例がわかります。さらに、確率関数と他のタイプの確率関数の違いも示します。

確率関数とは何ですか?

確率関数は、確率質量関数とも呼ばれ、離散確率変数が特定の値を取る確率を記述する数学関数です。

つまり、確率関数は、値に正確に等しい離散変数に関連付けられた確率を返します。

$f(x)=P[X=x]$

たとえば、サイコロを振るときに任意の数字が出る確率は 1/6 (サイコロには 6 面がある) であるため、このサンプル空間に関連付けられた確率関数は、n の値に関係なく 1/6 に等しくなります。

確率関数には次の特性があります。

$f(x)\geq 0$

$f(x)\leq 1$

$\displaystyle \sum_{i=1}^{+\infty}f(x_i)=\sum_{i=1}^{+\infty}p_i=1$

確率関数の定義と特徴を理解したところで、このタイプの確率関数の例を見てみましょう。

まず第一に、表が出る確率を計算する必要があります。これを行うには、考えられるケースをケースの総数で割る必要があります。次の表で、すべての確率の計算を確認できます。

すべての確率を計算したら、確率関数の値をグラフで表すことができます。

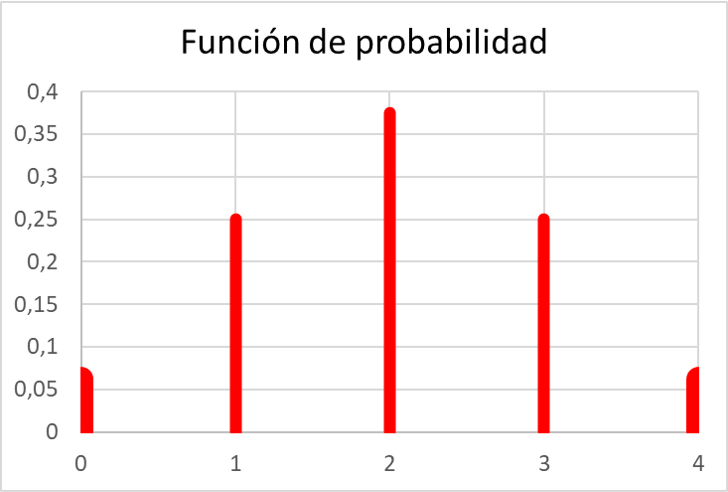
ご覧のとおり、演習の確率関数は、すべての値が 0 と 1 の間にあり、さらに、すべての値の合計が 1 に等しいため、確率関数のすべての特性を満たしています。

このセクションでは、確率関数と密度関数の違いについて説明します。これらは同じ目的を持つ 2 種類の確率関数ですが、使用されるケースが異なるためです。

確率関数と密度関数の違いは、確率が表す変数のタイプです。確率関数は離散変数の確率を定義するために使用され、密度関数は連続変数の確率を定義するために使用されます。

したがって、変数に応じて、確率関数または密度関数が使用されます。

密度関数の詳細については、次のリンクをクリックしてください。

確率関数と分布関数の違いは、定義される確率のタイプです。確率関数は変数が特定の値を取る確率を示し、分布関数は変数の累積確率を表します。

したがって、分布関数は確率関数から計算されます。

例として、次のリンクでは、上記の演習で見つかった確率関数に基づいて、4 回のコイントスで表を得る分布関数の計算を確認できます。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る