箱ひげ図を使用する必要があるのはどのような場合ですか? (3つのシナリオ)

によるベンジャミン・アンダーソン博士 7月 23, 2023 ガイド 0コメント

箱ひげ図は、データセットの 5 桁の概要を表示するプロットの一種で、次のものが含まれます。

3 つの簡単な手順を使用して、任意のデータセットの箱ひげ図を作成します。

通常、次の 3 つのシナリオのいずれかで箱ひげ図を作成します。

シナリオ 1: データセット内の値の分布を視覚化します。

箱ひげ図を使用すると、データセット内の値の分布をすばやく視覚化し、5 つの数値要約値がどこにあるかを確認できます。

シナリオ 2: 2 つ以上のディストリビューションを比較します。

並べた箱ひげ図を使用すると、2 つ以上の分布間の差異を視覚化し、分布間の中央値と値の分布を比較できます。

シナリオ 3: 外れ値を特定するため。

箱ひげ図では、外れ値は通常、各ひげを超えて広がる小さな円で表されます。観測値が次の基準のいずれかを満たす場合、その観測値は外れ値として定義されます。

箱ひげ図を作成すると、分布に外れ値があるかどうかをすぐに確認できます。

次の例は、各シナリオで箱ひげ図を使用する方法を示しています。

バスケットボールのコーチが、チームの選手が獲得したポイントの分布を視覚化したいと考え、次の箱ひげ図を作成するとします。

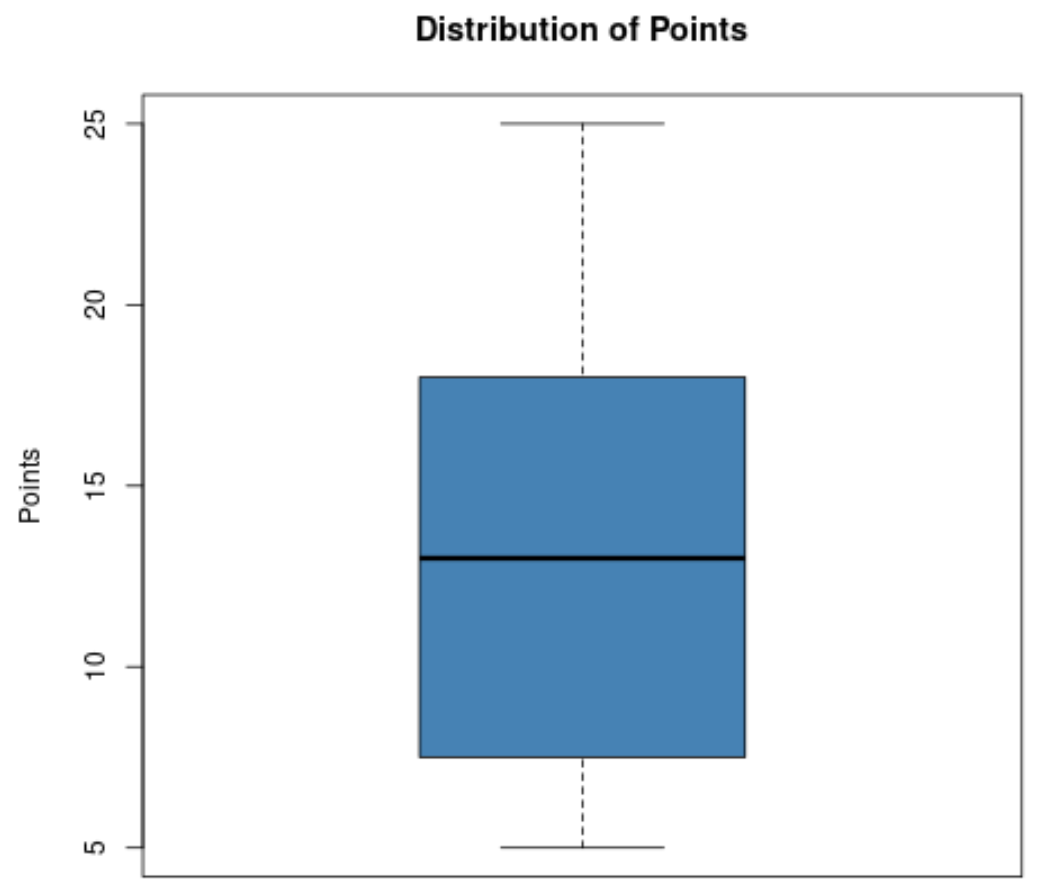
この箱ひげ図に基づいて、次の値をすぐに確認できます。

これにより、コーチは、プレーヤーが獲得したポイントが 5 ～ 25 の範囲であること、獲得ポイントの中央値が約 13 であること、およびプレーヤーの 50% が 1 試合あたり約 8 ～ 18 ポイントを獲得していることをすぐに確認できます。

スポーツアナリストが 3 つの異なるチームのバスケットボール選手の得点分布を比較し、次の箱ひげ図を作成するとします。

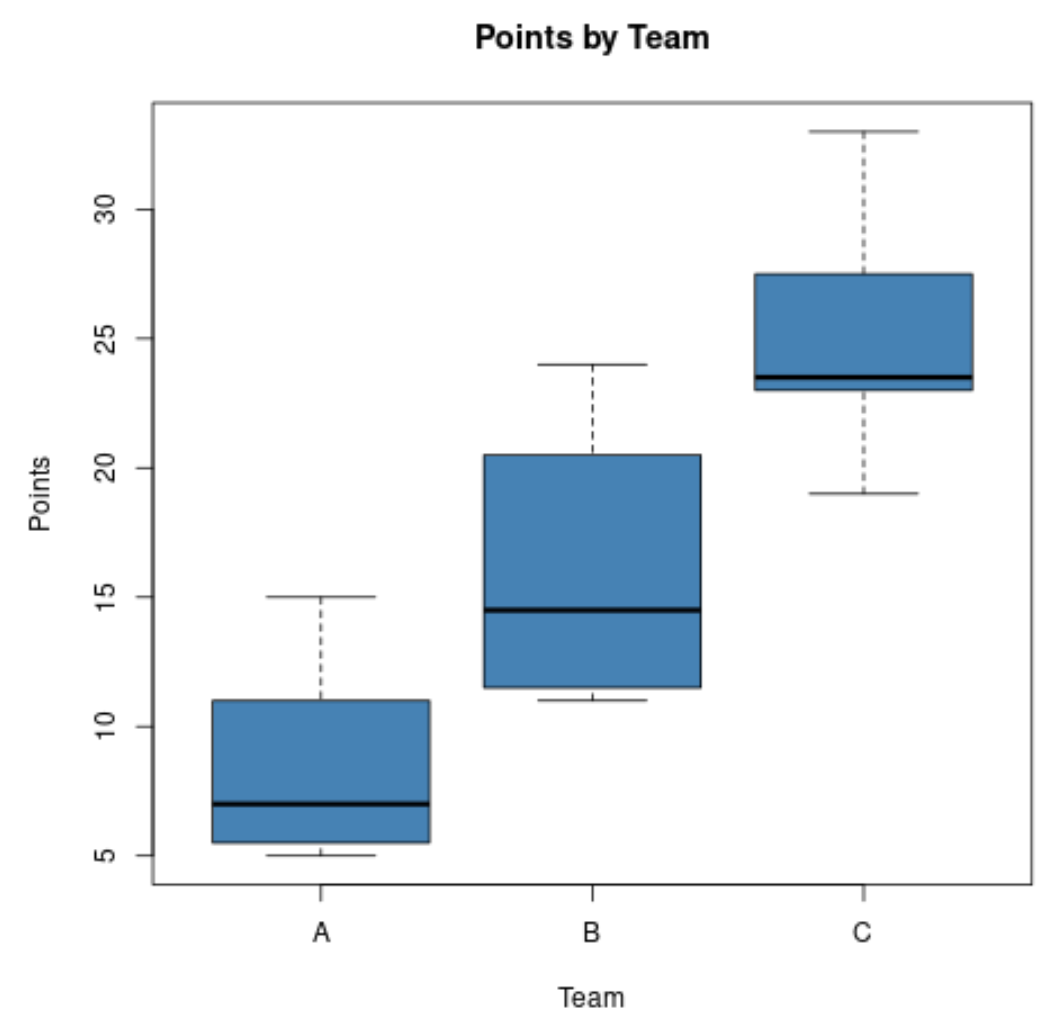
これらのグラフを使用すると、チーム C の中間点のスコアが最も高く、チーム A の中間点のスコアが最も低いことがすぐにわかります。

また、チーム B の箱ひげ図が最も長い箱を持っているため、チーム B が得点の分布が最も大きいこともすぐにわかります。

バスケットボールのコーチが、自分の選手の 1 人が得点の点で外れ値であるかどうかを知りたいとします。彼は、プレーヤーが獲得したポイントの分布を視覚化するために、次の箱ひげ図を作成することにしました。

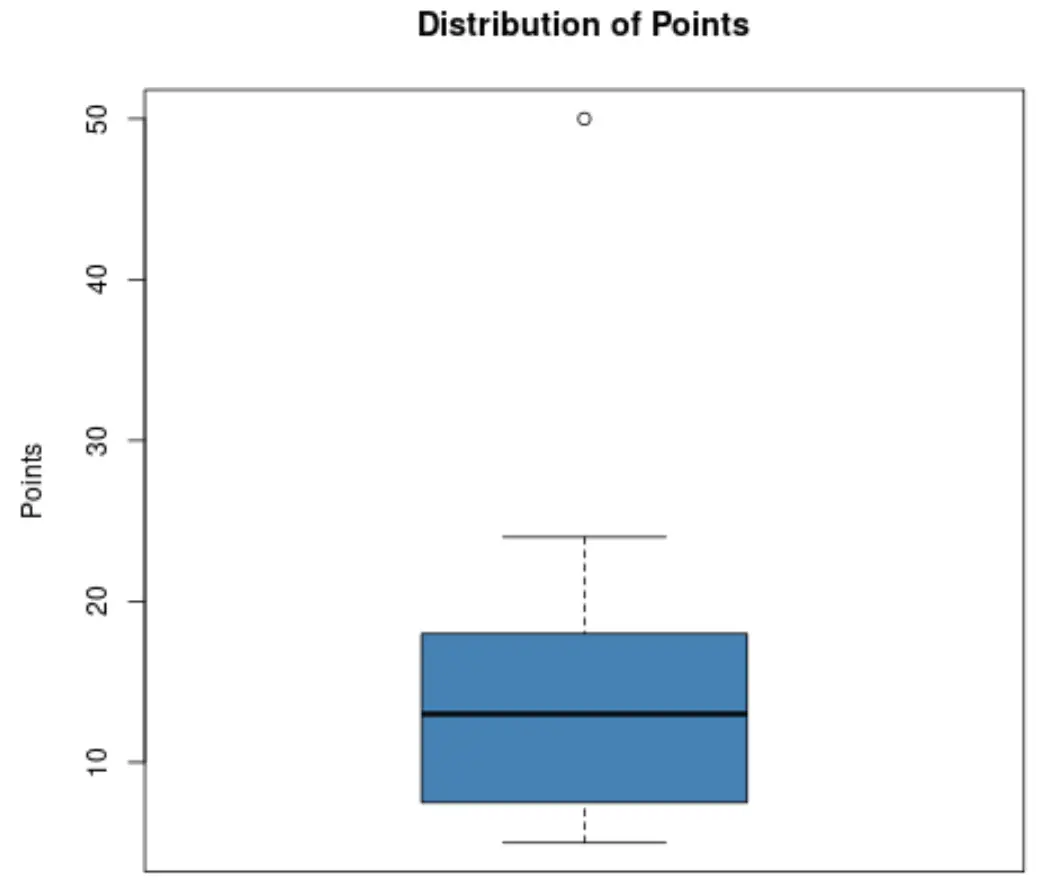
このプロットを使用すると、コーチはプロットの上部にある小さな点が外れ値を示していることがわかります。

具体的には、プレーヤーの 1 人が約 50 得点を獲得しましたが、これは他のすべての得点と比較して異常値であると考えられます。

次のチュートリアルでは、実際に箱ひげ図を使用する方法について詳しく説明します。

次のチュートリアルでは、さまざまな統計ソフトウェアで箱ひげ図を作成する方法を説明します。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る