箱ひげ図
この記事では、箱ひげ図 (箱ひげ図 (または箱ひげ図) とも呼ばれる) とは何かについて説明します。これらのタイプの統計図がどのように作成されるか、箱ひげ図とその解釈の演習を解決することができます。
箱ひげ図とは何ですか?
箱ひげ図 は、箱ひげ図または箱ひげ図とも呼ばれ、四分位数を使用して一連の統計データを視覚的に表すグラフです。
箱ひげ図の主な特徴は、データの四分位数、中央値、極値、外れ値を示すため、一連のデータの分散を迅速に視覚化できることです。
したがって、このタイプの図は、長方形のボックスと、次の値が現れる数本の線 (またはひげ) で構成されます。
- ボックスの境界は、第 1 四分位数と第 3 四分位数(Q 1および Q 3 ) を示します。ボックス内の垂直線は中央値(第 2 四分位Q2に相当) です。
- ひげ (または腕) の限界は極値、つまりデータ系列の最小値と最大値です。
- ひげの外側の点は外れ値、つまり、おそらく誤って測定されたデータであり、したがって統計的研究では考慮すべきではありません。
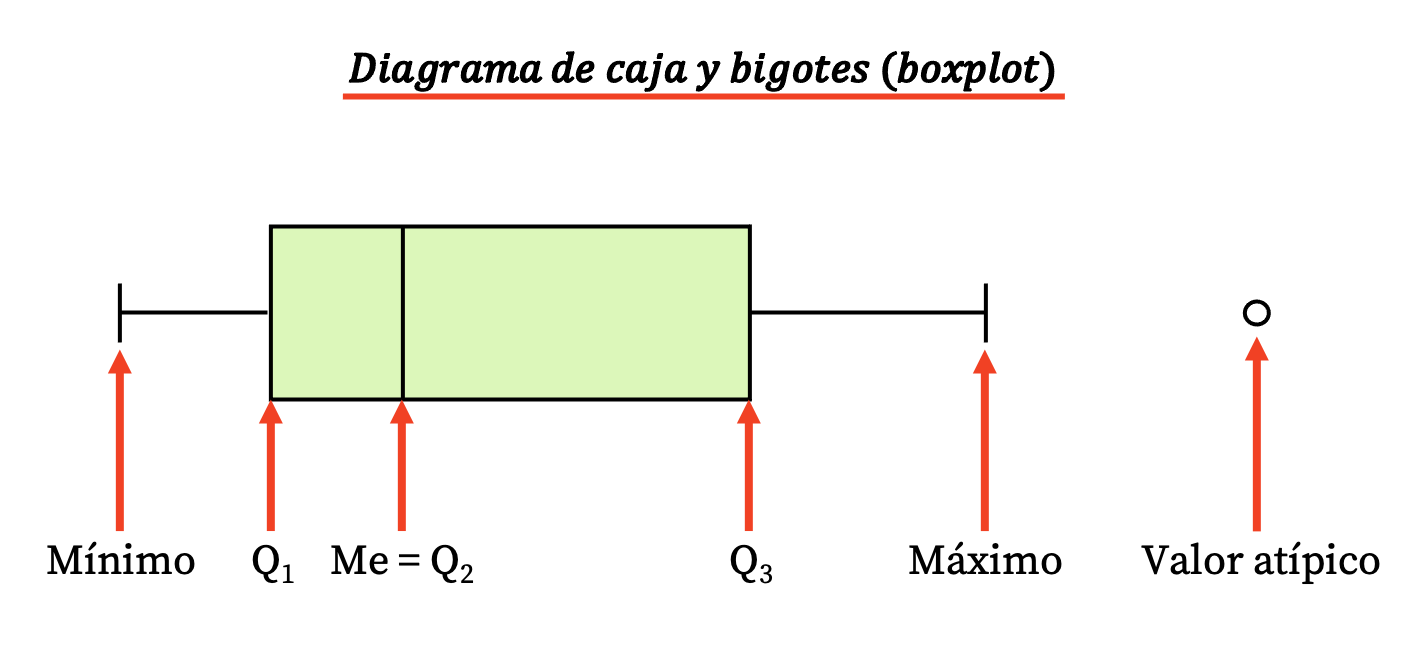
第 3 四分位数と第 1 四分位数の差は、統計的分散のもう 1 つの尺度である四分位間範囲 (または四分位間範囲) であることに注意してください。
箱ひげ図は、数値変数を比較するのに非常に役立ちます。ただし、カテゴリ変数を表すには適していません。
箱ひげ図を作成する方法
データ系列から箱ひげ図 (または箱ひげ図) を作成するには、次の手順を実行する必要があります。
- 統計データの例を整理します。
- 四分位数 (Q 1 、Q 2 、Q 3 ) を計算し、図のボックスとして表します。第 1 四分位数と第 3 四分位数はボックスの限界に対応し、中央値 (第 2 四分位数) を表すには、値が配置されているボックス内の線を引く必要があります。
- 四分位範囲を計算します。これは、第 3 四分位から第 1 四分位を引いた値に等しくなります。
- 許容値 LI と LS を計算します。その式は次のとおりです。
- LI 未満または LS より大きい値であるサンプル外れ値を特定します。ひげの範囲外のこれらの値はドットで表します。
- LI と LS によって形成される区間内の最小値と最大値である極値を特定して表します。これらの値は、図の 2 つのひげの端を表します。
![]()
![]()
![]()
箱ひげ図の例
箱ひげ図 (または箱ひげ図) の定義と理論を考慮して、概念をよりよく理解し、このタイプの統計プロットがどのように実行されるかを確認するための具体的な例を以下に示します。
- 次の統計データセットの箱ひげ図を描きます。

この場合、データはすでに最小値から最大値の順に並べられているため、変更する必要はありません。それ以外の場合は、最初にサンプル データを並べ替える必要があります。
次に、サンプルの四分位を抽出します。
![]()
![]()
![]()
3 つの四分位を計算したら、四分位 3 から四分位 1 を減算して四分位間の範囲を求めます。
![]()
次に、データが異常であるとみなされる値である LI および LS 制限を計算します。これを行うには、次の式を使用する必要があります。
![]()
![]()
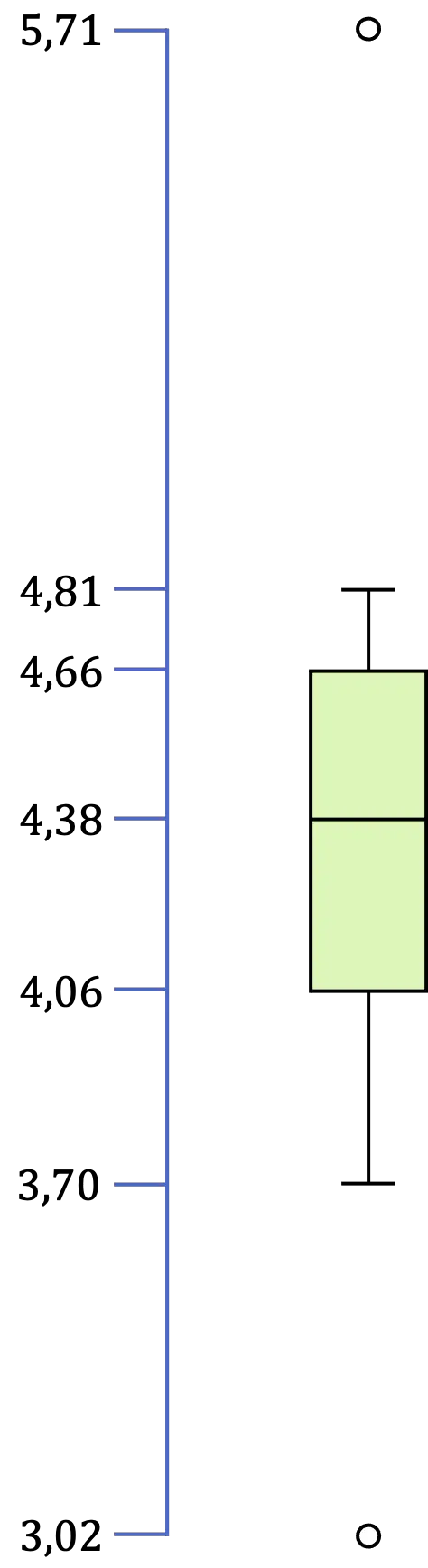
この場合、3.02 は 3.16 より小さく、5.71 は 5.56 より大きいため、外れ値が 2 つあります。
![]()
最後に、区間 [LI,LS] 内にあるすべてのデータの最小値と最大値である極値を特定する作業が残ります。したがって、この例では、最小値は 3.70、最大値は 4.81 になります。
![]()
![]()
したがって、ボックスとウィスカー プロットのすべての値を特定したら、あとはグラフィック表現を作成するだけです。
箱ひげ図は何に使用されますか?
最後に、箱ひげ図 (または箱ひげ図) の目的と解釈方法を見てみましょう。
明らかに、箱ひげ図は、データ系列の四分位数、四分位間範囲、中央値、極値、外れ値をすばやく知るのに非常に役立ちます。これらの統計的尺度はすべて簡単に確認できるためです。
さらに、箱ひげ図はデータセット全体を視覚的に表すため、統計サンプルの対称性を分析するために使用されます。中央値がボックスの中心にない場合は、サンプルが対称ではないことを意味します。
同様に、箱ひげ図は短期間での最大値、最小値、中間値を確認できるため、一定期間にわたる株価の変動を表すために株式市場で広く使用されています。時間を節約し、より迅速な意思決定を行うことができます。