累積周波数ポリゴン
この記事では、累積頻度ポリゴンとは何かについて説明します。したがって、累積頻度多角形の定義、累積頻度多角形の作成方法、およびこのタイプの統計グラフの特徴がわかります。
説明を始める前に、累積頻度ポリゴンが何で構成され、どのように構築されるかをよりよく理解するために、次の投稿を参照することをお勧めします。
➤参照:周波数ポリゴンとは何ですか?
累積頻度ポリゴンとは何ですか?
累積度数ポリゴンは、データセットの累積度数が点で表され、線で接続された統計グラフの一種です。言い換えれば、累積度数ポリゴンは、統計サンプルの累積度数をグラフで表現したものです。
したがって、累積頻度ポリゴンは、特定の値以下のデータの数を決定するために使用されます。
論理的には、累積度数ポリゴンの概念を理解するには、統計における累積度数の意味を明確にする必要があるため、説明を続ける前に次の記事を確認することをお勧めします。
➤ 「累積頻度とは何ですか?」を参照してください。
累積周波数ポリゴンを作成する方法
累積頻度ポリゴンを表すには、次の手順に従う必要があります。
- 累積周波数ポリゴンを表す統計データを収集します。
- 値を最小値から最大値の順に並べた度数表を作成します。
- データセットの累積頻度を計算します。
- 累積頻度をグラフ上の点としてプロットします。
- グラフ上の連続する点を線で結合して、累積頻度多角形を形成します。
累積頻度ポリゴンの例
累積頻度ポリゴンがどのように作成されるかを理解できるように、具体的な例を次に示します。
- 50 人のサンプル サイズが測定され、データは次の度数表に記録されました。累積頻度ポリゴンを使用してデータをグラフ化します。
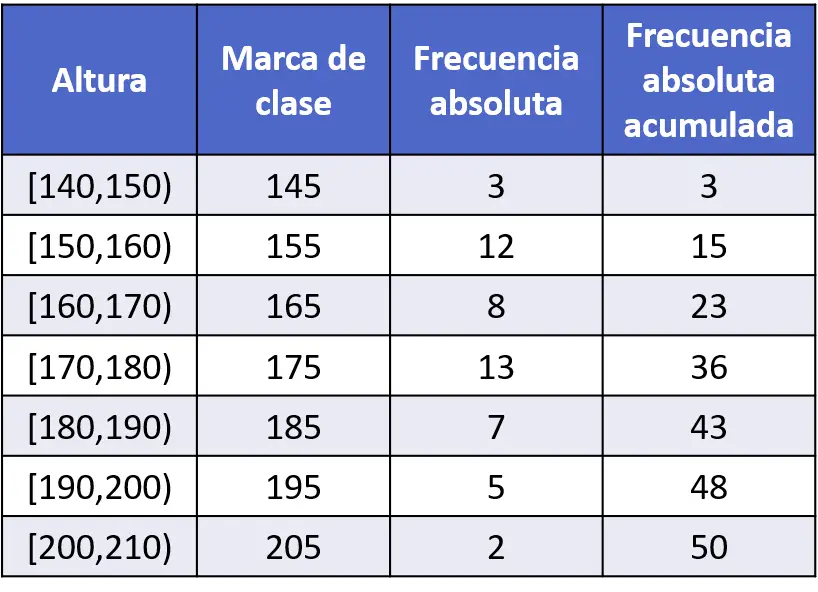
この場合、累積絶対周波数はすでに計算されていますが、計算方法がわからない場合は、次のリンクをクリックすると説明が表示されます。
➤参照:累積絶対頻度の計算方法
そして、累積絶対頻度がわかったら、累積頻度の多角形を表すには、グラフ上の点の形で値を表し、それらを実線で結ぶだけで十分です。
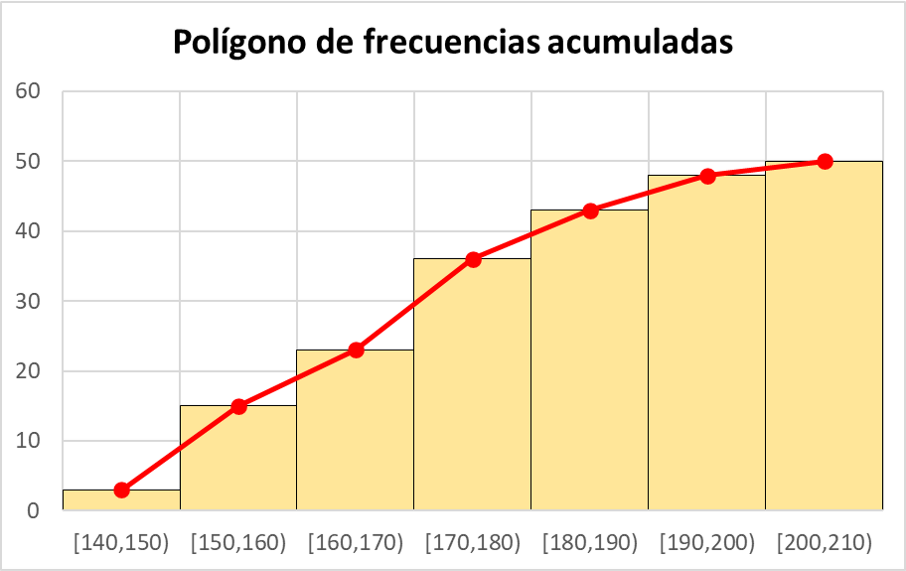
累積頻度多角形は、累積頻度ヒストグラムのバーの中点を結合することによっても取得できることに注意してください。
累積頻度ポリゴンの特徴
累積周波数ポリゴンの特性は次のとおりです。
- 累積された絶対度数が累積度数多角形で表現される場合、終点は常にデータの総数になります。
- ただし、累積相対度数をグラフにプロットすると、終点は常に 1 になります。
- 累積頻度ポリゴンで表現できるのは量的変数のみです。このタイプの統計図は、質的変数には役に立ちません。
- 累積頻度ポリゴンを使用すると、特定の値を下回るデータ ポイントの数を視覚的に知ることができます。