ファッション（統計）

によるベンジャミン・アンダーソン博士 8月 5, 2023 統計 0コメント

この記事では、統計におけるモードについて説明します。グループ化されたデータとグループ化されていないデータの統計モードを見つける方法、さまざまなタイプのモード、およびこの統計的尺度のいくつかの例を学習します。

統計における最頻値とは何ですか?

統計において、最頻値はデータセット内で最も高い絶対頻度を持つ値、つまり、最頻値はデータセット内で最も繰り返される値です。

したがって、統計データセットの最頻値を計算するには、サンプル内で各データ要素が出現する回数を数えるだけで、最も多く繰り返されたデータが最頻値となります。

通常、最も繰り返される値が分布の中心にあるため、モードは統計分布を定義するために使用されます。

モードは、統計モードまたは最頻値とも言えます。同様に、データが間隔にグループ化される場合、最も繰り返される間隔がモーダル間隔またはモーダルクラスになります。

一般に、 Moという用語は統計モードの記号として使用されます。たとえば、分布モード X は Mo(X) です。

最頻値は中心位置、中央値、平均値の統計的尺度であることに留意してください。以下では、これらの統計的尺度がそれぞれ何を意味するのかを見ていきます。

統計におけるモードの種類

統計では、最も繰り返される値の数に応じて分類されるいくつかのタイプのモードがあります。

ユニモーダルモード: 最大繰り返し回数を持つ値は 1 つだけです。たとえば、[1、4、2、4、5、3]。
バイモーダルモード: 最大繰り返し回数は 2 つの異なる値で発生し、両方の値が同じ回数繰り返されます。たとえば、[2、6、7、2、3、6、9]。
マルチモーダルモード: 3 つ以上の値が同じ最大繰り返し回数を持ちます。たとえば、[3、3、4、1、3、4、2、1、4、5、2、1]。

統計モードの見つけ方

データセットの統計モードを見つけるには、次の手順に従う必要があります。

データを整理します。この手順は必須ではありませんが、数を数えるのが簡単になります。
各数字が何回出現するかを数えます。
最も頻繁に表示される数字は統計モードです。

統計モードの例

統計におけるファッションの定義を考慮して、概念をよりよく理解できるように、以下に各タイプのファッションの例を示します。

ユニモーダルモードの例

次のデータセットのモードは何ですか?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

番号は順序付けされていないため、モードを見つけやすくするために最初に番号を付けます。

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

2 と 9 という数字は 2 回現れますが、5 という数字は 3 回繰り返されます。したがって、データ系列の最頻値は 5 です。

$Mo=5$

バイモーダルモードの例

次のデータセットのモードを計算します。

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

まず数字を順番に並べます。

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

ご覧のとおり、数字の 6 と数字 8 は合計 4 回表示され、これが最大の繰り返し回数です。したがって、この場合は二峰性モードであり、2 つの数値がデータセットのモードになります。

$Mo=\{ 6 \ ; \ 8\}$

マルチモーダルモードの例

次のデータセットモードを見つけます。

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

データが多いため、カウントしやすくするために、まず昇順に並べ替えます。

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

最も多く繰り返される数字は 20、27、および 31 で、3 つの数字はすべて 5 回繰り返されます。したがって、この例のモードはマルチモーダルです。

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

ファッション電卓

統計サンプルのデータを次のオンライン計算機に入力して、その最頻値を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

グループ化されたデータのモード

データが間隔の形式でグループ化されている場合、各データが何回繰り返されるかは実際にはわかりません。わかるのは各間隔の頻度だけです。

したがって、間隔にグループ化されたデータのモードを計算するには、次の式を使用する必要があります。

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

金：

Ｌ _ｉは、モーダル間隔（最高絶対周波数間隔）の下限である。
f _iはモーダル区間の絶対周波数です。
f _i-1は、モーダルの前の区間の絶対周波数です。
f _i+1はモーダル後の区間の絶対周波数です。
A _iはモーダル区間の幅です。

例として、以下では、間隔にグループ化されたデータのモードを計算する演習を解決しました。

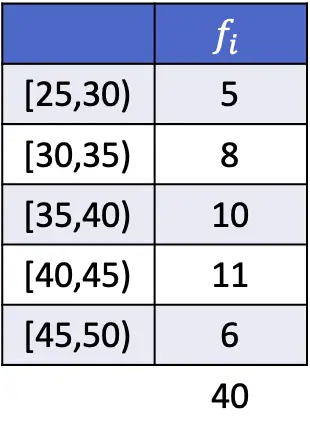
この場合、絶対周波数が最大の区間であるため、モーダル区間は [40,45) になります。したがって、グループ化されたデータのモード式パラメータは次のとおりです。

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

したがって、式を適用して間隔にグループ化されたデータのモードを決定し、計算を実行します。

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

最頻値、平均値、中央値の違い

この最後のセクションでは、最頻値、平均値、中央値の違いを見ていきます。 3 つはすべて中心位置の統計的尺度であるため、意味が異なります。

記事全体で説明したように、数学におけるモードは、データセット内で最も繰り返される値です。

次に、平均値はすべての統計データの平均値です。したがって、特定のデータの平均を取得するには、すべてのデータを加算し、その結果を観測値の数で割る必要があります。

最後に、中央値は、データが順序付けされたときに中心の位置を占める値です。

したがって、3 つの統計的尺度は、確率分布の中心値のアイデアを提供するため、確率分布を定義するのに役立ちます。ただし、ある尺度が他の尺度より優れているというわけではなく、意味する概念が異なるだけであることに留意してください。

ファッション特性

ファッションのプロパティは次のとおりです。

最頻値は量的変数と質的変数の両方に見られます。
確率変数に線形変換を適用すると、適用された演算に応じて平均値が変化します。

$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$

一般に、このモードは外れ値の影響を受けません。
すべての値が同じ周波数を持つ場合、モードはありません。

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る