Ti-84 電卓で線形回帰を実行する方法

線形回帰は、説明変数 x と応答変数 y の関係を理解するために使用できる方法です。

このチュートリアルでは、TI-84 電卓で線形回帰を実行する方法を説明します。

例: TI-84 電卓での線形回帰

学生の試験勉強時間と試験で得た成績の関係を理解したいとします。

この関係を調査するには、TI-84 計算機で次の手順を実行し、学習時間を説明変数として、試験の成績を応答変数として使用して単純な線形回帰を実行します。

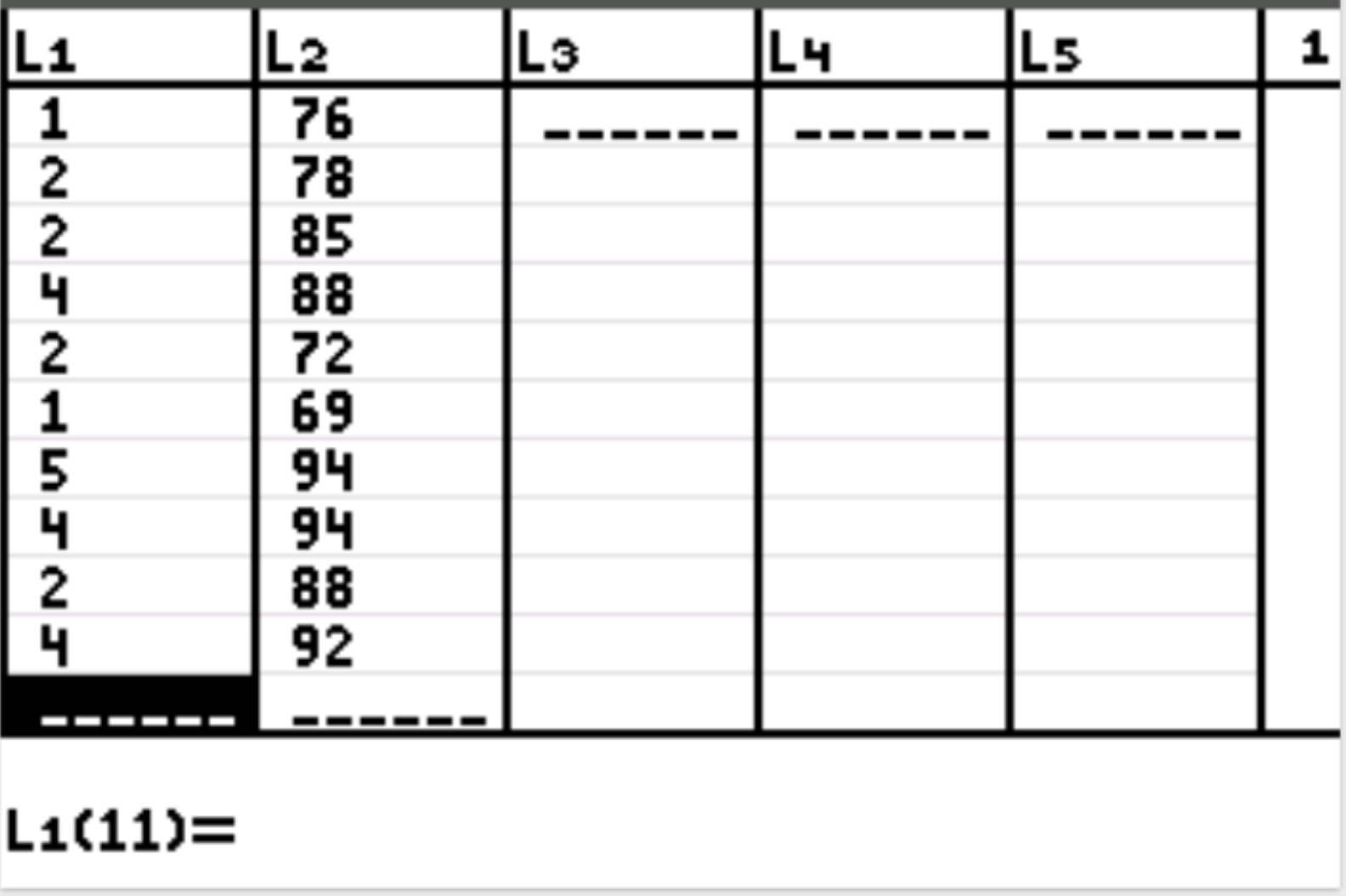
ステップ 1: データを入力します。

まずは説明変数と応答変数のデータ値を入力します。 Statを押してからEDITを押します。 L1 列に説明変数 (学習時間) の次の値を入力し、L2 列に応答変数 (試験のスコア) の値を入力します。

ステップ 2: 線形回帰を実行します。

次に、線形回帰を実行します。 「Stat」を押してから「CALC」までスクロールします。次に、 「8: Linreg(a+bx)」までスクロールし、 Enterを押します。

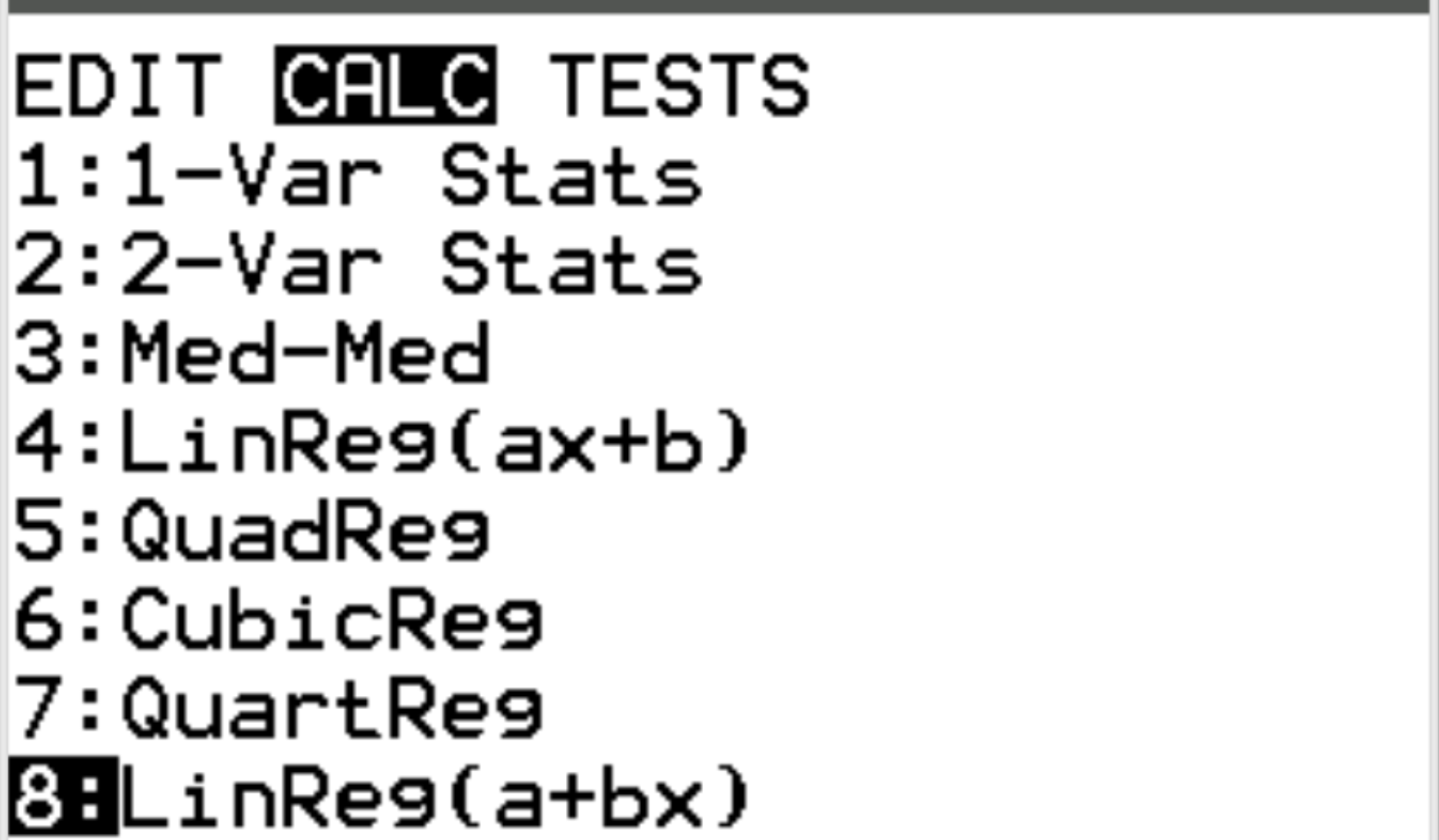
Xlist と Ylist については、データの入力に使用した列である L1 と L2 が選択されていることを確認してください。 FreqList は空のままにしておきます。 「計算」まで下にスクロールし、 Enterを押します。次の出力が自動的に表示されます。

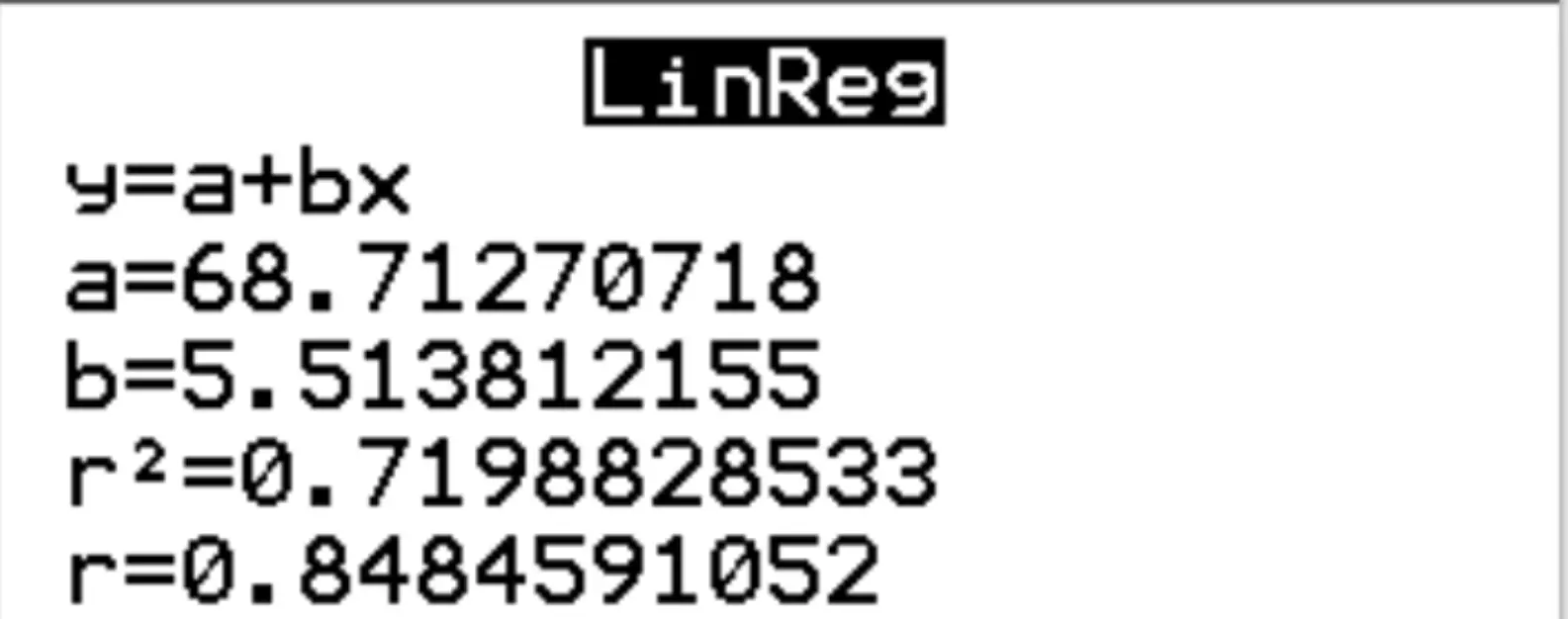
ステップ 3: 結果を解釈します。

結果から、推定された回帰式は次のとおりであることがわかります。

試験スコア = 68.7127 + 5.5138*(時間)

時間係数は、学習時間が追加されるごとに、試験のスコアが平均5.5138増加することを意味すると解釈します。切片の係数は、勉強時間が 0 時間の学生の予想される試験スコアが68.7127であることを意味すると解釈します。

この推定回帰式を使用して、学習時間数に基づいて生徒の予想される試験スコアを計算できます。

たとえば、3 時間勉強した生徒は、試験スコア85.25を達成する必要があります。

試験のスコア = 68.7127 + 5.5138*(3) = 85.25

回帰モデルの r の二乗が r ² = 0.7199であることもわかります。

この値は決定係数として知られています。説明変数によって説明できる応答変数の分散の割合です。この例では、試験得点の変動の 71.99% は勉強時間数で説明できます。

追加リソース

TI-84 電卓で残差プロットを作成する方法
TI-84 電卓で二次回帰を実行する方法
TI-84 電卓で指数回帰を実行する方法
TI-84 電卓で対数回帰を実行する方法