記述統計と推論統計: 違いは何ですか?

統計の分野には 2 つの主要な分野があります。

• 記述統計
• 推論統計

このチュートリアルでは、2 つのブランチの違いと、特定の状況でそれぞれが役立つ理由について説明します。

記述統計

一言で言えば、記述統計は、要約統計、グラフ、表を使用して一連の生データを説明することを目的としています。

記述統計は、単に生のデータ値を何行も見るよりも、データのグループをはるかに迅速かつ簡単に理解できるため便利です。

たとえば、特定の学校の 1,000 人の生徒のテストのスコアを示す生データ セットがあるとします。テストのスコアの分布だけでなく、テストの平均スコアにも興味があるかもしれません。

記述統計を使用すると、平均スコアを見つけて、スコアの分布を視覚化するのに役立つグラフを作成できます。

これにより、生データを見るだけよりもはるかに簡単に生徒のテストのスコアを理解できるようになります。

記述統計の一般的な形式

記述統計には 3 つの一般的な形式があります。

1. 要約統計。これらは、単一の数値を使用してデータを要約した統計です。要約統計量には一般的に 2 つのタイプがあります。

• 中心傾向の測定:これらの数値は、データセットの中心がどこにあるかを示します。例としては、平均的なものが挙げられます。  と中央値。
• 分散の尺度:これらの数値は、データセット内の値の分布を表します。例には、間隔、四分位範囲、標準偏差、分散などがあります。

2.グラフィックス。グラフはデータを視覚化するのに役立ちます。データの視覚化に使用される一般的な種類のグラフには、 箱ひげ図、 ヒストグラム、 幹葉図、 散布図などがあります。

3. テーブル。テーブルは、データがどのように分散されているかを理解するのに役立ちます。一般的なタイプのテーブルは度数テーブルで、特定の範囲内にデータ値がいくつあるかを示します。

記述統計の使用例

次の例は、現実世界で記述統計を使用する方法を示しています。

ある学校の 1,000 人の生徒全員が同じテストを受けると仮定します。テスト結果の分布を理解したいので、次の記述統計を使用します。

1. 概要統計

平均: 82.13 。これは、1,000 人の生徒のテストの平均点が 82.13 であることを示しています。

中央値: 84。これは、全生徒の半分が 84 以上のスコアを持ち、残りの半分が 84 未満のスコアを持っていることを示しています。

最大: 100。最小: 45。これは、生徒が取得した最大スコアが 100 で、最小スコアが 45 であることを示します。最大値と最小値の差を示す範囲は 55 です。

2.グラフィックス

テスト結果の分布を視覚化するには、ヒストグラム (長方形の棒を使用して頻度を表すグラフの一種) を作成します。

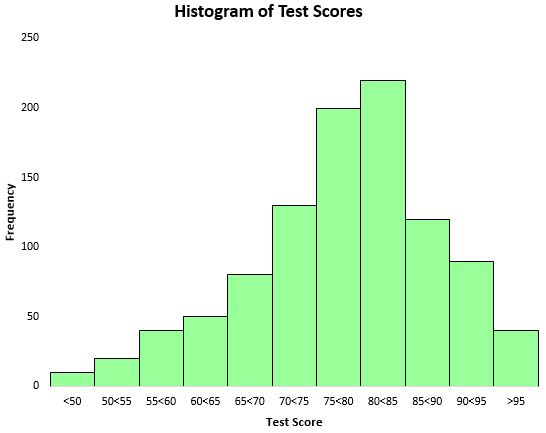
このヒストグラムに基づいて、テストのスコアの分布がほぼ釣鐘型であることがわかります。ほとんどの学生のスコアは 70 ～ 90 でしたが、95 を超えるスコアはほとんどなく、50 未満のスコアはさらに少数でした。

3. テーブル

スコアの分布を理解するもう 1 つの簡単な方法は、頻度表を作成することです。たとえば、次の度数表は、さまざまな範囲で得点した生徒の割合を示しています。

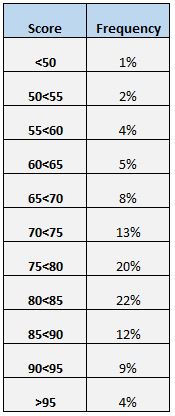
95 点以上のスコアを獲得した生徒は全体の 4% のみであることがわかります。また、(12% + 9% + 4% = ) 全生徒の 25% が 85 以上のスコアを獲得したこともわかります。

度数表は、データ値の何パーセントが特定の値を上回るか下回るかを知りたい場合に特に便利です。たとえば、学校が 75 点を超えるスコアを「許容できる」テストスコアとみなしているとします。

度数表を見ると、(20% + 22% + 12% + 9% + 4% = ) 67% の学生がテストで合格点を獲得したことが簡単にわかります。

推論統計

一言で言えば、推論統計では、少数のデータサンプルを使用して、サンプルが抽出されたより大きな母集団についての結論を導き出します。

たとえば、ある国の何百万人もの人々の政治的好みを理解したいと思うかもしれません。

しかし、国内のすべての個人を調査するには時間と費用がかかりすぎます。そこで、代わりに、たとえば 1,000 人のアメリカ人を対象とした小規模な調査を実施し、その調査結果を使用して人口全体についての結論を導き出します。

これが推論統計の前提全体です。つまり、母集団に関する質問に答えたいので、その母集団の小さなサンプルのデータを取得し、そのサンプル データを使用して母集団に関する推論を導き出します。

代表的なサンプルの重要性

サンプルを使用して母集団に関する結論を導き出す能力に自信を持ってするには、 代表的なサンプル、つまり母集団内の個人の特徴がサンプルとよく一致するサンプルがあることを確認する必要があります。特徴。人口全体の。

理想的には、サンプルは母集団の「ミニバージョン」に似ていることが望ましいです。したがって、50% が女子、50% が男子で構成される生徒の母集団について結論を導き出したい場合、90% が男子で 10% のみが女子を含むサンプルは代表的ではありません。

サンプルが母集団全体と類似していない場合、サンプルからの結果を母集団全体に自信を持って一般化することはできません。

代表サンプルの入手方法

代表的なサンプルを入手できる可能性を最大限に高めるには、次の 2 つの点に焦点を当てる必要があります。

1. 必ずランダムなサンプリング方法を使用してください。

代表的なサンプルを生成するために使用できる、次のようなランダムサンプリング方法がいくつかあります。

• 単純なランダムサンプル
• 体系的なランダムサンプル
• クラスターのランダムサンプル
• 層別ランダムサンプル

ランダムサンプリング方法では、母集団の各メンバーがサンプルに含まれる確率が等しいため、代表的なサンプルが生成される傾向があります。

2. サンプルサイズが十分に大きいことを確認してください。

適切なサンプリング方法を使用することに加えて、サンプルが十分な大きさであることを確認して、より大きな母集団に一般化できる十分なデータを確保することが重要です。

サンプル サイズを決定するには、調査対象の母集団のサイズ、使用する信頼水準、および許容できると考えられる誤差の範囲を考慮する必要があります。

幸いなことに、オンライン計算機を使用してこれらの値を入力し、サンプル サイズをどの程度にすべきかを確認できます。

推論統計の一般的な形式

推論統計には 3 つの一般的な形式があります。

1. 仮説検証。

私たちは多くの場合、次のような母集団に関する質問に答えたいと考えます。

• オハイオ州で候補者 A を支持する人の割合は 50% を超えていますか?
• 特定の植物の平均高さは 14 インチに相当しますか?
• A学校とB学校の生徒の平均身長に違いはありますか?

これらの質問に答えるために、仮説検定を実行することができます。これにより、サンプルからのデータを使用して母集団に関する結論を導き出すことができます。

2. 信頼区間。

場合によっては、母集団の特定の値を推定したいことがあります。たとえば、オーストラリアの特定の植物種の平均高さに興味があるとします。

国内のすべての植物を歩き回って測定する代わりに、少量の植物サンプルを集めてそれぞれを測定することができます。次に、サンプル内の植物の平均高さを使用して、母集団の平均高さを推定できます。

ただし、私たちのサンプルが完全な母集団推定値を提供する可能性は低いです。幸いなことに、この不確実性は信頼区間を作成することで説明できます。これは、真の母集団パラメータがその範囲内にあると確信できる値の範囲を提供します。

たとえば、95% 信頼区間 [13.2, 14.8] を生成できます。これは、この植物種の真の平均高さが 13.2 インチから 14.8 インチの間にあることを 95% 確信していることを意味します。

3. 回帰。

場合によっては、母集団内の 2 つの変数間の関係を理解したいことがあります。

たとえば、 1 週間あたりの勉強時間とテストのスコアが関連しているかどうかを知りたいとします。この質問に答えるには、回帰分析として知られる手法を実行できます。

したがって、100 人の学生の学習時間数とテストの得点を調べ、回帰分析を実行して、2 つの変数間に有意な関係があるかどうかを確認できます。

回帰の p 値が有意であることが判明した場合、学生母集団全体におけるこれら 2 つの変数の間に有意な関係があると結論付けることができます。

記述統計と推論統計の違い

要約すると、記述統計と推論統計の違いは次のように説明できます。

記述統計では、概要統計、グラフ、表を使用して一連のデータを説明します。

これは、個々のデータ値をすべて調べることなく、一連のデータを迅速かつ簡単に理解するのに役立ちます。

推論統計では、サンプルを使用して、より大きな母集団についての結論を導き出します。

母集団について答えたい質問に応じて、仮説検定、信頼区間、回帰分析のいずれかの方法を使用することを決定できます。

これらの方法のいずれかを使用する場合は、 サンプルが母集団を代表するものでなければならないことに留意してください。そうしないと、導き出される結論は信頼できなくなります。