負の二項分布

によるベンジャミン・アンダーソン博士 8月 3, 2023 確率 0コメント

この記事では、負の二項分布とは何か、またそれが何に使用されるのかについて説明します。また、負の二項分布の公式、具体例、およびこのタイプの確率分布の特性についても説明します。最後に、オンライン計算機を使用して負の二項分布確率を計算できるようになります。

負の二項分布とは何ですか?

負の二項分布は、指定された数の肯定的な結果を得るために必要なベルヌーイ試行回数を表す確率分布です。

したがって、負の二項分布には 2 つの特徴的なパラメーターがあります。rは望ましい成功結果の数、 pは実行された各ベルヌーイ実験の成功確率です。

$X\sim \text{BN}(r,p)$

ベルヌーイテストは、「成功」と「失敗」という 2 つの結果が考えられる実験であることに注意してください。したがって、「成功」の確率がpの場合、「失敗」の確率はq=1-pです。

したがって、負の二項分布は、正の結果を得るために必要な数のベルヌーイ試行が実行されるプロセスを定義します。さらに、これらのベルヌーイ試行はすべて独立しており、成功の確率は一定です。

たとえば、負の二項分布に従う確率変数は、数字の 6 が 3 回振られるまでにサイコロを振らなければならない回数です。

負の二項分布と二項分布の違いは、負の二項分布は特定の数の成功結果を得るまでにかかる回数をカウントするのに対し、二項分布は一連のベルヌーイテストにおける成功ケースの数をカウントすることです。

➤参照:二項分布とは何ですか?

負の二項分布式

パラメーターr、p、x が与えられると、負の二項分布の確率は、 xr内のx-1の組み合わせ数と(1-p) ^xrとp ^rを乗算することによって計算されます。

したがって、負の二項分布確率を計算する式は次のようになります。

👉以下の計算機を使用して、負の二項分布に従う変数の確率を計算できます。

負の二項分布の解答済み演習

コインを 8 回投げた場合、8 回目に 4 回目に表が出る確率はどれくらいですか?

まず、コインを投げたときに表が出る確率を計算する必要があります。この場合、考えられる 2 つの結果 (表と裏) のうち、肯定的な結果 (表) は 1 つだけなので、成功の確率は次のようになります。

$p=\cfrac{1}{2}=0,5$

したがって、この問題の確率変数は、r=4 および p=0.5 の負の二項分布に従います。したがって、負の二項分布式を使用して、演習で要求される確率を計算します。

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

負の二項分布の特徴

以下に、負の二項分布の最も重要な特徴を示します。

負の二項分布は 2 つの特性パラメーターによって定義されます。rは望ましい成功結果の数、 pは実行された各ベルヌーイ実験の成功確率です。

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

負の二項分布の分散は、 rに(1-p)を掛けて、 p ²で割った値に等しくなります。

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

パラメーターrが 1 より大きい場合、負の二項分布の最頻値は次の式で計算できます。

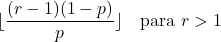
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul> <li>負の二項分布の確率を決定できる質量関数は次のとおりです。</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$